This site is being phased out.
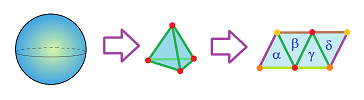
Manifolds
Contents
- 1 What is the topology of the physical Universe?
- 2 The locally Euclidean property
- 3 Two locally Euclidean monstrosities
- 4 The separation axioms
- 5 Manifolds and manifolds with boundary
- 6 The connected sum of surfaces
- 7 Triangulations of manifolds
- 8 Homology of curves and surfaces
- 9 The n-th homology of n-manifolds
- 10 Homology relative to the boundary
What is the topology of the physical Universe?
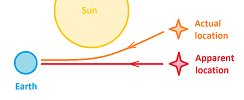
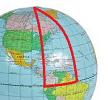
The space of locations of the Newtonian physics is the $3$-dimensional Euclidean space, ${\bf R}^3$. We understand the topology of this space quite well. Most important is that it's acyclic. However, from the point of view of modern physics the universe may be curved. For example, the observation that the light from a star passing the sun deviates from a straight line may be considered as evidence in support of this idea:
But if the universe curves, it might close on itself! Such a space then may have topological features and non-trivial homology groups. Our conclusion is that, locally, the universe looks like ${\bf R}^3$, but possibly not globally.
These “locally Euclidean” spaces are called manifolds.
It may be hard to understand or visualize such a space but, fortunately, we have already made a step in that direction.
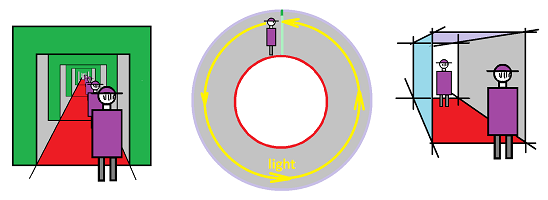
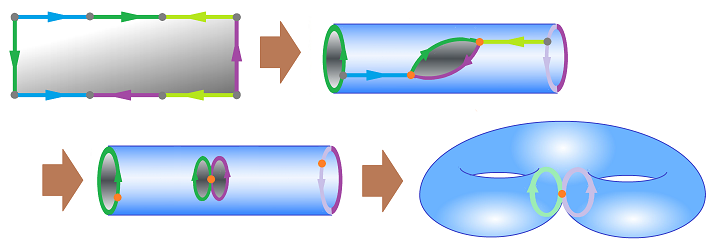
Recall that identifying the front and back walls of a cubical room creates the enfilade effect as light circles this “universe” and comes back to us:
Furthermore, there are still walls present and the light can't go in those directions. Therefore, this can't be a model of the universe. The idea is to take the same cube and glue all three pairs of the opposite faces, one to the other:
This time, there are no walls! The light can propagate in all directions freely. The person can also walk in all directions and his experience will be completely Euclidean. Meanwhile, he sees enfilades of rooms -- with himself in each of them -- in all six directions.
Exercise. Compute the homology of the cube with opposite faces identified and compare it to that of the $3$-sphere.
Note: Why don't we see these copies of ourselves, or the Earth, or the sun, everywhere we look? On a cosmic scale, it takes so long for the light to come back to us that what we see is a distant past. Even the sun is too young to be recognizable or it simply doesn't exist -- there -- yet.
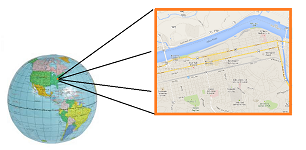
Physics in dimension $2$ makes just as much sense. Let's consider the surface of the Earth as a model. As we look around, this surface appears perfectly flat, just like the plane, ${\bf R}^2$.
How do we even know it's not flat? Over the centuries, there have been a few experiments...
Experiment 1: Eratosthenes computed the difference between the lengths of shadows of the same object at two different locations at the same time of the day. The surface is proven to be curved!
Experiment 2: Magellan showed that one can come back without turning back. That can't be a plane!
Experiment 3: Gauss tried to check if the sum of the angles of a very large triangle (based on three mountain peaks) is equal to $180^o$. Even though the result was inconclusive, the idea was sound. Indeed, this sum is larger than $180^o$ on a sphere! Just consider the triangle formed by two meridians and the equator:
The $1$-dimensional physics is also available and applies to the motion of a car driven along a road or a ball rolling in a ball machine. The difference is that the motion of the ball, unlike that of a car on a road, is governed only by the laws of physics and, as a result, the ball can's make turns at will. This is the reason why, as a model of the universe, these roads and grooves can have no forks or intersections.
This means that they are always, everywhere, simple curves, i.e., curves that locally look like straight lines, ${\bf R}^1$. Once again, we arrive to the idea of a locally Euclidean space. The main examples are the line and the circle.
The locally Euclidean property
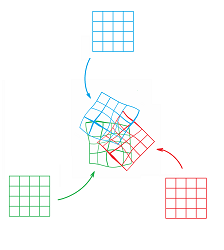
One can think of infinitely many maps that capture a piece of the surface of the Earth. That's why, for the precise definition of the concept we are after, we have to approach the issue from the opposite direction. We are given a (possibly finite) collection of maps/charts and we think of this collection as if it makes up the surface of the Earth. A better metaphor of this idea is the image of patches attached to each other, as in a quilt:
So, these spaces are locally homeomorphic to the Euclidean space of some fixed dimension.
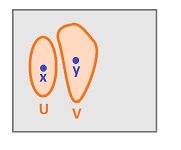
Definition. A topological spaces $X$ is called locally Euclidean of dimension $n$ if for every $x\in X$ there is an open set $U$ such that $x\in U$ and there is a homeomorphism $h:{\bf R}^n \to U$. These homeomorphisms are called charts and any combination of charts that covers the whole $X$ is called an atlas.
Each of these charts creates a local coordinate system for $X$. Such a system provides a locus for the $n$-dimensional linear algebra and calculus.
Of course, “homeomorphic to ${\bf R}^n$” can be replaced with “homeomorphic to an open $n$-ball”, or “box”, etc.:
We start with dimension $1$, and here the charts are simply parametric curves: $$r : (a,b) \to X.$$ In order to ensure that these provide us with homeomorphisms, we need to require the curves to have no self-intersections, i.e., $r(t) \neq r(s)$ for all $a < s < t < b$.
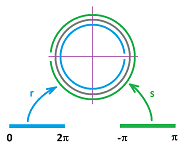
Example (circle). The circle is a very familiar curve and it is normally parametrized with a single function: $$r(t)= (\cos t, \sin t),\ t\in [0,2\pi ].$$ However, $r(0)=r(2\pi)$, which means that this isn't a homeomorphism, even locally. We'll need at least two charts: $$r(t)= (\cos t, \sin t),\ t\in (0,2\pi ),$$ $$s(t)= (\cos t, \sin t),\ t\in (-\pi,\pi ).$$
$\square$
Exercise. Suggest other atlases for the circle.
Exercise. Prove that the figure eight on the plane is not locally Euclidean.
Example (dimension 1). Consider these examples of dimension $1$ locally Euclidean in space. They are closed, open, and half-open; finite and infinite; and the disjoint unions of these:
$\square$
Example (dimension 2). What about dimension $2$? Some of them can be parametrized by a single function:
- the sphere (parametrized by the spherical coordinates),
- the infinite cylinder (parametrized by the cylindrical coordinates), and
- the torus (suggest a parametrization).
Since these functions aren't one-to-one, they aren't charts.
$\square$
Exercise. Sketch an atlas for each of these spaces. Can you make it smaller?
Example (dimension 0). There are $0$-dimensional examples too:
- a point,
- $n$ points,
- ${\bf N} \subset {\bf R}^1$,
- $\{\frac{1}{n} :\ n=1,2,...\}$.
$\square$
Exercise. Prove that $\{0\} \cup \{\frac{1}{n} :\ n=1,2,...\}$ is not locally Euclidean.
Exercise. Prove that in ${\bf R}^N$, the following spaces are locally Euclidean:
- open subsets;
- linear subspaces.
What are their dimensions?
Two locally Euclidean monstrosities
Can all locally Euclidean spaces serve as models of the physical space? The answer is an emphatic No. Some of the locally well-behaved spaces exhibit strange patterns globally.
For the first example, we examine how we handle sequences in ${\bf R}^n$.
The standard basis $\gamma$ of ${\bf R}^n$ is the set of all open $\epsilon$-balls. What if we are interested only in convergence of sequences to a particular point $a\in {\bf R}^n$. Then we would simply consider the standard “local” basis at $a$, which is the set of all open $\epsilon$-balls around $a$:
What's important, however, is that choosing only balls with radii equal to the reciprocals of integers gives us a countable local basis: $$\gamma_a=\{B(a,1/k):\ k=1,2,3,...\}.$$ Limiting our attention to just this collection still allows us to capture sequences convergent to $a$:
Exercise. Prove the above statement.
The reason why this still works is the following local refining property:
Definition. If for every open subset $W$ of $X$ with $a\in W$ there is $U\in \gamma_a$ such that $U\subset W$, then such family is called a local basis of $X$ at $a$.
What about general topological spaces? Recall that a basis of neighborhoods of a topological space $X$ is any family $\gamma$ of subsets of $X$ that satisfies these two axioms:
- (B1) Covering: $\cup \gamma = X$;
- (B2) Refining: for any $U, V\in \gamma$ and any $x\in U\cap V$, there is $W\in \gamma$ with $x\in W$ such that $W \subset U \cap V$.
A basis determines what sets are open in $X$.
Next, for every $a\in X$, we can “localize” the basis $\gamma$ by setting: $$\gamma_a := \{U\in\gamma: a\in U\}.$$
Exercise. Prove that for any (global) basis $\gamma$, its localization $\gamma_a$ is a local basis.
Definition. Spaces that have countable local bases at every point are called first-countable.
Exercise. Prove that every metric space is first-countable.
It follows that every locally Euclidean space is also first-countable.
However, the Euclidean space has an even nicer feature: a countable “global” basis. All it takes is to combine the local countable bases to the ones centered at points with rational coordinates: $$\gamma ' := \cup \{ \gamma _x:\ x=(x_1,...,x_n)\in {\bf R}^n, x_i \in {\bf Q} \}.$$
Exercise. Prove that $\gamma '$ is a basis.
Definition. A space with a countable basis of neighborhoods is called second-countable.
Exercise. Prove that every second-countable space is first-countable. Give a simple example of a space that is first-countable but not second-countable.
Note: A second-countable space is well-behaved in the following sense. It contains a countable, dense subset; that is, there exists a sequence $\{ x_n :\ n=1,2,...\}$ of elements of the space such that every non-empty open subset of the space contains at least one element of the sequence. Such spaces are called separable.
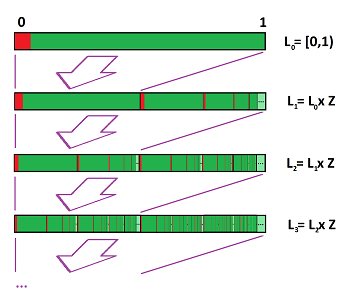
Example. The long line is a topological space similar to the real line ${\bf R}$, but a lot “longer”. While the former consists of a countable number of line segments $[0, 1)$ attached end-to-end, the latter is constructed from an uncountable number of such segments. This is how it is built in a step-by-step fashion:
- First we let $L_0:=[0,1]$;
- then we create countably many copies of $L_0$ and attach to each other end-to-end; informally, $L_1:=L_0\times {\bf Z}$;
- then we create countably many copies of $L_1$ and attach to each other end-to-end; $L_2:=L_1\times {\bf Z}$;
- and so on:
The last step is $$L_{\infty}:=\bigcup_n L_n \setminus \{0\}.$$
Consider a basis of the topology of this space. It has to contain at least one open set from each $[0,1)$, and, therefore, it's uncountable.
$\square$
Note: this space can also be defined via the order topology on ${\bf R}^+ \times [0, 1)$ that comes from the lexicographical order on the set: $(a,b) \le (a',b')$ if and only if $a < a'$ or ($a = a'$ and $b\le b'$).
The key difference between the long line and the Euclidean space is given in the following exercise.
Exercise. Prove that (a) the long line isn't compact yet, (b) every sequence has a convergent subsequence. What about “uncountable” sequences?
Exercise. Prove that for any countable ordinal $\alpha$, pasting together $\alpha$ copies of $[0,1)$ gives a space still homeomorphic to $[0,1)$.
The properties of the long line give an example of what we don't want our model of the physical space to be. This is why in our quest for an intrinsic, purely topological description of this space, we have to require an extra condition: second-countability.
Next, any Euclidean space $X$ satisfies the following condition (more in the next subsection).
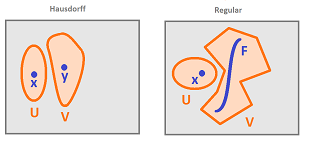
Definition. A space is called Hausdorff if
- any two distinct points have neighborhoods that don't intersect.
In the Euclidean space, it is simple: if $x,y$ are these points in $X$, we choose: $$U := B(x,r),\ V := B(y,r), r := ||x-y||/2.$$
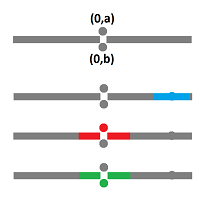
Example. Consider the space called the line with two origins. It is the quotient of two copies of the real line: $${\bf R} \times \{a\} \sqcup {\bf R} \times \{b\},$$ under the following equivalence relation: $$(x,a) \sim (x,b) \text{ if } x \neq 0.$$ The points of this space are:
- $C=[(r,a)]=[(r,b)]$ for each real number $r\ne 0$,
- $A=[(0,a)]$, and
- $B=[(0,b)]$.
In this space, every point has an interval neighborhood:
But also any neighborhood of $A$ intersects any neighborhood of $B$; that's not Hausdorff!
$\square$
This space is so unlike the Euclidean space (globally) that it can't be a model of the physical space and that's why we require an extra condition, Hausdorff.
Thus, we have two pathological examples of locally Euclidean spaces:
- the long line is Hausdorff but not second-countable, while
- the line with two origins is second-countable but not Hausdorff.
Exercise. Prove that
- the long line is Hausdorff, and
- the line with two origins is second-countable.
The separation axioms
The Hausdorff property is an example of a “separation axiom”. Indeed, we separate the two points from each other by means of disjoint open sets:
- for any $x,y \in X, x \neq y$, there are open sets $U, V$ such that $x \in U, y \in V$ and $U \cap V = \emptyset$.
In addition to the Euclidean space, there are a few simple examples of Hausdorff spaces. In the anti-discrete space, we always have $U = V = X$ for non-empty sets, so it's not Hausdorff. In the discrete space, one can always choose $U := \{x \},\ V := \{y \}$, so it's Hausdorff. The real line ${\bf R}$ equipped with the ray topology $\{(p, \infty ) : p \in {\bf R} \}$ isn't Hausdorff because any two rays intersect.
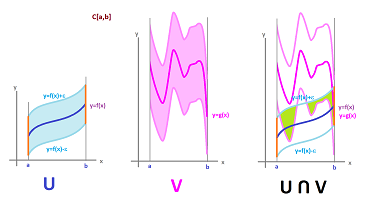
A less trivial example is that of the space of functions with sup-norm.
Exercise. Prove that $C[a,b]$ is Hausdorff. What about $C_p[a,b]$? Or $C(X)$ for some topological space $X$?
Theorem. If $X$ is Hausdorff, then $\{x \}$ is closed for any $x \in X$.
Proof. The idea is to separate $x$ from every other point in $X$. So, if $y \neq x$, then, by definition, there are open sets $U, V$ such that $x \in U, y \in V_y$ and $U \cap V_y = \emptyset$. We don't care about $U$, but we do care that $x$ does not belong to any $V_y$. Then we observe: $$X \setminus \{x \} = \bigcup \{V_y : y \in X \setminus \{x \} \}.$$ This is an open set and, therefore, its complement $\{x \}$ is closed. $\blacksquare$
Exercise. Prove that $X$ is Hausdorff if and only if its diagonal $\Delta:=\{(x,x):x\in X \}$ is closed in $X\times X$.
A higher degree of separation than Hausdorff is when a point and a closed set are separated by neighborhoods:
- for any closed set $F$ and a point $x$ that does not belong to $X$, there are open sets $U, V$ such that $x \in U, F \subset V$ and $U \cap V = \emptyset$.
If, in addition, every singleton $\{x \}$ in $X$ is closed, $X$ is called regular.
Clearly, a discrete space is regular and an anti-discrete is not.
The following is obvious.
Theorem. Every regular space is Hausdorff.
Let's consider the possibility of a converse.
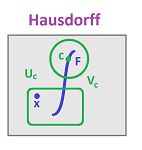
Suppose $X$ is Hausdorff, $F$ is a closed subset of $X$, $x \in X \setminus F$. The idea is to separate $x$ from each $y$ in $F$ and then use these open sets to separate $x$ from the whole $F$. Without jumping to conclusions, let's write down carefully exactly what we've got:
- for any $y \in F$, there are open sets $U_y$, $V_y$ such that $x \in U_Y$, $y \in V_y$ and $U_y \cap V_y = \emptyset$.
How do we build, from these, the two open sets $U,V$ that separate $x$ and $F$?
The first idea is to take the intersections of these sets: $$U:=\bigcap _{y\in F}U_y,\ V:=\bigcap _{y\in F}V_y.$$ Unfortunately, $V$ won't have to include the whole $F$.
The second idea is to try the unions: $$U:=\bigcup _{y\in F}U_y,\ V:=\bigcup _{y\in F}V_y.$$ Unfortunately, $U$ might intersect $F$:
The third idea is to take the intersection for $U$ and the union for $V$. This is something that might work.
Lemma. Given two collections of subsets indexed by the same set: $$\alpha = \{U_y:y \in F\},\ \beta = \{V_y:y \in F\},$$ suppose they are pair-wise disjoint: $$U_y\cap V_y=\emptyset,\ \forall y\in F.$$ Then the sets $$U=\cap \alpha,\ V=\cup \beta,$$ are disjoint too.
Proof. Suppose $z\in U\cap V$. Then
- $z\in U_y$ for all $y\in F$, and
- $z\in V_c$ for some $c\in F$.
Then, $z\in U_c\cap V_c$, a contradiction. $\blacksquare$
This is the outline of the proof:
We are in trouble when we realize that $U$ doesn't have to be open!
Fortunately, an extra assumption of compactness allows us to salvage the proof.
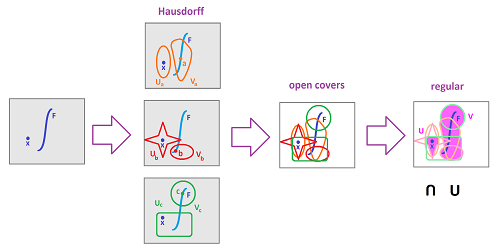
Theorem. A compact space is Hausdorff is and only if it is regular.
Proof. $[\Rightarrow ]$ Suppose $F$ is a closed subset of $X$, $x \in X \setminus F$. Since $X$ is Hausdorff, we have, for any $y \in F$, open sets $U_y$, $V_y$ such that $x \in U_Y$, $y \in V_y$ and $U_y \cap V_y = \emptyset$. Since $X$ is compact and $F$ is closed, $F$ is compact too. Hence the open cover $$\gamma := \{V_y : y \in F \}$$ of $F$ has a finite subcover, $\gamma '$. This means that $$\gamma' = \{V_y : y \in F' \},$$ where $F'$ is a finite subset of $F$. Now define $$U := \bigcap \{U_y : y \in F' \},\ V := \bigcup \{ U_y : y \in F' \}.$$ Both sets are open. And, by the lemma, they are disjoint. $\blacksquare$
This proof is a typical use of compactness...
We just used the following fact: a closed subset of a compact space is compact. A partial converse is contained in the following result.
Theorem. Suppose $X$ is Hausdorff. Then a subset $A$ of $X$ is compact if and only if it is closed.
Exercise. Prove this theorem.
These kinds of extra conditions make it easier to prove topological equivalence by removing the need to verify the requirement that the inverse of the function is to be continuous.
Theorem. Suppose $X$ is compact and $Y$ is Hausdorff. If $f : X \to Y$ is continuous, one-to-one, and onto, then $f$ is a homeomorphism.
Proof. Suppose $A$ is a closed subset of $X$. Then so is $A$. But the image of compact space under a continuous function is a compact too. So, $f(A)$ is a compact subset of $Y$. Since $Y$ is Hausdorff, this implies that $f(A)$ is closed in $Y$. Thus, we have proven that the image of any closed set under $f$ is closed. Hence the preimage of any closed set under the inverse function $f^{-1}$ of $f$ is closed. Therefore, $f^{-1}$ is continuous. $\blacksquare$
Even without being locally Euclidean, a space with the conditions we have considered can be seen as a metric space. We accept the following theorem without proof (see Munkres, Topology. A First Course, p. 216).
Theorem (Urysohn's metrization theorem). Every second-countable, regular space is metrizable, i.e., there is a metric that generates its topology.
Manifolds and manifolds with boundary
Definition. An $n$-dimensional manifold is defined as a topological space that is
- locally Euclidean of dimension $n$,
- second-countable, and
- Hausdorff.
We've used cells as building blocks a lot now, are they manifolds?
No, some of the points -- the ones on the boundary of these cells -- aren't homeomorphic to a Euclidean spaces.
The $1$-cell is the segment $[0,1]$. Here, some of the neighborhoods are open intervals, $V \approx {\bf R}$, and others are half-open intervals, $V \approx {\bf R}_+$ (the half-line).
The same happens in all dimensions. For an $n$-cell $\sigma$, the neighborhoods of the boundary points $\partial \sigma$ are homeomorphic to the half-ball, or to ${\bf R}^n_+ = \{(x_1,...,x_n) : \ x_1 \geq 0\}$, the closed half-space.
Since an $n$-cell is homeomorphic to the closed $n$-ball ${\bf B}^n$, its boundary is homeomorphic to the $(n-1)$-sphere: $$\partial {\bf B}^n \approx {\bf S}^{n-1}.$$
Exercise. Provide the details to prove the above statement.
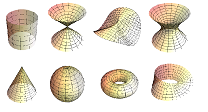
In dimension $2$, manifolds are called surfaces. There are many surfaces around us including the actual manifolds:
But unlike the surface of the Earth or a balloon, these have boundaries.
Definition. A second-countable, Hausdorff space $M$ is called an $n$-manifold with boundary (which might be empty) if for every point $a \in M$, there is an open set (a chart) $U$ such that $a \in U$ and:
- $p : {\bf R}^n \to U$ is a homeomorphism, or
- $p : {\bf R}^n_+ \to U$ is a homeomorphism.
The former points are called the interior, or the inside, points and the latter the boundary points of the manifold. They form the interior, or the inside, $\dot{M}$ and the boundary $\partial M$ of $M$. We will sometimes put the dimension of the manifold as a superscript: $$M=M^n.$$
Note that, if we start with a manifold with non-empty boundary, such as a closed disk, we can remove points from its boundary one by one and acquire a new manifold at every step. In the end of this process, we have a manifold with empty boundary, such as an open disk. All of these manifolds have the same topological features and, therefore, have no independent interest. This is the reason why it is common to concentrate on compact manifolds exclusively.
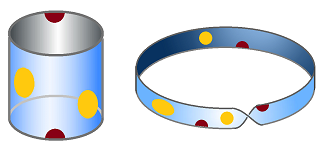
Example. In addition to cells, these are compact manifolds with non-empty boundaries that we have seen:
- the cylinder,
- the Möbius band,
- the cube,
- the cube with one pair of opposite walls identified, etc.
Also, we can create numerous new examples of manifolds by taking any of these or any of the surfaces below and puncture holes or create voids in them.
Exercise. One of the surfaces depicted above isn't a manifold. Which one? What about something that looks like a book?
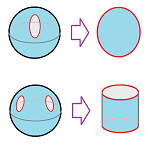
We can deform the sphere with a hole or two (but not more) into something familiar:
Example. We cut a hole in the middle of the projective plane and represent the result as a cell complex with a single $2$-cell. What is it?
$\square$
Exercise. Describe the steps in the above construction.
The $n$-dimensional analog of puncturing a hole in a surface is removing a neighborhood homeomorphic to ${\bf R}^n$ (a void) from an $n$-manifold.
The following is an important result.
Theorem. The boundary of a compact $n$-manifold with boundary $M$ is an compact $(n-1)$-manifold (with empty boundary).
Proof. Each point $x$ in the boundary $\partial M$ of the $n$-manifold $M$ has a neighborhood homeomorphic to the half-space ${\bf R}^n_+=\{(x_1,...,x_n) :\ x_n \geq 0\}$. In fact, $x$ belongs to the image $N_x$ of the boundary of this set, which is the hyperplane, $$N_x \approx {\bf R}^n_0=\{(x_1,...,x_n):\ x_1=0\} \approx {\bf R}^{n-1}.$$ Therefore, $\{N_x:\ x\in \partial M \}$ is an atlas of $\partial M$. $\blacksquare$
Exercise. Provide details for the above proof. Hint: Prove that the boundary $\partial M$ of a compact manifold is a closed subset. Prove that $\dot{M}$ is a manifold (without boundary).
Theorem. The disjoint union of two $n$-manifolds is an $n$ manifold.
Because of this theorem, we concentrate on path-connected manifolds.
Let's apply these results to lower-dimensional manifolds.
Theorem. The only path-connected, compact $1$-manifold is the circle, ${\bf S}^1$.
Also, since $\partial M^1$ is just a collection of points, we have the following:
Theorem. The only path-connected, compact $1$-manifold with non-empty boundary is the closed segment, ${\bf I}$.
While there is only one such $1$-manifold, there is a variety of surfaces. The boundaries of the holes are circles, hence, so are the boundaries of these surfaces. Are all surfaces with boundary like that? We know this is the case for the cylinder and even the Mobius band.
Theorem. The boundary of a compact surface $M^2$ is:
- a closed subset of $M^2$ $\Rightarrow$
- a compact $1$-manifold $N^1$ without boundary $\Rightarrow$
- the disjoint union of a finite number of circles ${\bf S}^1$.
It follows that a surface with boundary can be easily turned into a surface without boundary by attaching a few disks:
Exercise. What happens if you attach the disk to the boundary of the Mobius band? Prove via a diagram.
Exercise. A spider crawls on a surface and leaves a string of its web behind. How can it find out the topology of the surface?
Exercise. One can create $3$-manifolds by “thickening” graphs. Explain exactly how it is done.
The connected sum of surfaces
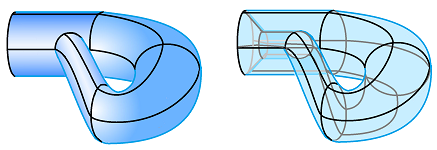
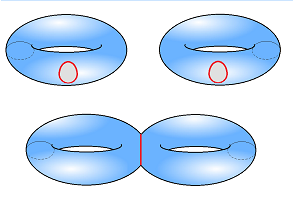
Any two surfaces can be attached to each other by puncturing holes in them and then gluing them together along these edges. The result is called the connected sum $S_1 \# S_2$ of surfaces $S_1,S_2$.
For example, this is how you create the double torus by attaching two tori to each other in this fashion:
More precisely, suppose $N_i$ is a subset of $S_i$ for $i=1,2$ homeomorphic to a disk, then its boundary is homeomorphic to a circle: $$N_i\approx {\bf B}^2,\ \partial N_i\approx {\bf S}^1 .$$ Then we define $$S_1 \# S_2 := \Big[ (S_1 \setminus N_1) \sqcup (S_2 \setminus N_2) \Big] / _{\sim},$$ where the equivalence relation is generated by a homeomorphism $$h:\partial N_1 \to \partial N_2 .$$
We can illustrate the process via these gluing diagrams:
One can also interpret the diagram by gluing along the edges:
Exercise. Prove $S \# {\bf S}^2 = S$.
Exercise. What is ${\bf P}^2 \# {\bf P}^2$?
Exercise. Prove $$H_1({\bf T}^2\#{\bf T}^2) = {\bf R}^3 .$$
Exercise. Suppose $K_1,K_2$ are simplicial complexes the realizations of which are surfaces: $$|K_i|=S_i,\ i=1,2.$$
- (a) Define a complex $K$ such that $|K|=S_1 \# S_2$ (in other words, find a triangulation of the connected sum in terms of those for the two surfaces). Hint: don't cut cells.
- (b) Express the homology of $K$ in terms of the homology of $K_1,K_2$:
$$H_1(K)= H_1(K_1) \ ? \ H_1(K_2).$$
The construction allows one to classify all surfaces as in the theorem below that we will accept without proof (see Kinsey, Topology of Surfaces, p. 81).
Theorem (Classification of surfaces). (1) A compact path-connected surface is homeomorphic to
- the sphere ${\bf S}^2$, or
- the connected sum of $n$ tori ${\bf T}^2$, or
- the connected sum of $n$ projective planes ${\bf P}^2$.
(2) These options are not homeomorphic.
Therefore, the options are: ${\bf S}^2, \ n{\bf T}^2, \ n{\bf P}^2$.
Exercise. Classify:
- ${\bf S}^2 \# {\bf S}^2,$
- ${\bf P}^2 \# {\bf K}^2,$
- ${\bf T}^2 \# {\bf K}^2,$
- ${\bf K}^2 \# {\bf K}^2.$
Exercise. Classify all $1$-manifolds with an analog of connected sum.
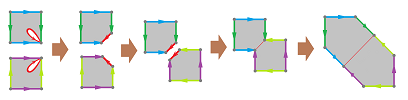
Let's consider what happens to the Euler characteristic when we form the connected sum of two tori. Based on the above diagram, cutting the disks out has the following consequences:
- no new faces, net effect $0$;
- one new, shared edge, net effect $-1$;
- one existing vertex becomes shared, net effect $-1$.
Thus, the net effect is $-2$.
This argument applies to all surfaces:
Theorem. For two surfaces $S$ and $T$, $$\chi(S \# T) = \chi(S) + \chi(T) - 2.$$
Exercise. Use the formula to compute the Euler characteristic of the $n$-torus.
Triangulations of manifolds
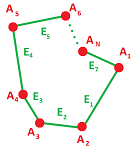
Next, we study manifolds represented by data; given a simplicial complex $K$, what are the necessary and sufficient conditions that its realization $|K|$ is an $n$-manifold $M^n$ (without boundary)? When this is the case, we will call $K$ a combinatorial $n$-manifold.
First, let's take care of the point-set topological issues. Since the realization is the union of finitely many $n$-balls and, therefore, second-countable, then so is $|K|$. For Hausdorff, two points are in either the same cell, which is Hausdorff, or in two disjoint stars, which serve as the required disjoint neighborhoods.
Exercise. Provide the details of this proof.
So, we only need to deal with the question whether $|K|$ is locally Euclidean: every point in $M^n$ has a neighborhood homeomorphic to ${\bf R}^n$.
The first observation is simple.
Theorem. If $|K|\approx M^n$ then $\dim K =n$.
Now, suppose we have an $n$-dimensional simplicial complex $K$. How do we know that $K$ is a combinatorial $n$-manifold? Can we answer this question just by examining the list of simplices of $K$? The answer is Yes.
We start with dimension $n=1$. We could use the two “global” results from the above, but instead we start from the definition. First, by the above theorem, $K$ has to be a graph. Since the star of a vertex with more than one adjacent edge isn't homeomorphic to the open interval, we have to require that there are exactly two:
- each vertex is shared by exactly two edges.
The condition can be restated in terms of vertices only.
Theorem. A graph $K$ is a combinatorial $1$-manifold if and only if the following condition is satisfied:
- (A1) if $A\in K$ then there are exactly two vertices $P,Q\in K$ satisfying $AP, AQ\in K$.
Next, dimension $n=2$. The first requirement a complex has to satisfy to be a surface is similar to the one above:
- each edge is shared by exactly two faces.
Just as the last one, this condition can fail in two ways:
- an edge is contained in exactly one face,
- an edge is shared by more than two faces.
In the first case, we have, possibly, a surface with boundary. In the second, a point on this edge does not have a neighborhood homeomorphic to the open disk.
Exercise. To justify the above statement, prove that three copies of ${\bf R}^n_+$ glued together by the hyperplane $\{x_1=0\}$ is not homeomorphic to ${\bf R}^n$. Hint: same as idea as in the proof that “T” isn't homeomorphic to “I”.
Now, we restate this condition combinatorially, i.e., for a $2$-dimensional simplicial complex $K$ given by a list vertices and simplices as sets of vertices: $$K=\{A,B,C,...,AB,BC,...,ABC,...\}.$$ In terms of these sets, every face is a triple, such as $ABC$, and every edge is a double, such as $AB$. The above condition can then be restated in terms $K$ as:
- (A2) if edge $AB\in K$ then there are exactly two vertices $P,Q\in K$ satisfying $ABP, ABQ \in K$.
This condition does not guarantee that the realization of $K$ is a surface, as the image below shows.
Indeed, condition (A2) is satisfied here for all edges but the vertex in the middle does not have a neighborhood homeomorphic to the disk.
Exercise. To justify the above statement, prove that two copies of ${\bf R}^n$ glued together by the origin $0$ is not homeomorphic to ${\bf R}^n$.
Then, we have to require that the faces around each vertex are arranged in, and can be listed as, a circular fashion to form a disk-like subcomplex.
Given a vertex $A$ the faces (triangles) that contain $A$ have to form a “cycle”:
We can state this as a condition on faces:
- For each vertex $A$, suppose
- all edges that contain $A$ are $E_1, E_2, ..., E_k$, and
- all triangles that contain $A$ are $T_1, T_2, ..., T_m$.
- Then $k=m$ and the two sets can be re-indexed in such a way that:
- $E_1$ is shared by $T_1, T_2$;
- $E_2$ is shared by $T_2, T_3$;
- ...
- $E_m$ is shared by $T_m, T_1$.
Of course, we recognize this collection of simplices as the star of vertex $A$.
Restated in terms of subsets of $K=\{A, B, C, ...\}$, the above condition will take the following form:
- (B2) for each vertex $A\in K$, the set $\{ B\in K: AB \in K \}$ can be represented as $\{B_1, B_1, ..., B_m\}$ with
$$AB_1B_2, AB_2B_3, ..., AB_mB_1 \in K.$$
Theorem. A $2$-dimensional simplicial complex $K$ is a combinatorial $2$-manifold if and only if it satisfies conditions (A2) and (B2).
Exercise. Is this a triangulation of the projective plane?
Exercise. Prove an analog of the above theorem for manifolds with boundary.
The reason why we impose these conditions on a complex is clear now: we have to check that the star of every simplex of every dimension forms an $n$-ball. The difficulty is that there will be $n$ of such conditions and we will have to set them up one at a time for each dimension from $0$ to $n$. Let's consider just one of them.
In light of our discussion of conditions (A1) and (A2), the simplest way things can go wrong is when three pieces that are already homeomorphic to the $n$-ball are glued to each other. In other words, if an $(n-1)$-simplex is shared by three $n$-simplices, this is not an $n$-manifold.
Condition (A3) is illustrated below:
Unlike the theorem above for $n=2$, the next one gives us only a necessary condition.
Theorem. If $K$ is a combinatorial $n$-manifold then $K$ satisfies the following condition:
- (A$n$) if $A_0A_1...A_{n-1}\in K$ then there are exactly two vertices $P,Q\in K$ satisfying $A_0A_1 ...A_{n-1}P\in K$ and $A_0A_1 ...A_{n-1}Q\in K $.
What conditions (A1),(A2), ...,(A$n$) have in common is not the dimensions of these cells but rather their codimensions: $$\operatorname{codim} \sigma:=n-\dim \sigma.$$ These conditions are about cells of codimension $1$.
Exercise. Suggest condition (B3) and illustrate it with a sketch. Hint: What's the codimension?
Exercise. Give an example of a simplicial complex that satisfies conditions (A3) and (B3) but is not a combinatorial $3$-manifold.
Homology of curves and surfaces
From the discussion of the local issues in the last subsection, we move on to the global issues.
Suppose $K$ is a combinatorial $n$-manifold which is path-connected. What do we know about the homology of $K$?
Let's list the results that we have established so far. Since there are no cells of dimension above $n$ in the manifold, we conclude that $$H_k(K)=0,\ k>n.$$ Then we only need to consider $H_k(K)$ for $k=0,1,...,n$. We group the results as follows.
Group 1, the $0$ dimension:
- $H_0(K) = {\bf Z}$ for any $K$.
Group 2, the intermediate dimensions:
- $H_1({\bf S}^2) = 0$;
- $H_1({\bf T}^2) = {\bf Z} \times {\bf Z}$;
- $H_1({\bf K}^2) = {\bf Z}\times {\bf Z}_2$;
- $H_k({\bf S}^n) = 0$ for $0 < k < n$.
Group 3, the $n$th dimension:
- $H_1({\bf S}^1) = {\bf Z}$;
- $H_2({\bf S}^2) = H_2({\bf T}^2) = {\bf Z}$;
- $H_2({\bf K}^2) = H_2({\bf P}^2) = 0$;
- $H_n({\bf S}^n) = {\bf Z}$.
Let's be clear here and make an important point: the formulas in Groups 2 and 3 are the result of computations of homology for several specific representations of these topological spaces as simplicial and cell complexes. Meanwhile, the formula in Group 1 was proved as a theorem independent from representations. Our goal in this subsection is a similar theorem for Group 3.
We see only two outcomes in Group 3: $0$ and ${\bf Z}$. Let's try to explain what's going on.
As we know, $H_2(K)$ is determined by whether $|K|$ has a void in it. In other words, it is whether this surface holds air inside. If it does, there is one side of the surface that touches the air while the other doesn't. Such surfaces are called orientable; for example, the sphere and the torus. Otherwise, a surface is called non-orientable. In that case the surface doesn't separate inside from the outside; for example, the Klein bottle and the projective plane. The reason is that, as we have seen, these surfaces contain the one-sided Mobius band.
Below we will concentrate on the orientable case.
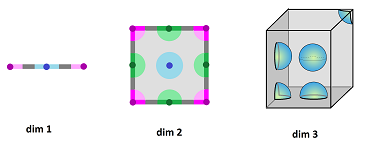
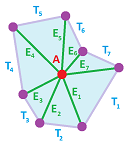
Let's consider the sphere. In the case of the simplest cell complex, the void is captured by the single $2$-cell, as a cycle. In the case of the simplest simplicial complex, it is the sum of all of its four $2$-cells:
Hence the idea: the $2$-homology is generated by the sum of all $2$-cells of the sphere: $$H_2=< \alpha +\beta +\gamma +\delta >.$$ The broader idea is that the $n$-th homology group of an $n$-manifold may be generated by the sum of all of its $n$-cells. The question is though, what should be signs (and the orientations) of these cells in the sum?
To see how we can handle this issue, we start with dimension $n=1$. We will work combinatorially, with the simplicial complex $K$ the realization of which is the $1$-manifold $M$. Then $M$ is supposed to be the circle.
Suppose we have an edge $A_1A_2\in K$. Then, by condition (A1) from the last subsection applied to vertex $A_2$, there is exactly one vertex $A_3 \in K$ such that $A_2A_3\in K$. We do the same for vertex $A_3$ next and then continue by induction. Since $K$ is finite, this process will have to start to repeat itself. Also, since $K$ is path-connected, the list of its vertices will then be exhausted. Therefore, there is an integer $N$ such that
- $A_1,...,A_N$ is the list of all vertices of $K$, and
- $A_1A_2,..., A_{N-1}A_N, A_NA_1 \in K$.
Thus, we have a circular sequence of edges and vertices:
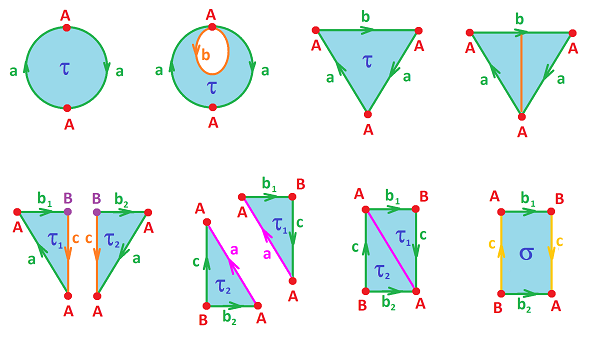
Let $$\tau := A_1A_2 + ... + A_{N-1}A_N + A_NA_1 .$$ Then $$\begin{array}{lll} \partial \tau &= \partial (A_1A_2) + ... + \partial (A_{N-1}A_N) + \partial (A_NA_1) \\ &=(A_2 - A_1)+(A_3-A_2)+... +(A_N-A_{N-1})+(A_1-A_N) \\ &=0. \end{array}$$ What happened here? All vertices in the boundary of $\tau$ cancelled because each appeared twice, with $+$ and with $-$. Therefore, $\tau$ is a cycle. For convenience, we add $A_{N+1}=A_1$ to the list; then we have $$\tau = \sum _{i=1}^{N} s_i A_iA_{i+1}.$$
Now, something we could have overlooked, if we hadn't been expecting to see it, is that choosing $A_1A_2,..., A_{N-1}A_N,\ A_NA_1 \in K$ amounts to choosing an orientation of all $1$-cells in $K$, which becomes an oriented simplicial complex. The way the orientations are chosen is to satisfy this “cancellation property”:
- two edges that share a vertex induce opposite orientations on that vertex.
Theorem. If $K$ is a combinatorial path-connected $1$-manifold, then $$H_1(K)=< \tau > = {\bf Z}.$$
Proof. What's left to be proven? We need to find the rest of the $1$-cycles. Suppose $\sigma$ is one. Then $$\sigma = \sum _{i=1}^{N} s_i A_iA_{i+1},$$ for some $s_i\in {\bf Z}$. Then, $$\begin{array}{lll} \partial \sigma &= \sum _{i=1}^{N} s_i \partial (A_iA_{i+1}),\\ & = \sum _{i=1}^{N} s_i (A_{i+1} - A_i)\\ & =\sum _{i=1}^{N} (s_{i+1}-s_i) A_i \\ &= 0? \end{array}$$ Since $A_i \ne 0$, in order to produce zero, the coefficients have to vanish: $s_i=s_{i+1}$. Therefore, $s_i=s$ for all $i$. Hence $$\begin{array}{lll} \sigma &= \sum _{i=1}^{N} s A_iA_{i+1},\\ &=s \sum _{i=1}^{N+1} A_iA_{i+1}\\ &=s \tau \in < \tau > \end{array}$$ $\blacksquare$
The result is certainly familiar, but this is the first time it is proven to be independent from the realization.
Now, we are after the generator $O_K$ of the $n$-th homology group of a combinatorial $n$-manifold $K$: $$H_n(K)= < O_K >.$$ When this generator is non-zero, it is called the fundamental class of $K$. What possible lessons about it have we learned from the case of dimension $1$?
- (1) The candidate for the fundamental class is the sum of all $n$-cells in $K$, provided they are oriented according to the “cancellation rule”:
- (2) Two $n$-cells that share an $(n-1)$-cell induce opposite orientations on that cell. Such an orientation is called compatible and the procedure for finding one is based on the following:
- (3) selecting an orientation for a single $n$-cell dictates the orientations of all the rest.
If a compatible orientations exists for all cells, the manifold is called orientable.
Exercise. Use the above approach to prove $H_n({\bf S}^n;\ {\bf Z}_2)={\bf Z}_2$.
We next apply this approach to the case $n=2$.
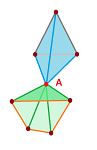
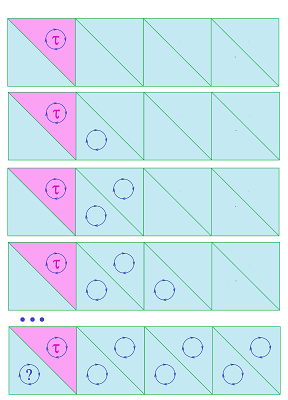
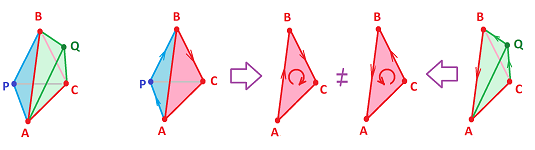
We can choose compatible orientations, as long as we deal with one edge at a time:
But, can we ensure that all pairs of faces have compatible orientations? We proceed as follows. Start with an oriented face $\tau$. Then, suppose $\tau$ has an edge $d$ shared with face $\lambda$. Then $\lambda$ is given the orientation compatible with that of ${\tau}$. Next, $\lambda$ has an edge $f$ shared with another face which has to have the compatible orientation with $\lambda$, etc. At every step, we move from a face to an adjacent face and every time the orientation of the next face is “forced”. This may continue for a while:
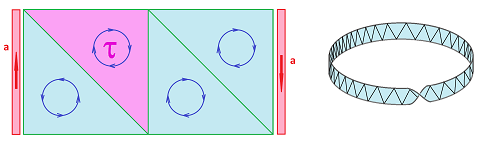
But what happens if we make a full circle and come back to ${\tau}$? It's possible that the orientation to be imposed on ${\tau}$ from the last face will be opposite of what we have already. The last line above suggests how this can happen: the strip of faces we follow may have finished a full flip when we come back. In other words, we have the Mobius band inside:
Meanwhile, this four-cell triangulation of the sphere is OK:
Exercise. Show that there is no compatible orientation of the Mobius band ${\bf M}^2$, regardless of the triangulation. Prove that a surface is orientable if and only if it doesn't contain (an embedded copy of) ${\bf M}^2$.
Exercise. Prove that for a non-orientable path-connected compact combinatorial surface $K$, $H_2(K) = 0$. Hint: the construction is the same as above: propagation of coefficients of faces in the decomposition of a $2$-cycle.
The n-th homology of n-manifolds
The two low dimensions we have considered so far are special:
- dimension $1$: all manifolds are orientable;
- dimension $2$: non-orientability is detected by the presence of the Mobius band.
Let's recall that, in general, an orientation of a simplex is a particular way of listing its vertices. The given orientation of a simplex is passed along to its faces by dropping one of the vertices from the ordered list:
Once orientability is understood, the proof is very similar to the case of dimension $1$. Let's just follow the algebra.
As a combinatorial $n$-manifold $K$ has no $(n+1)$-cells, its $n$-boundary group is trivial: $$B_n(K) = \partial (C_{n+1}(K)) = \partial(0) = 0.$$ Therefore, we only need to compute the $n$-cycle group: $$H_n(K) = Z_n(K) / B_n(K) = Z_n(K) / 0 = Z_n(K).$$
Suppose $C$ is a non-zero $n$-cycle and $$C := \displaystyle\sum_s d_s s,\ d_s \in {\bf Z},$$ with summation over all $n$-cells $s$ in $K$. What do we know about these numbers?
Since $C$ is a cycle, the boundary $\partial C$ of $C$ is zero: $$\partial C = 0,$$ or $$\partial C = \displaystyle\sum_s d_s \partial s = 0.$$ Since this is the sum of $(n-1)$-cells in an $n$-manifold, we can use condition (A$n$): every $(n-1)$-cell is shared by exactly two $n$-cells. Therefore, every $(n-1)$-cell $e$ appears exactly twice in the above sum. Since $\partial C = 0$, every $(n-1)$-cell $e$ has to cancel. We have the following:
Lemma 1. If $(n-1)$-cell $e$ is shared by $n$-cells $\sigma$ and $\tau$ then $$d_{\sigma} = \pm d_{\tau}.$$
Since $K$ is path-connected, one can get from $s$ to any other face by following edge-face-edge-face... sequence. By applying Lemma 1 inductively, we obtain the following:
Lemma 2. For any two $n$-cells $\sigma$ and $\tau$ in $K$, $$d_{\sigma} = \pm d_{\tau}.$$
Which sign? We have to look at the orientations of these cells. For example, suppose $n$-cells $\sigma, \tau$ share $(n-1)$-cell $e$. Then they have orientations that generate the opposite orientations on $e$. Otherwise, $$\begin{array}{ll} C &= \sigma + \tau + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} \sigma, \tau \Rightarrow \\ \partial C &= e + e + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e \\ &\neq 0, \end{array}$$ because $e \neq 0$. This is the conclusion.
Lemma 3. Suppose $C$ is a non-zero $n$-cycle in an orientable path-connected combinatorial $n$-manifold $K$ and $$C = \displaystyle\sum_s d_s s,\ d_s \in {\bf Z},$$ over all $n$-cells $s$ in $K$. Then for any two faces $\sigma$ and $\tau$ in $K$, we have $$d_{\sigma} = d_{\tau}.$$
It follows that $$C = d \displaystyle\sum_s s,$$ for some real $d$. We have proven the following:
Theorem. Suppose $K$ is an orientable path-connected combinatorial $n$-manifold. Then the $n$-th homology group of $K$ is generated by the fundamental class, $$H_n(K) = < O_K > \cong {\bf Z},$$ which is the sum of all $n$-cells in $K$ compatibly oriented: $$O_K:=\displaystyle\sum_s s.$$
Theorem. Suppose $K$ is a non-orientable path-connected combinatorial $n$-manifold. Then the $n$-th homology group of $K$ is trivial: $$H_n(K) = 0.$$
Exercise. Prove the theorem. Hint: use the lemmas above.
Homology relative to the boundary
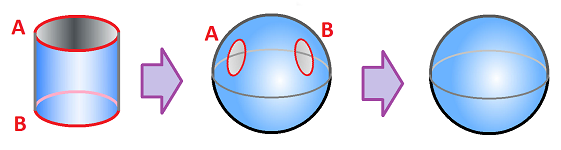
But what if $K$ has boundary? We know that the formula doesn't hold anymore; after all, the cylinder can't hold air. Or can it? It can if we patch its holes! Patching the two holes turns the cylinder into a surface without boundary. This surface, the sphere, can hold air:
To appreciate this observation, compare this to patching the hole of the Möbius band. The result is the projective plane that can't hold air. This means that the homology of the “patched” version of the manifold is just as interesting as that of the original! The $n$-th homology is, in fact, more interesting because it tells us when the manifold is orientable.
The patching of a surface can be accomplished, topologically, by adding disks to cover the holes or by collapsing each hole to a point, one at a time.
Exercise. Suggest a procedure for patching holes in a combinatorial surface.
It's not as simple for a general combinatorial $n$-manifold $K$. We need to collapse each path-component of the boundary $\partial K$ to a point. This collapse creates an equivalence relation on $K$. Is this still a simplicial complex?
Exercise. Give an example when it's not.
Instead of dealing with this issue, we adopt a purely algebraic approach. We construct the quotients of the chain groups: $$C_k(K,\partial K):= C_k(K) / _{\sim}.$$ The homology is then computed via the quotients of the boundary operators: $$[\partial _k]: C_k(K,\partial K) \to C_{k-1}(K,\partial K).$$ The result is called the relative homology with respect to the boundary and is denoted by $H(K,\partial K)$.
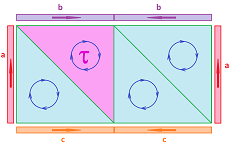
Example. Let's compute $H({\bf B}^2,{\bf S}^1)$, the homology of the disk relative to its boundary.
The complex $K$ of the disk is:
- $0$-cell: $A$;
- $1$-cell: $a$;
- $2$-cell: ${\tau}$;
- boundary operator: $\partial (\tau) = a; \partial (a) = 0$.
We create the relative chain complex by identifying the $1$-cell with $0$. This creates the quotients of the chain groups of $K$: $$\begin{array}{llll} C_2(K,\partial K)&=C_2(K) / _{\sim} &= < \tau >;\\ C_1(K,\partial K)&=C_{1}(K) / _{\sim} &= < a > / < a > = 0;\\ C_0(K,\partial K)&=C_0(K) / _{\sim} &= < A > . \end{array}$$
This is what relative $1$-cycles look like:
Then the quotients of the boundary operators and groups form a chain complex and we compute its homology: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccc} & & < \tau > & \ra{[\partial _2]=0} & 0 & \ra{[\partial _1]=0} & < A >\\ {\rm kernels:} & & Z_2 = < \tau > && Z_{1} = 0 & & Z_{0} = < A > \\ {\rm images:} & & B_2 = 0 && B_{1} = 0 & & B_{0} = 0 \\ {\rm quotients:}& & H_2 = < \tau > \cong {\bf Z} && H_{1} = 0 & & H_{0} = < A > \cong {\bf Z} \end{array}$$ Both the chain complex and the homology groups coincide with those of the sphere, as expected.
$\square$
Exercise. Provide such a homology computation for the Mobius band.
Exercise. Prove that $\{C(K,\partial K),[\partial ]\}$ is a chain complex.