This site is being phased out.
Motion planning in robotics
Redirect to:
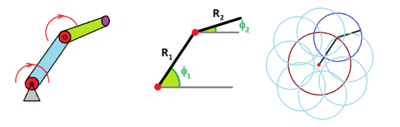
A robotic arm with a single joint is parametrized by a curve: $$x=R\cos \theta, y=0, z=R\sin\theta,$$ where $\theta$ is the angle of the rod and $R$ is the length of the arm.
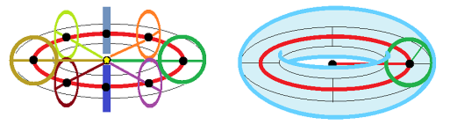
Now, the configuration space of a two-joint arm is the torus: $${\bf T}^2={\bf S}^1 \times {\bf S}^1 .$$
It is parametrized by $$x=R_1\cos \theta_1 + R_2 \cos\theta_2, y=0, z=R_1\sin \theta_1 + R_2 \sin\theta_2,$$ where $\theta_1,\theta_2$ are the angles of the two arms and $R_1,R_2$ are the lengths of the arms. Under the assumption $R_1>R_2$, the operational space is the annulus.
Now, since these functions are periodic, they can be seen as a function from the torus to the space.
It is an example of the forward kinematics map, i.e., the map from its configuration space to the operational space that associates a location of the end of the arm to each configuration.
Exercise. A telescoping arm with a joint has the cylinder: $${\bf C}^2=[0,1] \times {\bf S}^1 $$ as the configuration space. Find its forward kinematic map.
The forward kinematics map can be used for motion planning.
By looking at its homology map one can learn about the possible behavior of the robot under various circumstances.
For example, in the above example of a 2-joint arm, the forward kinematic map is given as $$f:{\bf T}^2 \to A,$$ where $A$ is the annulus. Whatever the exact map is, its homology map $$f_*:H_1({\bf T}^2)={\bf R}\times{\bf R} \to H_1(A)={\bf R}$$ can be easily analyzed. It's the projection. Indeed, $H_1({\bf T}^2)={\bf R}\times{\bf R}$ is generated by the two joints but only the first one is mapped to the the generator of $H_1(A)={\bf R}$. The second joint does not allow to go around the annulus and, therefore, its homology class collapses under $f$. This wouldn't be the case if $R_1<R_2$, but then the homology of the operational space is trivial.
It is important to notice that the homology maps are the same for all maps homotopic to $f$. Therefore, the results are stable under perturbations and noise. For more see Lefschetz numbers and controllability.
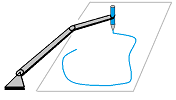
One can use this information to try to match the configuration space with a possible operational space such as when one uses a given robot arm design to spray paint a topologically complex surface: $$f:{\bf T}^n={\bf S}^1 \times ... \times {\bf S}^1 \times {\bf S}^2 \to S.$$ The analysis of possible homology maps between the homology groups of these manifolds will help to rule out some designs.
Exercise. Find all possible homology maps for the robot above with $S={\bf S}^2$ and $S={\bf T}^2$.
For this "3d" two-joint arm:
with the rods (first red, second green) perpendicular to each other, the configuration space and the operational space are homeomorphic via the obvious forward kinematic map. It's homology map is the identity.
Suppose the end of the arm is to follow a particular path in the operational space, then one needs to find how the configuration parameters are to be changed for this to happen. This is called the inverse kinematic problem.
More precisely, given a continuous path $p:[0,1] \to A$, in the the operational space, find a path $q:[0,1] \to C$, in the configuration space, such that $p=fq$, where $f$ is the forward kinematic map.
If, in addition, we assume that these paths are loops, the existence of a solution for this problem ("solvability", "well-posedness") is studied via the maps of the fundamental group as $p=f_*(q)$.
Exercise. Find all possible maps of the fundamental groups for the robot above with $S={\bf S}^2$ and $S={\bf T}^2$.
From the geometric point of view one looks at the derivative of this map $$f':TC \to TA,$$ which operates between the tangent bundles of these manifolds. Singularities of this map, i.e., the points where the derivative has zero determinant, will indicate potential problems with the design. The reason is that in this case the Implicit Function Theorem can't guarantee that $f$ is locally a diffeomorphism. Because of that the inverse kinematic problem doesn't always have a solution.
For the configuration space of $n$ particles/robots in space $M$: $$C=M^n -\Delta,$$ where $$\Delta=\{(u_1,...,u_n)\in M^n: u_i = u_j\},$$ the first question of motion planning is, is it possible to reach all configurations? In other words, is $C$ path-connected?