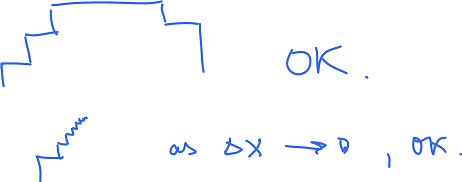This site is being phased out.
Isotropy in numerical PDEs
Contents
Problems with isotropy in numerical PDEs
Recall...
Heat equation $$\frac{\partial T}{\partial t}=-k\nabla^{2} T.$$
Wave equation $$\frac{\partial^2 F}{\partial t^2} = c^2 \nabla^2 F.$$
Finite differences
The idea of the finite differences method of solving PDEs is that, given a number of "discretization points", nodes, one assigns one unknown per point, and writes one equation per point. At each point, the derivatives of the unknown are replaced by finite differences via Taylor series of the functions. When solved these equation produce recurrence relations that we use to update the state of the simulation.
The method is based on a square grid.
In dimension 2, the recurrence relations are...
Heat equation:
$T_{ t+\Delta t}^{(x,y)} - T_{t}^{(x,y)} =$
$ \hspace{30 pt} -k \frac{\Delta t}{\Delta x^2} \Big[ (T_{t}^{(x,y)}-T_{t}^{(x,y-\Delta y)})+(T_{t}^{(x,y)} - T_{t}^{(x,y+\Delta y)})+(T_{t}^{(x,y)}-T_{t}^{(x-\Delta x,y)})+(T_{t}^{(x,y)}-T_{t}^{(x+\Delta x,y)})\Big].$
Wave equation:
$F^{(x, y)}_{t+\Delta t} - 2F^{(x, y)}_{t} + F^{(x, y)}_{ t-\Delta t} =$
$ \hspace{30 pt} c^2 \frac{\Delta t^2}{\Delta x^2} \Big[ (F^{(x+\Delta x, y)}_{t} F^{(x, y)}_{t})+ (F^{(x- \Delta x, y)}_{t} - F^{(x, y)}_{t})+ (F^{(x, y+\Delta y)}_{t} - F^{(x, y)}_{t})+ (F^{(x, y-\Delta y)}_{t} - F^{(x, y)}_{t}) \Big].$
(Assume $\Delta x = \Delta y$.)
LGCAs also has a recurrence/update formula...
Convergence
The solutions should converge to the solution of the PDE (a word used for this is "mimetic"), or at least to something.
Symbolically: $$||u_n-u|| \rightarrow 0.$$ However, the norm might vary.
Whatever $u$ is, it is expected to be isotropic in the real world. So, the lack of isotropy when it is preserved under the refinements of the grid indicates the lack of convergence.
Convergence conditions
Observe that a single grid can't be expected to produce an isotropic solution. A sequence is needed.
There are analytical conditions that guarantee convergence.
For the heat equation, in two dimensions, $$k \frac{\Delta t}{\Delta x^2} \leq 1/4.$$ For the wave equation, in two dimensions, $$c \frac{\Delta t^2}{\Delta x^2} \leq 1/2.$$
In the latter case, if the condition isn't satisfied, one can see how a circular wave grows corners...
So, as we refine our discretization we have to make sure that the condition is satisfied.
So, the conditions give the discretization schemes that are acceptable.
However, the finite difference method becomes justify in more complex situations.
- First, the coefficients involved in the equation may be location- (e.g. in the case of heterogeneous media) or time-dependent.
- Second, adding damping or other linear and non-linear terms required by more realistic scenarios could make the above analysis impossible.
As a result, we won't know ahead of time what discretization schemes are acceptable.
Other grids
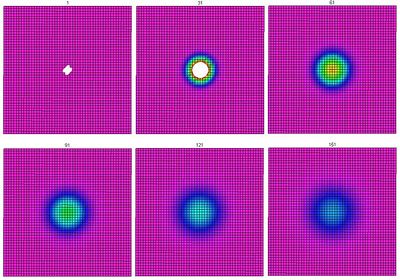
The heat equation has been thoroughly studied for describing how heat disperses itself through continuous media. It is well known that in a homogeneous medium, the spread of heat should be isotropic.
Sometimes we don't get to choose the discretization but can only refine it.
In discretizing the heat equation, the idea is that the change in temperature of a 2-cell is directly proportional to the difference between its temperature and the temperature of adjacent 2-cells. The main conclusion is that the isotropy of heat on a grid is heavily dependent upon the geometry of the grid. (Modeling with discrete exterior calculus)
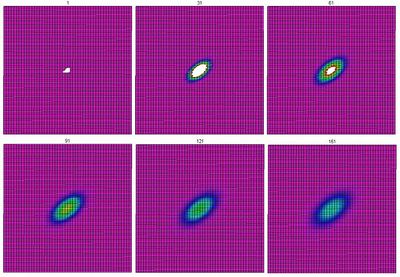
For example, the square grid and the rhomboidal grid are topologically identical, but heat spreads isotropically through one and not through the other:
Altogether:
- heat equation:
- regular grids are OK,
- rhombus and other with less symmetry aren't;
- wave equation: similar;
- LGCAs:
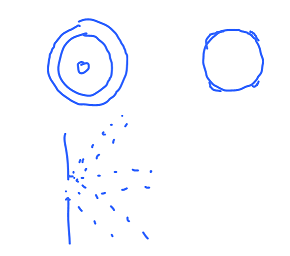
- anisotropy is obvious for a square grid,
- for hexagonal grid anisotropy of the flow becomes visible at high speeds.
Conclusions
Not all discretizations are acceptable for a given (physical) problem.
Which ones are OK depends on the relation of certain parameters:
- the conductivity $k$ for the heat equation,
- the spring constant $c$ for the wave equation,
- the flow speed for LGCA,
to
- the grid/lattice/mesh, and/or
- the discretization parameters $\Delta t, \Delta x$.
As an example this is how we numerically analyze the heat equation:
Given $c$ ----> analysis ---> find acceptable $\Delta t, \Delta x$ ---> simulation
However, the analytical part might not even exits for some realistic situations.
The isotropy problem elsewhere
A much simpler problem..
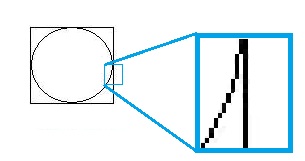
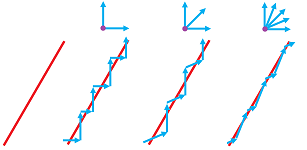
Suppose we discretized the plane with the square grid and we want to compute lengths of curves based on their approximations by digital curves.
Observation: The perimeters of a square and the inscribed circle are the same:
Indeed, it takes exactly as many vertical (and horizontal) steps to get from the left end of the circle to the top - no matter whether you make just one turn or many. (Not surprising as this square is a circle, with respect to the taxicab metric.) Therefore, $\pi=4$! (the circumference of the circle divided by twice the radius).
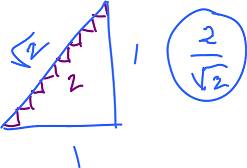
A simpler example comes from our attempt to compute the length of diagonal:
The relative error is the same, $2/\sqrt 2$ even though $\Delta x \rightarrow 0$.
The problem is further explored in paper On Local Definitions of Length of Digital Curves [1] by Mohamed Tajine and Alain Daurat. One breaks a digital curve into a sequence of “small” ($n$ steps) curves, each small curve is assigned a length (it does not have to be the distance from the beginning to the end), then the length of the original curve is the sum of those. As the resolution, $\Delta x$, approaches $0$, the length computed this way should converge to the “true” length but it does not no matter what scheme you have chosen and the relative error remains the same.
To explain why... Once $n$ is chosen, the number of possible angles that curves of $n$ steps can generate is finite. Meanwhile slopes of segments run (continuously!) from $0$ to $360$ degrees. No matter how large $n$ is, there will be whole intervals of possible slopes missed. So the problem is that no grid is non-isotropic.
Just like with the numerical PDEs, some problems can be solved. Some curves are OK to approximate this way while some are not:
So, we have to match the discretization to the problem via analytical study. We can't go straight to approximation.
Again: not all discretizations are acceptable for a given problem.
Analysis
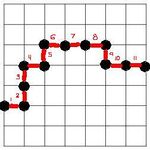
These are possible angles from the grid:
We can always find an angle that isn't there. In fact, since there are only finitely many of them, there is always some separation and that's why the relative error remains the same no matter what $\Delta x$ is.
Solution: make sure that the set of all possible angles is getting denser and denser.
More generally, this can be interpreted as a problem of computing lengths of curves in cell complexes:
- a curve == a sequence of edges == 1-chain,
- its length == the sum of the lengths of the edges == the arc-length integral over the $1$-chain.
We have
- a sequence of complexes $K_1,...,K_n,...,$
and it produces:
- a sequence of sets of vertices $V_1,...,V_n,...,$
- a sequence of sets of edges $E_1,...,E_n,...$
Note: In the setup above (PDEs and length), all complexes are cubical complexes. Also, for the length problem only $1$-skeletons matter.
Given a curve $L$, there is one $L_n$ in each complex that approximates $L$. So, does the sequence converge, to $L$?
In general, the diameter of the mesh is defined as: $$\Delta x _n = max_ {x \in V_n} min_{y \in V_n} d(x,y).$$
We have $$\Delta x_n \rightarrow 0.$$
One takes best approximations of the curve and considers whether:
- they converge to $L$, and
- their lengths converge to the length of $L$.
Yes on the first one, but only with respect to the max norm. The derivatives don't converge (and remember the derivative does appear in the arc-length formula). So, this is a no in fact and it's a no on the second one too.
So, no convergence of lengths without convergence of derivatives, i.e., slopes!
Conclusion: we need isotropy.
Define $$\Delta \alpha_n = max_ {a \in E_n} min_{b \in E_n} \angle (a,b).$$
So, what if: $$\Delta \alpha_n \rightarrow 0?$$
Solution?
Discretization with "asymptotic" isotropy?
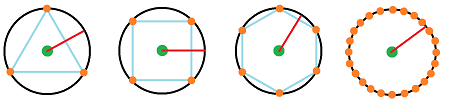
Possibilities:
- combination of several rotated square grids,
- union of straight lines with angles $\{ k \cdot \pi /n: k=0,...,n-1\}$;
- random grid,
- increasing density and
- Delaunay triangulation,
- barycentric subdivision;
- the average of several rotated square grids(*).
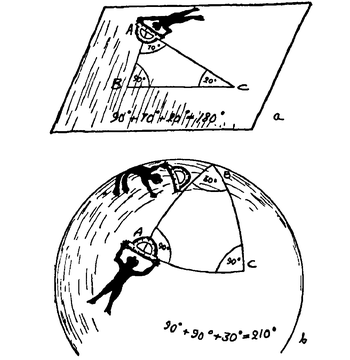
Deeper reason: curved space?
As the image below suggests, the discretization of the plane makes it curved.
We check the Euclidean theorem:
- the sum of the angles in a triangle == $\pi$.
On the square grid, the sum of the angles is larger than 180 degrees. Therefore, it has a sphere-like (positive curvature) geometry.
A similar issue will arise when you compute the surface area.