This site is being phased out.
Wave equation
The PDE of wave propagation
Just as before, we will provide the mathematics to describe the following three parts of the setup:
- the topology of the cell complex $L$ of the objects and springs,
- the geometry given to that complex such as the lengths of the springs, and
- the physics represented by the parameters of the system such as those of the objects and springs.
Let $u(t,x)$ be the function that measures the displacement from the equilibrium of the object associated with position $x$ at time $t$ (we will suppress $t$). It is an algebraic quantity: $$u=u(t,x)\in R \times R.$$ As such, it can represent quantities of any nature that may have nothing to do with a system of objects and springs; it could be a wave in a liquid:
Here, the particles of the liquid are vertically displaced while waves propagate horizontally (or we can see the pressure or stress vary in a solid medium producing sound).
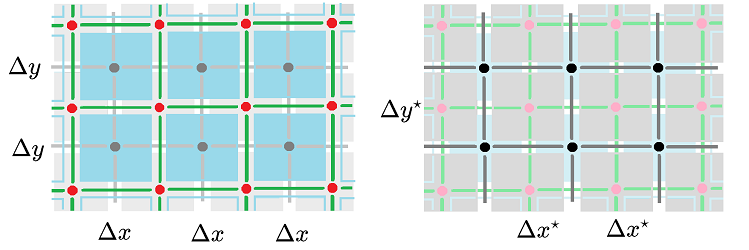
First, we consider the spatial variable, $x\in {\bf Z}\times {\bf Z}$. We think of the array -- at rest -- as the standard $2$-dimensional cubical complex $L={\mathbb R}^2$. The complex may be given a geometry: each object has a (possibly variable) distances $\Delta x, \Delta y$ to its neighbors and the distance between the centers of the springs has length $\Delta x^\star, \Delta y^\star$. We think of $u$ as a form of degree $0$ -- with respect to $x,y$.
According to Hooke's law, the force exerted by the spring is $$F_{Hooke} = -k df,$$ where $df\in R$ is the displacement of the end of the spring from its equilibrium state and the constant, stiffness, $k\in R$ reflects the physical properties of the spring. If this is the spring that connects locations $x$ and $x+1$, its displacement is the difference of the displacements of the two objects. In other words, we have: $$df=u(x+1) - u(x).$$ Therefore, the force of this spring is $$H_{x,x+1} = k \Big[ u(x+1) - u(x) \Big].$$ Since $k$ can be location-dependent, it is a $1$-form over $L$.
Note that for a constant $k$, we are dealing with the second derivative of the $0$-form $u$ with respect to space:
$$u' '=\star d_x\star d_xu = \Delta u.$$
Compare it to the second derivative of a $1$-form $U$ with respect to space:
$$U' '=d_x\star d_x\star U = \Delta U,$$
which we used to model $1$-dimensional diffusion. The difference is seen in the two different starting points in the same Hodge duality diagram:
$$
\newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!}
\newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.}
\newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!}
\newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.}
%
\begin{array}{ccccccccccc}
u\in & C ^0({\mathbb R}^2) \ & \ra{d_x} & C ^1({\mathbb R}^2) &\ni U \\
& \ua{\star} & \ne & \da{\star} \\
& C ^1({\mathbb R}^2^\star) \ & \la{d_x} & C ^0({\mathbb R}^2^\star)\\
\end{array}
$$
Then,
$$d_xu' ' = (d_xu)' '.$$
Second, we consider the temporal variable, $t\in {\bf Z}$. We think of time as the standard $1$-dimensional cubical complex ${\mathbb R}_t$. The complex is also given a geometry. It is natural to assume that the geometry has no curvature, but each increment of time may have a different duration (and, possibly, $\Delta t \ne \Delta t^\star$). We think of $u$ as a form of degree $0$ with respect to $t$.
Now suppose that each object has mass $m$. Then, by the Second Newton's Law, the total force is $$F=m \cdot a,$$ where $a$ is the acceleration. It is the second derivative with respect to time, i.e., this $0$-form: $$a=u_{tt}:=\star d_t \star d_t u . $$ The mass $m$ is a $0$-form too and so is $F$. Note that the stiffness $k$ is also a $0$-form with respect to time.
Now, with these two forces being equal, we have derived the wave equation of differential forms: $$\begin{array}{|c|} \hline \\ \quad m u_{tt} = (k^\star u_x)_x. \quad \\ \\ \hline \end{array}$$
If $k$ and $m$ are constant forms (and $R$ is a field), the wave equation takes a familiar shape: $$u_{tt}=\tfrac{k}{m}u_{xx}.$$
Exercise. Derive the dual (with respect to space) wave PDE.
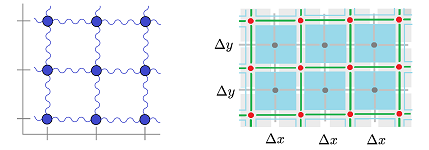
We next consider an array of objects connected by springs, both vertical and horizontal:
The forces exerted on the object at location $x$ are the four forces of the four springs attached to it: $$\begin{array}{llll} H & = H_{x,x-1} + H_{x,x+1} + H_{y,y-1} + H_{y,y+1}\\ & = k[ u(x-1,y) - u(x,y) ] \\ & + k[ u(x+1,y) - u(x,y) ] \\ & + k[ u(x,y-1) - u(x,y) ] \\ & + k[ u(x,y+1) - u(x,y) ] . \end{array}$$
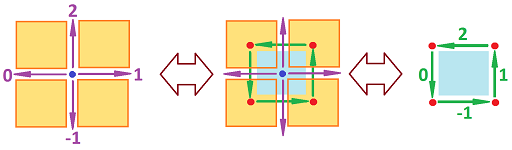
We still consider only $0$- and $1$-forms but on the standard $2$-dimensional cubical complex $L={\mathbb R}^2$. Hodge duality is slightly more complicated here. As an example, these are a $1$-form $\varphi$ and its dual $1$-form $\varphi^*$:
Just as in the $1$-dimensional case, each bracketed term in the expression for $F$ is the exterior derivative: two with respect to $x$ and two with respect to $y$: $$\begin{array}{llll} k[ u(x-1,y) - u(x,y) ] &= kd_xu([x,x-1],y), \\ k[ u(x+1,y) - u(x,y) ] &= kd_xu([x,x+1],y), \\ k[ u(x,y-1) - u(x,y) ] &= kd_yu(x,[y,y-1]),\\ k[ u(x,y+1) - u(x,y) ] &= kd_yu(x,[y,y+1]). \end{array}$$ We can rearrange these terms as they all start from $(x,y)$: $$H= kdu\left\{\begin{array}{llll} & & +\{x\}\times [y,y+1] \\ &+[x,x-1]\times \{y\} & & +[x,x+1]\times \{y\}\\ & & +\{x\}\times [y,y-1] \end{array}\right\},$$ where $d=(d_x,d_y)$. To get the duals of these edges, we just rotate them counterclockwise. Then, $$H= kd^\star u\left\{\begin{array}{llll} & & +[x^+,x^-]\times \{y^+\} \\ &+\{x^-\}\times[y^+,y^-] & & +\{x^+\}\times[y^-,y^+]\\ & & +[x^-,x^+]\times \{y^-\} \end{array}\right\},$$ where “$^\pm$” stands for “$\pm 1/2$”.
Observe that the dual edges are aligned counterclockwise along the boundary of the square neighborhood $[x^-,x^+]\times [y^-,y^+]$ of the point $(x,y)$. That neighborhood is the Hodge dual of this point. We recognize this expression as a line integral: $$H= \displaystyle\int_{\partial (\star (x,y))} \star kdu.$$
Now by the Stokes Theorem, the integral is equal to: $$H= \star d_x \star kd_xu .$$ Since the left-hand side is the same as before, we have the same wave equation: $$m u_{tt} = (k^\star u_x)_x.$$
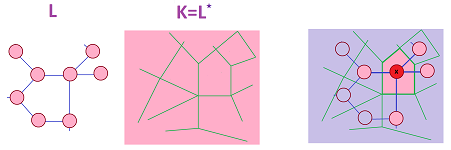
In general, the medium may be non-uniform and anisotropic, such as wood:
We model the medium with a graph of springs and objects with a possibly non-trivial geometry:
We are now in the same place as with the diffusion equation. We split the data into three categories:
- 1. the adjacency of the springs (and the objects) is the topology,
- 2. the lengths of the springs (and the angles and the areas of their cross-sections) is the geometry, and
- 3. the Hooke's constants of the springs is the physics. $\\$
They are given by, respectively:
- 1. the cell complex $L$,
- 2. the Hodge star operator $\star^m :C^m(L)\to C^{n-m}(L^\star)$, and
- 3. the primal $1$-form $k\in C^1(L)$.
The two complexes dual to each other are shown below:
The total force that affects the object located at vertex $x$ in $L$ is $$F= \star \displaystyle\int_{\partial (\star x)} \star kdu.$$ Therefore, we end up with the same wave equation as above. Its right-hand side is seen as the full circle in the Hodge duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} u\in & C ^0(L) & \ra{\quad d_x \quad} & C ^1(L) & \\ &\quad\quad \quad\ua{\times\frac{|a^0|}{|b^n|}} & \ne & \quad\da{\times\frac{|b^{n-1}|}{|a^1|}} \\ & C ^n(L^\star)& \la{\quad d_x \quad} & C ^{n-1}(L^\star),\\ \end{array} $$ where $a$ and $b$ are dual.
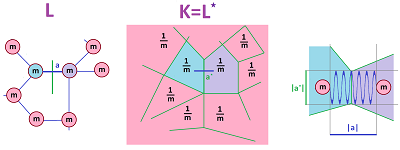
The geometry of the primal complex $L$ is given first by the lengths of the springs. What geometry should we give to the dual complex $K=L^\star$?
First, the meaning of the coefficients of the Hodge star operator are revealed to be represented by the stiffness $k(a)$ of spring $a$. In fact, it is known to be directly proportional to its cross-sectional area $|b|$ and inversely proportional to its length $|a|$: $$k(a):=E\frac {|b|} {|a|},$$ where $E$ is the “elastic modulus” of the spring. Plainly, when the angles are right, we have simply $b=a^\star$.
Second, we assign the reciprocals of the masses to be the $n$-volumes of the dual $n$-cells: $$|x^\star|:=\frac{1}{m(x)}.$$
Then we have the simplified -- with the physics taken care of by the geometry -- wave equation, $$u_{tt}=(E^\star u_{x})_x,$$ where $E$ is the $1$-form of elasticity. Its right-hand side is seen as the full circle in the Hodge duality diagram modified accordingly: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} u\in & C ^0(L) & \ra{\quad d_x \quad} & C ^{1}(L) & \\ &\quad\quad \quad\ua{\times\frac{1}{m(b^n)}} & \ne & \quad\da{\times k(a^1)} \\ & C ^n(L^\star)& \la{\quad d_x \quad} & C ^{n-1}(L^\star)\\ \end{array} $$
Next we simulate wave propagation with a spreadsheet. The $2$-dimensional case is treated with the formula given above. This is the result of a circular wave with a single source bouncing off the walls of a square box.
Exercise. Implement the wave illustrated on the first page of this chapter.
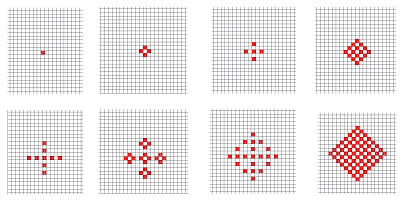
Example. The choice of $$K={\mathbb R}^2,\quad R={\bf Z}_2,$$ produces this simple “cellular automaton”:
$\square$