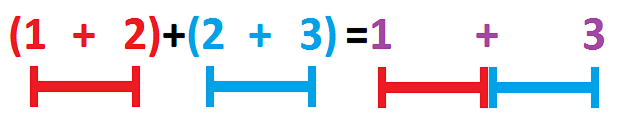This site is being phased out.
Introduction to discrete calculus
Contents
- 1 Domain ${\mathbb R}$
- 2 The boundary operator
- 3 Cochains as linear functions
- 4 The derivative of a $0$-cochain is a $1$-cochain
- 5 Algebraic properties of the exterior derivative
- 6 The Fundamental Theorem of Calculus
- 7 The geometry of ${\mathbb R}$
- 8 The derivative as the rate of change
- 9 The second derivative of a $0$-cochain
- 10 Newtonian physics, the discrete version
Domain ${\mathbb R}$
We next examine the combined domain of these new functions.
We are to make the usual domain of functions -- the reals ${\bf R}$ -- discrete. We divide this set into unit intervals:
The result is a collection of both edges and vertices:
- a node, or a $0$-cell, is $\{n\}$ with $n=...-2,-1,0,1,2,3, ...$;
- an edge, or a $1$-cell, is $[n, n + 1]$ with $n=...-2,-1,0,1,2,3, ...$. $\\$
These two collections are the domains of $0$- and $1$-cochains respectively.
For convenience, we will use the following notation:
- $A$ for the name of the node (i.e., $A$ is an integer), and
- $AB$ for the edge (i.e., nodes $A$ and $B$ are consecutive integers).
We will denote the collection of all these items by: $${\mathbb R}:=\big\{ A:\ A=...-2,-1,0,1,2,3, ...\big\} \cup \big\{AB:\ A=...-2,-1,0,1,2,3, ..., B=A+1\big\}.$$
This change of notation (from ${\bf R}$ to ${\mathbb R}$) is meant to underscore the fact that:
- there is no algebra of numbers anymore, and
- there is only topology of edges attached to each other.
In fact,
- $1$-cells are attached to each other along $0$-cells.
This key point is understood by considering how the boundaries are formed.
The boundary of an edge is the union of its endpoints: $$\partial (AB)=A\cup B.$$ However, we will treat it algebraically, as the sum of its endpoints: $$\partial (AB)=A+B.$$ The main idea then is:
More precisely,
Now, what about boundaries of more complex objects? They are still made of cells and we simply think of them, again, as formal sums of cells, chains. For the empty set, we reserve a special chain: we adopt the convention that
Further, we need to combine their boundaries somehow to form the boundary of the object.
Suppose we have two consecutive edges in ${\mathbb R}$. They share a common node in the middle. This node is special. In the combined boundary of the chain,
- it appears twice, but
- it shouldn't appear at all! $\\$
It is supposed to cancel!
Now algebraically, suppose the edges $AB$ and $BC$ are in ${\mathbb R}$. Then: $$\partial(AB+BC)=\partial(AB)+\partial(BC)=(A+B)+(B+C)=A+(B+B)+C=?=A+C$$ Then $B+B$ has to be $0$.
Thus, this algebraic rule of cancellation should apply: $$2x = 0.$$ In other words, if a cell appears twice, it is canceled. The computation is carried out as if we do algebra with binary arithmetic. That's why we can think of our chains both as finite “combinations” and as finite binary sums of cells. The latter idea is preferable: $$a = \displaystyle\sum_i s_i \sigma_i,\ s_i =0 \text{ or } 1.$$ Then, as the boundary operator is defined on each of the cells, we can now extend this definition to all $1$-chains: $$\partial(a) := \displaystyle\sum_i s_i \partial( \sigma_i ),$$ subject to the cancellation rule.
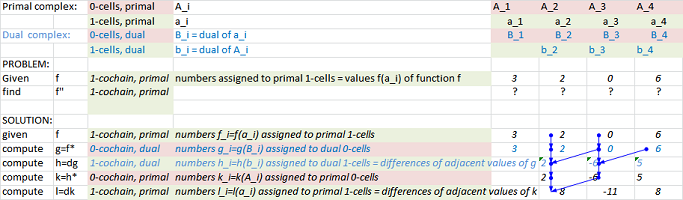
Cells can be presented in a spreadsheet such as Excel. Below, some of the rows and columns are narrowed in order to emphasize the $1$-dimensional nature of the edges and the $0$-dimensional nature of the vertices.
Also, the coordinates differ from those in the above discussion by a factor of two:
- $0$-cells are odd, and
- $1$-cells are even.
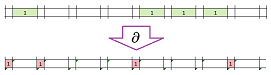
The chains are encoded by putting $0$s and $1$s in all cells. In the former case, the cell is white and the number is invisible while in the latter case, the cell is colored according to its dimension.
Next, we implement the boundary operator.
These are the results of computing boundaries, for a $1$-chain (green):
The approach to the algorithm for computing the boundary operator is very different from the algebra we have done. Compare the following.
- Normally, to compute the boundary of a $1$-chain, we evaluate the boundary of each of its $1$-cells as the sum of this cell's boundary cells (dimension $0$), add them, and then cancel the repetitions.
- Now, we look at either $0$-cell present in the spreadsheet, add the values of the $1$-cells of the chain adjacent to it, and then find out whether the result makes this cell a part of the boundary of the chain. $\\$
The results are of course the same.
The code is very simple. For each node, we compute the sum, modulo $2$, of the values at the two edges adjacent to it: $$\texttt{ = MOD( RC[-21] + RC[-19], 2)}$$ Then the result is placed on the right. It follows that,
- if the chain isn't there, we have $0+0=0$;
- if the chain is passing through, we have $1+1=0$;
- if the chain ends here, we have $1+0=1$.
Link to file: Spreadsheets.
The boundary operator
Under this approach however we have $AB=BA$... These edges can't serve as domains of integration as explained in the last subsection.
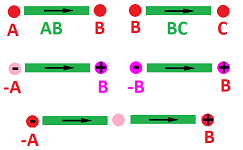
We define chains as linear combinations of edges: $$a = \displaystyle\sum_i s_i \sigma_i,\ s_i \in {\bf R} ,$$ with real coefficients. These edges are oriented: $$BA=-AB.$$
But what about the boundaries? The middle node in the boundary of $AB+BC$ won't cancel as it did above. We will have to change the definition of the boundary.
We know that the boundary of a edge $AB$ should be a linear combination of its two endpoints $A$ and $B$, but what are the coefficients? What helps here is that we, again, expect the boundary of $AB+BC$ to be a linear combination of $A$ and $C$, so $B$ has to cancel: $$\begin{array}{lll} ?A+?C&=\partial (AB+BC)&=\partial (AB)+\partial (BC)\\ &=(?A+?B)+(?B+?C)&=?A+(?B+?B)+?C. \end{array}$$ Therefore, $B$ has to appear with the opposite signs! For example, it might be “$+$” in $\partial (AB)$ and “$-$” in $\partial (BC)$. But the only difference between them is the position of $B$ with respect to the direction of these edges, the beginning or the end.
Definition. The boundary of an edge is equal to its final node minus the initial node; i.e., $$\partial (AB) := B-A.$$
Furthermore, the boundary of the chain above is $$\partial(a) := \displaystyle\sum_i s_i \partial( \sigma_i ).$$
Definition. For $k=0,1$, we define the $k$th chain group $C_k({\mathbb R})$ of ${\mathbb R}$ as the set of all $k$-chains in ${\mathbb R}$.
Suppose ${\mathbb R}$ has the set of nodes $N$ and the set of edges $E $. Then the two chain groups are the linear combinations of the nodes and edges respectively: $$\begin{array}{lllll} C_0({\mathbb R})&:=\Big\{\displaystyle\sum s_i A_i: A \in N,\ s_i\in {\bf R} \Big\} ,\\ C_1({\mathbb R})&:=\Big\{\displaystyle\sum r_i a_i: a_i \in E,\ r_i\in {\bf R} \Big\} . \end{array}$$ These are two vector spaces with their basis served by $N$ and $E$ respectively.
So, the boundaries of $1$-cells are $0$-chains, and, moreover, the boundaries of $1$-chains are $0$-chains as well. Then, boundaries are found by the function defined above: $$\partial : C_{1}({\mathbb R}) \to C_{0}({\mathbb R}).$$ It is called the boundary operator.
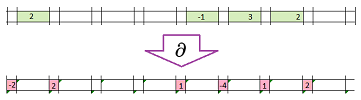
The code is almost the same. For each node, we compute the difference of the values at the two edges adjacent to it: $$\texttt{ = -RC[-21] + RC[-19]}$$
Link to file: Spreadsheets.
Cochains as linear functions
As explained above, we think initially of a $k$-cochain as a real-valued function defined on $k$-cells of ${\mathbb R}$.
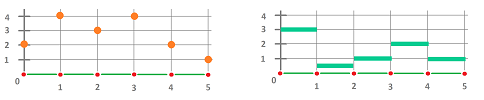
This is how we plot the graphs of cochains in ${\mathbb R}$:
To emphasize the nature of a cochain as a function, we can use arrows:
Here we have two cochains:
- a $0$-cochain with $0\mapsto 2,\ 1\mapsto 4,\ 2\mapsto 3, ...$; and
- a $1$-cochain with $[0,1]\mapsto 3,\ [1,2]\mapsto .5,\ [2,3]\mapsto 1, ...$.
A more compact way to visualize is this:
Here we have two cochains:
- a $0$-cochain $Q$ with $Q(0)=2,\ Q(1)=4,\ Q(2)=3, ...$; and
- a $1$-cochain $s$ with $s\Big([0,1] \Big)=3,\ s\Big([1,2] \Big)=.5,\ s\Big([2,3] \Big)=1, ...$.
We can also use letters to label the cells, just as before. Each cell is then assigned two symbols: one is its name (a latter) and the other is the value of the cochain at that location (a number):
Here we have:
- $Q(A)=2,\ Q(B)=4,\ Q(C)=3, ...$;
- $s(AB)=3,\ s(BC)=.5,\ s(CD)=1, ...$.
Thus, we think of $0$-cochains as simple discrete functions. Then one of the familiar theorem from calculus holds.
Theorem (Intermediate Value Theorem). Given a $0$-cochain $f$, if $$f(A)<c<f(B)$$ for some nodes $A,B$ and some $c\in{\bf R}$, then there is a edge $A'B'$ located between the nodes $A,B$ and $t\in [0,1]$ such that $$c=(1-t)f(A')+tf(B').$$
We next show that we can think of $1$-cochains as definite integrals.
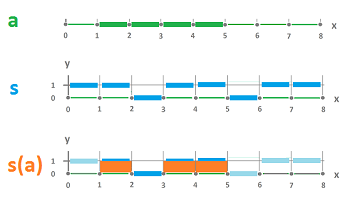
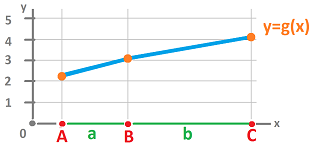
Example. Let's consider a very simple example:
- $a$, a chain equal to the sum of the edges from $1$ to $5$, and
- $s$, a cochain with its $1$ and $0$ values shown.
Notice that for $a$ the edges other than the four can be ignored, while $s$ is defined everywhere. What does this have to so with the area under the graph of $s$ over $a$?
Algebraically, we have a chain, $$a=[1,2]+[2,3]+[3,4]+[4,5],$$ while $s$ is known only for the single edges: $$s\Big( [0,1]\Big)=1,\ s\Big([1,2]\Big)=1,\ s\Big([2,3]\Big)=0,\ ...$$ To get from here to the values of the area, we need first to extend $s$, as a function, from single edges to their combinations, $1$-chains. Second, we need additivity of $s$ as a function: $$\begin{array}{lllll} s(a)&=s\Big( [1,2]+[2,3]+[3,4]+[4,5] \Big)\\ &=s\Big( [1,2]\Big)+s\Big([2,3]\Big)+s\Big([3,4]\Big)+s\Big([4,5]\Big)\\ &=1+0+1+1\\ &=3. \end{array}$$ $\square$
Thus, $s(a)$ is the area of the graph of $s$ that lies over $a$ as well as the displacement of an object that moves with speed given by $s$ over a period of time represented by $a$. The notation so justified is: $$s(a)= \displaystyle\int_a s, \quad \text{ or } s(AB)= \displaystyle\int_A^B s.$$
It comes with counterparts of the properties of the Riemann integral:
- additivity:
$$\int\limits_{[a,b]} s +\int\limits_{[c,d]} s = \int\limits_{[a,b]+[c,d]} s;$$
- orientation:
$$\int\limits_{-[a,b]} s = -\int\limits_{[a,b]} s,$$
- scalar multiplication:
$$\int\limits_{r[a,b]} \sigma = r\int\limits_{[a,b]} \sigma.$$
Example. The last property allows us to extend the above computation to arbitrary chains. Indeed, the coefficients of the edges in $a$ can take any real numbers, for example: $$a=2\cdot [1,2]+(-1)\cdot [2,3]+0\cdot [3,4]+ [4,5].$$ Suppose also $$s\Big([1,2]\Big)=3,\ s\Big([2,3]\Big)=0,\ s\Big([3,4]\Big)=-1,\ s\Big([4,5]\Big)=1.$$ We compute using these properties: $$\begin{array}{lllll} s(a)&=s\Big( 2\cdot [1,2]+(-1)\cdot [2,3]+0\cdot [3,4]+\pi\cdot [4,5] \Big)\\ &=2\cdot s\Big( [1,2]\Big)+(-1)\cdot s\Big([2,3]\Big)+0\cdot s\Big([3,4]\Big)+ s\Big([4,5] \Big)\\ &=2\cdot 3+(-1)\cdot 0+0\cdot (-1)+ 1 \\ &=7. \end{array}$$ This is still the area under the graph of $s$ but with some of the edges appearing more than once. $\square$
As we see, only the values of the cochain on the edges (and the linearity) is required for this computation.
These three properties are combined into one,
- linearity:
$$\int\limits_{r[a,b]+t[c,d]} s = r\int\limits_{[a,b]} s +t\int\limits_{[c,d]} s .$$
To summarize, $1$-cochain were originally refined on edges only and now they are defined on all $1$-chains. Because of linearity, however, the former fully determines the latter. Furthermore, without referring to integrals for justification, $0$-cochains are also subjected to this generalization.
Definition. A cochain of degree $k=0,1$, or simply a $k$-cochain, is a linear function $s:C_k({\mathbb R})\to {\bf R}$; i.e., for all $r,t\in{\bf R}$ and all $a,b\in C_k({\mathbb R})$, we have: $$s(r\cdot a+t\cdot b)=rs(a)+ts(b).$$
Separately, we write for nodes and edges: $$s(r\cdot A+t\cdot B)=r\cdot s(A)+t\cdot s(B) ,\ A,B\in {\mathbb R}, $$ and $$s(r\cdot AB+t\cdot CD)=r\cdot s(AB)+t\cdot s(CD) ,\ AB,CD\in {\mathbb R}.$$
The set of $k$-cochains is denoted by $C^k({\mathbb R})$.
Cochains can be represented as tables, see Spreadsheets. They can also be represented by formulas. In either case, only the values of the cochain on the cells are provided. For example, these are $0$-chains: $$f(n)=3n^2+1,\ g(n)=\sin n,\ h(n)=2^n, \text{ etc. }$$ The formulas are understood as real numbers assigned to each node $n=...,-2,-1,0,1,2,...$. The rest of the values are found from this data via linearity. For example, $$f(2n+5m)=2f(n)+5f(m)=2(3n^2+1)+5(3m^2+1)=6n^2+15m^2+7.$$ Similarly, we only provide the values for $1$-cochains on the edges: $$s\big( [n,n+1] \big)=3n^2+n-7, \text{ etc. }$$
Thus, $1$-cochains can be integrated and, in fact, they are integrals. Next, what calculus is associated with $0$-cochains?
The derivative of a $0$-cochain is a $1$-cochain
Even though we are familiar with the derivative of a function as the rate of change, the change will be initially our interest.
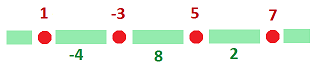
The functions we are dealing with are discrete. At their simplest, they are defined on the integers: $$A=...-1,0,2,3,4, ....$$ These are $0$-cochains, they change abruptly and, consequently, the change is simply the difference of values: $$f(A+1)-f(A).$$ The only question is where to assign this number as the value of some new function. What is the nature of the input of this function?
The illustration below suggests the answer:
The output should be assigned to the (oriented) edge $AB$: $$AB \mapsto f(B)-f(A).$$ Assigning this number to either of the two endpoints would violate the symmetry of the situation. If the input changes in the opposite way, so does the change of the output, as expected: $$BA=-AB \mapsto f(A)-f(B).$$
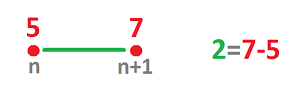
Example. Let's look at this construction from the point of view of our study of motion. Suppose function $p$ gives the position and suppose
- at time $n$ hours we are at the $5$ mile mark: $p(n)=5$, and then
- at time $n+1$ hours we are at the $7$ mile mark: $p(n+1)=7$. $\\$
We don't know what exactly has happened during this hour but the simplest assumption would be that we have been walking at a constant speed of $2$ miles per hour. Now, instead of our velocity function $v$ assigning this value to each instant of time during this period, it is assigned to the whole interval: $$v\Big( [n,n+1] \Big)=2.$$ This way, the elements of the domain of the velocity function are the edges. $\square$
The relation between a discrete function and its change is illustrated below:
Definition. The exterior derivative of a discrete function $f$ at $AB$ is defined to be the number $$(df) \big(AB \big):=f(B)-f(A).$$
Thus, we have:
- $f$ is defined on the $0$-cells, and
- $df$ is defined on $1$-cells.
Definition. The exterior derivative $df$ of a $0$-cochain $f$ is a $1$-cochain $df$ given on each interval by the above formula.
The exterior derivatives can be computed for $0$-cochains given by tables, see Spreadsheets. When they are represented by formulas, the computations are straightforward: $$f(n)=3n^2+1\ \Longrightarrow\ (df)\big( [n,n+1] \big)=(3(n+1)^2+1)-(3n^2+1)=6n+3;$$ $$g(n)=\frac{1}{n}\ \Longrightarrow\ (dg)\big( [n,n+1] \big)= \frac{1}{n+1}-\frac{1}{n}=-\frac{1}{n(n+1)};$$ $$h(n)=2^n\ \Longrightarrow\ (dh)\big( [n,n+1] \big)= 2^{n+1}-2^{n}=2^n.$$
The analogs of the familiar theorems from calculus are trivial.
Theorem (Monotonicity). A $0$-cochain is increasing (decreasing) on an interval if and only if its exterior derivative is positive (negative) on each edge in this interval; i.e., $$\forall A<B,\ f(B)>f(A) \Longleftrightarrow (df) \big(PQ\big) >0\quad \forall A\le P < Q\le B.$$
Corollary (Extreme Values). A $0$-cochain has a local maximum (minimum) at a point if and only if its exterior derivative is positive (negative) to the point's left and negative (positive) to its right; i.e., $$\forall A<C<B,\ f(B)>f(A) \text{ and } f(B)>f(C) \Longleftrightarrow (df) \big(AB\big) >0 \text{ and } (df) \big(BC\big) <0.$$
Theorem (Constant Function). A $0$-cochain is constant on an interval if and only if its exterior derivative on each edge in this interval is zero; i.e., $$f(B)=f(A) \Longleftrightarrow (df) \big(PQ\big) =0\quad \forall A\le P < Q\le B.$$
Corollary. Two $0$-cochains have the same exterior derivative on an interval if and only if their difference is constant on that interval; i.e., $$\forall A<B,\ df =dg \Longleftrightarrow f=g+c \text{ for some } c\in{\bf R}.$$
To summarize, the exterior derivative of a $0$-cochain is the $1$-cochain equal, on each edge, to the difference of its values.
Proposition. The exterior derivative is a linear operator $$d:C^0({\mathbb R})\to C^1({\mathbb R}). $$
Exercise. Prove the proposition.
Algebraic properties of the exterior derivative
We already know that the exterior derivative is linear: $$d(\alpha f+\beta g)=\alpha df+\beta dg,$$ for all cochains $f,g$ and all $\alpha,\beta \in {\bf R}$. Therefore, we have the following two familiar facts:
Theorem (Sum Rule). For any two $k$-cochains $f,g$, we have: $$d(f + g)= df + dg.$$
Theorem (Constant Multiple Rule). For any $k$-cochain $f$ and any $c \in {\bf R}$, we have: $$d(cf) = c\cdot df.$$
Other common formulas look somewhat different.
Theorem (Power Formula). For any positive integer $k$ and any edge $AB$, we have: $$d (A^{\underline {k}})\big(AB\big)=kA^{\underline {k-1}},$$ where $$p^{\underline {q}} := p(p-1)(p-2)(p-3)...(p-q+1). $$
Proof. First, let $A=n,\ B=n+1$. Then $$\begin{array}{lll} d (x^{\underline {k}})\big(AB\big)&=d\big( n(n-1)(n-2)...(n-k+1) \big)\\ &=(n+1)n(n−1)...(n−k+2)−n(n−1)(n−2)...(n−k+2)(n−k+1) \\ &= n(n−1)...(n−k + 2)(n + 1 − (n − k + 1)) \\ &= kn^{\underline {k-1}} . \end{array}$$ $\square$
Theorem (Exponent Formula). For any positive real $b$ and any edge $AB$, we have: $$d(b^A)\big(AB\big)=(b-1)b^A.$$
Exercise. Prove these theorems.
Theorem (Trig Formulas). For any real $t$ and any edge $AB$, we have: $$\begin{array}{lllll} d(\sin tA)\big(AB\big)=2\sin \tfrac{t}{2} \cos t(A+\tfrac{1}{2}),\\ d(\cos tA)\big(AB\big)=-2\sin \tfrac{t}{2} \sin t(A+\tfrac{1}{2}). \end{array}$$
Proof. We use the formulas: $$\begin{array}{lllll} \sin u - \sin v = 2 \sin(\tfrac{1}{2}(u-v)) \cos(\tfrac{1}{2}(u+v));\\ \cos u + \cos v = -2 \sin(\tfrac{1}{2}(u-v)) \sin(\tfrac{1}{2}(u+v)). \end{array}$$ Let $A=n,\ B=n+1$. Then $$d(\sin tA)\big(AB\big)=\sin t(n+1) - \sin tn = 2 \sin(\tfrac{1}{2}t) \cos(\tfrac{1}{2}t(2n+1)).$$ $\square$
Exercise. Finish the proof.
Theorem (Product Rule). Given two $0$-cochains $f,g$, for any edge $AB$, we have: $$d(f \cdot g)\big(AB\big) = f(B)dg\big(AB\big) + df\big(AB \big)g(A).$$
Proof. $$\begin{array}{lll} d(f \cdot g)\big(AB\big)&=(f \cdot g)(B)- (f \cdot g)(A)\\ &=f(B) \cdot g(B)- f(A) \cdot g(A)\\ &=f(B) \cdot g(B)- f(B) \cdot g(A) +f(B) \cdot g(A)- f(A) \cdot g(A)\\ &=f(B) \cdot (g(B)- g(A)) +(f(B) - f(A)) \cdot g(A)\\ &=f(B)dg\big(AB\big) + df\big(AB \big)g(A). \end{array}$$ $\square$
Theorem (Quotient Rule). Given two $0$-cochains $f,g$, any edge $AB$, we have: $$d(f/g)(AB) = \frac{df\big(AB \big)g(A) - f(A)dg\big(AB \big)}{g(A)g(B)},$$ provided $g(A),g(B) \ne 0$.
There are no, in general, compositions of cochains and, therefore, no chain rule.
Exercise. Prove this theorem by following the proof for the Product Rule.
Exercise. Derive the “Power Formula” for $k<0$.
Exercise. Derive the “Log Formula”: $d(\log_b tA) \big(AB \big)=$?
The Fundamental Theorem of Calculus
Given $f \in C^0({\mathbb R})$, let's take our definition of $df \in C^1({\mathbb R})$, $$df\big(AB \big) :=f(B) - f(A),\ AB\in{\mathbb R},$$ and rewrite it in the integral notation: $$\displaystyle\int_{AB} df = f(B) - f(A).$$ Now, what about integration over “longer” intervals? Let $A_0,A_1,...,A_k$ is a sequence of consecutive nodes, $k \in {\bf Z}$. Let's denote this chain by $$A_0A_k := A_0A_1+A_1A_2+...+A_{k-1}A_k.$$ It is a $1$-chain and $df$ is a $1$-cochain. Then we have: $$\begin{array}{llll} df(A_0A_k) &= df\big(A_0A_1&+A_1A_2&+...&+A_{k-1}A_k \big) \\ &= df\big(A_0A_1 \big)&+df\big(A_1A_2 \big)&+...&+df\big(A_{k-1}A_k \big) \\ &= f(A_1)-f(A_0) &+ f(A_2) - f(A_1) &+ ... &+ f(A_k) - f(A_{k-1}) \\ &= f(A_k) -f(A_0) . \end{array}$$ We simply applied the definition repeatedly.
Written in the conventional notation, the result takes this form: $$\displaystyle\int_{A_0A_k} df = f(A_k) -f(A_0).$$
Theorem (Fundamental Theorem of Calculus). Given a $0$-cochain $f$, we have $$\begin{array}{|c|} \hline \\ \quad \displaystyle\int_{AB} df =f(B) -f(A), \quad \\ \\ \hline \end{array}$$ for all nodes A,B, where $AB$ stands for the chain of edges from $A$ to $B$.
This is the theorem's “net change” form.
Let's state the algebraic version of this theorem. First, the right-hand side is re-written: $$\displaystyle\int_{AB} df=df(AB).$$ Now the left-hand side. Observe that $AB$ is a $1$-chain and the nodes $A,B$ make up its boundary: $$\partial \big(AB\big) =B-A,$$ taking into account the direction. Then we can take the above computation one step further: $$\begin{array}{llll} f(B) -f(A)&= f(B -A)\\ &= f\Big(\partial (AB) \Big). \end{array}$$ The resulting interaction of the operators of exterior derivative and boundary is given below.
Theorem (Stokes Theorem). Given a $0$-cochain $f$, we have for any $1$-chain $a$: $$df(a) =f(\partial a),\ \forall a\in C^1({\mathbb R}).$$
In the abbreviated notation it is just another way to state the definition of the exterior derivative: $$\begin{array}{|c|} \hline \\ \quad df =f\partial \quad \\ \\ \hline \end{array}$$
Here is another form of the Fundamental Theorem.
Theorem. Suppose a node $A\in {\mathbb R}$ is fixed. Given a $1$-cochain $g$, define a $0$-cochain by $$f(B):=\int_{AB} g,\ \forall B\in {\mathbb R},$$ where $AB$ stands for the chain of edges from $A$ to $B$. Then $$df=g.$$
In other words, $g$ is an antiderivative of $f$.
Exercise. Prove the theorem. Hint: why is it well-defined?
The geometry of ${\mathbb R}$
So far, we have been able to develop a fair portion of calculus under the assumption that the nodes are placed at the integer locations: $$..-1,0,1,2,3,4....$$ Of course, there is nothing special about this arrangement and, in general, we should allow arbitrary locations for the nodes: $$...<A<B<C<D<...$$
Here, $...,A,B,C,...$ are simply the names of the nodes. The specific path we take is however different: we endow ${\mathbb R}$ with a geometric structure.
First, we assign lengths to each of the edges, as follows. If $A,A'$ are two consecutive nodes, we have a corresponding positive real number for the length $|AA'|$ of this edges: $$AA'\mapsto |AA'|\in {\bf R}_+.$$
For example, for all the previous developments we could have assumed that $|AA'|=1$.
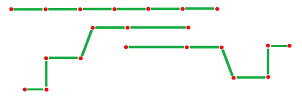
Even though it seems that we have accomplished our goal, we notice that even when these numbers are specified, the geometry of ${\mathbb R}$ remains underdetermined. To clarify this idea, let's think of the nodes as hinges that connect rods of specific lengths. Then, the construction isn't rigid:
Now let's imagine connecting the centers of the rods with a new set of rods:
In other words, there is a new edge for each node of ${\mathbb R}$ and its length is specified:
There are also a new node for each edge in ${\mathbb R}$. Together, these new nodes and edges form a new copy of ${\mathbb R}$ with (possibly different) lengths. It is denoted by ${\mathbb R}^\star$.
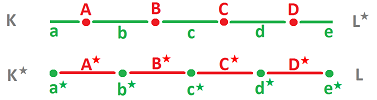
This is how the cells of the two are matched:
- an edge $a$ in ${\mathbb R}$ corresponds to a node $a^\star$ in ${\mathbb R}^\star$; and
- a node $A$ in ${\mathbb R}$ corresponds to an edge $A^\star$ in ${\mathbb R}^\star$. $\\$
We have a one-to-one correspondence between the original, called primal, cells and the new, called dual, cells: $$\begin{array}{llll} 1\text{-cell (primal)} &\longleftrightarrow &0\text{-cell (dual)} \\ 0\text{-cell (primal)} &\longleftrightarrow &1\text{-cell (dual)} \end{array}$$ The combined correspondence is stated for $k=0,1$:
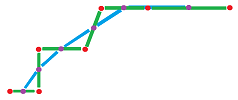
Indeed, the correspondence can be reversed! Below, is $K={\mathbb R}$ or $L={\mathbb R}$?
The new domain ${\mathbb R}^\star$ is a full copy of the old domain ${\mathbb R}$.
Indeed, ${\mathbb R}^\star$ has a collection of nodes and a collection of edges with the same boundary relation between them: $$\partial AB=B-A,$$ for any consecutive nodes $A,B$ in ${\mathbb R}^\star$. The chains are also defined, $C_k({\mathbb R}^\star),k=0,1$, as linear combinations of $k$-cells. The boundary operator is defined between them: $$\partial:C_1({\mathbb R}^\star)\to C_0({\mathbb R}^\star).$$ The new domain also has the full set of $k$-cochains as real-valued functions on its $k$-cells. They are called dual cochains while the ones on ${\mathbb R}$ are called primal cochains. The exterior derivative is also given: $$d:C^0({\mathbb R}^\star)\to C^1({\mathbb R}^\star).$$
There is a direct relation between these two calculi.
Proposition. Given a primary $k$-cochain $s$, $k=0,1$, the following is a dual $(1-k)$-cochain: $$s^\star (a):=s(a^\star),\ \forall a\in C_k({\mathbb R}^\star).$$
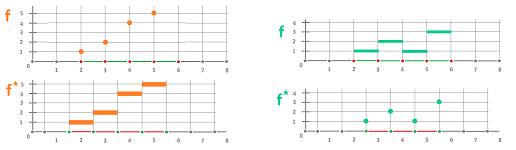
For the standard geometry, the duality of cochains is illustrated below:
The derivative as the rate of change
The presence of the geometry of ${\mathbb R}$ allows us to define the first derivative of a discrete function (i.e., a $0$-cochain) as “the rate of change” instead of just “change”, which is the exterior derivative.
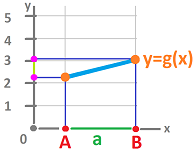
Recall that, for a real-valued function $y=g(x)$, the rate of change is $$\frac{\text{change of } y}{ \text{change of } x}=\frac{g(B)-g(A)}{B-A},$$ over some interval $[A,B]$ in its domain. It is important to realize here that the definition remains equivalent when the denominator is required to be positive, i.e., $A<B$.
Now, this is the setting of ${\mathbb R}$:
We would like to know the rate of change of a $0$-cochain over an interval. In fact, we only care about the case when this interval is simply an edge in ${\mathbb R}$. Then the meaning of the fraction above (with a positive denominator) is $$\frac{g(B)-g(A)}{|AB|}.$$ The numerator is easily recognized as $dg(a)$, the exterior derivative $dg$ of the $0$-cochain $g$ evaluated at the edge $a=AB$.
The only question remains, where this new number should be assigned? If it was assigned to the edge $a$, we would have simply a multiple of the exterior derivative. This makes it a $1$-cochain! The fact that there is no derivative of a $1$-chain precludes the possibility of the second exterior derivative to have any meaning. Instead, we utilize the dual structure of ${\mathbb R}^\star$ and assign the value of the above ratio to the node dual to $a$, as follows.
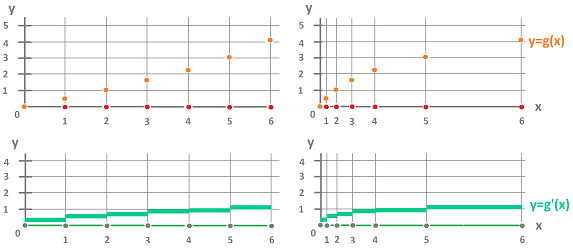
Definition. The derivative of a primal $0$-cochain $g$ is the dual $0$-cochain given by its values at the nodes of ${\mathbb R}^\star$: $$g'(P):=\frac{dg(P^\star)}{|P^\star|},\ \forall P\in {\mathbb R}^\star.$$
It can be further differentiated, as discussed in the next subsection.
Proposition. The derivative is the dual of the exterior derivative: $$g'=(dg)^\star.$$
This is how the definition works in the case of edges with equal lengths:
The formula is simple. Then, the Sum Rule, the Constant Multiple Rule, the Product Rule, and the Quotient Rule all hold. Furthermore, the denominator is the only thing we need to add to state the algebraic properties of the derivative.
We can be more specific in the flat case: $$\big |[n,n+1] \big|= \big |[n-\tfrac{1}{2},n+\tfrac{1}{2}] \big| = h.$$ Then, we have the following:
- Power Formula:
$$(n^{\underline {k}})'\big(n+\tfrac{1}{2}\big)=\frac{k}{h}n^{\underline {k-1}}.$$
- Exponent Formula:
$$(b^n)'\big(n+\tfrac{1}{2}\big)=\frac{k}{h}(b-1)b^n.$$
- Trig Formulas:
$$\begin{array}{lllll} (\sin tn)'\big(n+\tfrac{1}{2}\big)=\frac{2}{h}\sin \tfrac{t}{2} \cos t(n+\tfrac{1}{2}),\\ (\cos tn)'\big(n+\tfrac{1}{2}\big)=-\frac{2}{h}\sin \tfrac{t}{2} \sin t(n+\tfrac{1}{2}). \end{array}$$
Exercise. Derive the “Power Formula” for $k<0$ and the “Log Formula” for the derivative.
Further, for $0$-cochains $f$ and $g$, we have $$f'=g' \Longleftrightarrow df=dg.$$ Secondly, the sign of the exterior derivative and that of the derivative coincide. These two facts allow us to restate the simple calculus theorems about the exterior derivative.
Theorem (Monotonicity). A $0$-cochain is increasing (decreasing) on an interval if and only if its derivative is positive (negative) on each edge in this interval; i.e., $$\forall A<B,\quad f(B)>f(A) \Longleftrightarrow f' \big(PQ^\star\big) >0\quad \forall A\le P < Q\le B.$$
Corollary (Extreme Values). A $0$-cochain has a local maximum (minimum) at a point if and only if its derivative is positive (negative) to point's left and negative (positive) to its right; i.e., $$\forall A<C<B,\quad f(B)>f(A) \text{ and } f(B)>f(C) \Longleftrightarrow f' \big(AB^\star\big) >0 \text{ and } f' \big(BC^\star\big) <0.$$
Theorem (Constant Function). A $0$-cochain is constant on an interval if and only if its derivative on each edge in this interval is zero; i.e., $$f(B)=f(A) \Longleftrightarrow f' \big(PQ^\star\big) =0\quad \forall A\le P < Q\le B.$$
Corollary. Two $0$-cochains have the same derivative if and only if their difference is constant on that interval; i.e., $$\forall A<B,\quad f'=g' \Longleftrightarrow f=g+c \text{ for some } c\in{\bf R}.$$
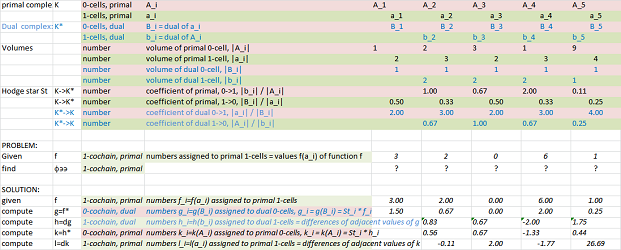
The derivative is computed with a spreadsheet:
Link to file: Spreadsheets.
The second derivative of a $0$-cochain
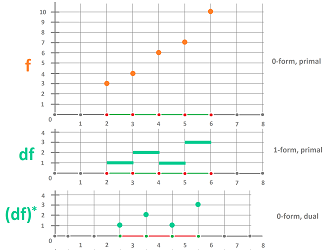
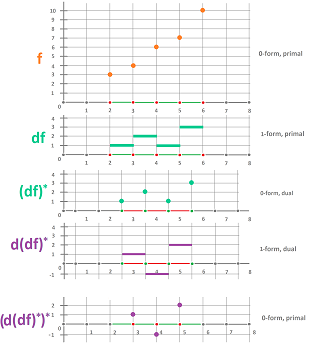
We will now consider the role of geometry in the issue of concavity. This is what we observe: shrinking, stretching, or deforming the $x$- or the $y$-axes won't change the monotonicity of a function but it will change its concavity. Below, we have deformed the $x$-axis and changed the concavity of the graph at $x=1$:
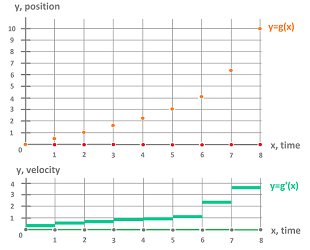
The sign of the exterior derivative will tell us the difference between increasing and decreasing behavior. We need a similar tool to evaluate the concavity which is a concept that captures the shape of the graph of a function in calculus as well as the acceleration in physics. For example, the upward concavity of the discrete function below is obvious, which indicates a positive acceleration:
We start over and look at the change of change. This quantity can be seen algebraically as the increase of the exterior derivative (i.e., the change): $$g(2)-g(1) < g(3)-g(2),\quad g(3)-g(2) < g(4)-g(3),\quad \text{ etc.}$$ But do these inequalities imply concavity? Not without assuming that the intervals have equal lengths!
Below, we have two identical discrete function with, of course, identical exterior derivatives:
...but with the opposite concavities!
For a real-valued function $g$, the change of change at point $B$ is known to be $$\frac{\frac{g(C)-g(B)}{B-C} - \frac{g(B)-g(A)}{A-B}}{(A-C)/2}.$$ for some $A,C$ with $B$ between them. This is the setting of discrete calculus:
We are to find the rate of change of the first derivative -- from one edge to the adjacent one. It is important to notice here that the definition remains equivalent when the denominators are required to be positive, i.e., $A<C$. We can re-write then: $$\frac{\frac{g(C)-g(B)}{|BC|} - \frac{g(B)-g(A)}{|AB|}}{|AC|/2}.$$
Let's take a closer look at this formula.
The numerators of the two fractions are easily recognized as the exterior derivative of the $0$-cochain $g$ evaluated at the $1$-cells $a$ and $b$ respectively. Meanwhile, the denominators are the lengths of these cells.
The denominator is, in fact, the distance between the centers of the cells $a$ and $b$. Therefore, we can think of it as the length of the dual cell of the vertex $B$. Then, we define the second derivative (not to be confused with $ddg$) of a $0$-cochain $g$ as follows.
Definition. The second derivative of a primal $0$-cochain $g$ is a primal $0$-cochain given by its values at the nodes of ${\mathbb R}^\star$: $$g' '(B)=\frac{\frac{dg(b)}{|b|} - \frac{dg(a)}{|a|}}{|B^\star|},\ \forall B\in {\mathbb R}^\star,$$ where $a,b$ are the $1$-cells adjacent to $B$.
We take this one step further. What is the meaning of the difference in the numerator? Combined with the denominator, it is the derivative of $g'$ as a dual $0$-cochain. The second derivative is indeed the derivative of the derivative: $$g' '=(g')'.$$ The formula is illustrated by the following duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &g' '\ ..\ g\ & \ra{d}& dg &\\ &\ua{\star} & \ne & \da{\star} & \\ &d(g')& \la{d} & g'& \\ \end{array} $$
This is how the formula works in the case of edges with equal lengths:
The second derivative is computed with a spreadsheet:
Computing the second derivative with a non-trivial geometry is slightly more complex:
Link to file: Spreadsheets.
In the pursuit of closed solutions, we will use this notation for the primal and dual edges: $$I_n:=[n,n+1] , \quad I_n^\star:= [n-\tfrac{1}{2},n+\tfrac{1}{2}],$$ and for their lengths: $$\Delta _n:=| I_n |, \quad \Delta _n^\star:=| I_n^\star |.$$ Then, $$f'(n+\tfrac{1}{2})=\frac{f(n+1)-f(n)}{\Delta_n},$$ $$f' '(n)=\frac{\frac{f(n+1)-f(n)}{\Delta_n} - \frac{f(n)-f(n-1)}{\Delta_{n-1}}}{\Delta_n^\star /2}.$$
In the case of the uniform geometry of ${\mathbb R}$, i.e., $\Delta_n=\Delta_n^\star:=h$, the formulas are simplified: $$f'(n+\tfrac{1}{2})=\frac{f(n+1)-f(n)}{h},$$ $$f' '(n)=\frac{f(n+1)-2f(n)+f(n-1)}{h^2 /2}.$$ Or, $$f' '(n)=\frac{f'(n+\tfrac{1}{2})-f'(n-\tfrac{1}{2})}{h /2}.$$
Example. Let's compute the second derivative of $f(n)=\sin tn$. We have $$\begin{array}{lllll} f' '(n)&=\frac{2}{h}\Big( \frac{2}{h}\sin \tfrac{t}{2} \cos t(n+\tfrac{1}{2}) - \frac{2}{h}\sin \tfrac{t}{2} \cos t(n-\tfrac{1}{2}) \Big) ,\\ &=\frac{2}{h^2}\sin \tfrac{t}{2} \Big( \cos t(n+\tfrac{1}{2}) - \cos t(n-\tfrac{1}{2}) \Big) ,\\ &=-\frac{4}{h^2}\sin \tfrac{t}{2} \sin(\tfrac{1}{2}t) \sin(\tfrac{1}{2}t(2n))\\ &=-\frac{4}{h^2}\sin^2 \tfrac{t}{2} \sin tn, \end{array}$$ by the formula $$\cos u − \cos v = −2 \sin(\tfrac{1}{2}(u-v)) \sin(\tfrac{1}{2}(u+v)).$$ Then we have an ODE: $$f' '=-k f, \text{ where } k=\frac{4\sin^2\tfrac{t}{2}}{h^2}>0.$$ $\square$
Exercise. Compute the second derivatives of $n^2,\ b^n,\ \cos n$, etc.
Without this restriction, closed formulas for derivatives are hard to come by even in the simplest cases.
Example. Let's compute the second derivative of $f(n)=cn,\ c\in {\bf R}$. We have: $$\begin{array}{lll} f' '(n)&=\frac{\frac{c(n+1)-cn}{\Delta_n} - \frac{cn-c(n-1)}{\Delta_{n-1}}}{\Delta_n^\star /2}\\ &=c\frac{\frac{1}{\Delta_n} - \frac{1}{\Delta_{n-1}}}{\Delta_n^\star /2}= &=c\frac{\Delta_{n-1}-\Delta_n}{\Delta_{n-1}\Delta_{n}\Delta_n^\star /2}.\\ \end{array}$$ $\square$
Newtonian physics, the discrete version
The concepts introduced above allow us to state some elementary facts about the discrete Newtonian physics, in dimension $1$.
First, the time is given by the standard metric complex $K:={\mathbb R}$, at the simplest. Note that, even though it is natural to assume that the complex that represents time has no curvature, it is still might be important to be able to handle time intervals of various lengths.
Second, the space is given by any ring $R$, in general. For all the derivatives to make sense at once, we can choose the standard geometry for the time domain ${\mathbb R}$. Note that there is no topology and, consequently, there can be no assumptions about continuity.
The main quantities we are to study are:
- the location $r$ is a primal $0$-cochain;
- the displacement $dr$ is a primal $1$-cochain;
- the velocity $v=r'$ is a dual $0$-cochain;
- the momentum $p=mv$, where $m$ is a constant mass, is also a dual $0$-cochain;
- the impulse $J=dp$ is a dual $1$-cochain;
- the acceleration $a=r' '$ is a primal $0$-cochain.
Some of these cochains are seen in the following duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{lllll} &a\ ..\ r\ & \ra{d}& dr &\\ &\ua{\star} & \ne & \da{\star} & \\ &J/m& \la{d} & v& \\ \end{array} $$
Newton's First Law: If the net force is zero, then the velocity $v$ of the object is constant: $$F=0 \Longrightarrow v=const.$$
The law can be restated without invoking the geometry of time:
- If the net force is zero, then the displacement $dr$ of the object is constant:
$$F=0 \Longrightarrow dr=const.$$ The law shows that the only possible type of motion in this force-less and distance-less space-time is uniform; i.e., it is a repeated addition: $$r(t+1)=r(t)+c.$$
Newton's Second Law: The net force on an object is equal to the derivative of its momentum $p$: $$F=p'.$$
As we have seen, the second derivative is meaningless without specifying geometry, the geometry of time.
Newton's Third Law: If one object exerts a force $F_1$ on another object, the latter simultaneously exerts a force $F_2$ on the former, and the two forces are exactly opposite: $$F_1 = -F_2.$$
Law of Conservation of Momentum: In a system of objects that is “closed”; i.e.,
- there is no exchange of matter with its surroundings, and
- there are no external forces; $\\$
the total momentum is constant: $$p=const.$$
In other words, $$J=dp=0.$$ To prove, consider two particles interacting with each other. By the third law, the forces between them are exactly opposite: $$F_1=-F_2.$$ Due to the second law, we conclude that $$p_1'=-p_2',$$ or $$(p_1+p_2)'=0.$$
Exercise. State the equation of motion for a variable-mass system (such as a rocket). Hint: apply the second law to the entire, constant-mass system.
Exercise. Create a spreadsheet for all of these quantities.
To study physics in dimension $3$, one simply combines three cochains for each of the above quantities: $$f_i:{\mathbb R}\to {\bf R},\ i=1,2,3,$$ into one: $$f=(f_1,f_2,f_3):{\mathbb R}\to {\bf R}^3.$$