Spreadsheets

Topology

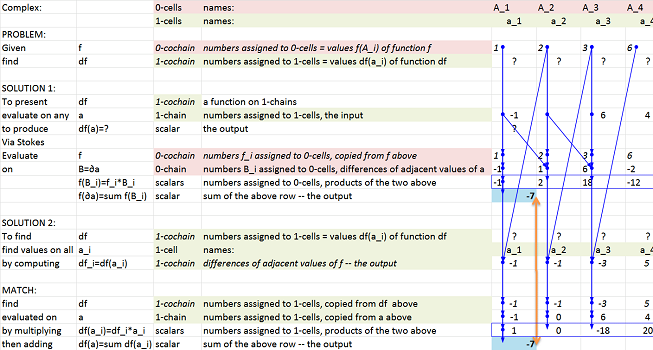
Boundary operator: boundary_operator_binary.xlsx

boundary_dim_1.xlsx

Link to the file: boundary_dim_2.xlsx

Vector fields

Settings

For motion simulation, do one step at a time:

Flow simulation

Dimension 1

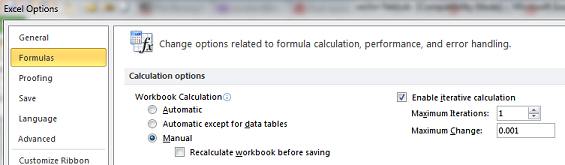
The settings for formulas are:

• Manual,
• 1 Iteration.
• Push: Calculate now

Link to the file: vector field_dim_1.xlsx

Dimension 2

Same settings.

Link to the file: vector field_dim_2.xlsx Link to the file: vector field_dim_2.xlsx

Differential forms

Settings

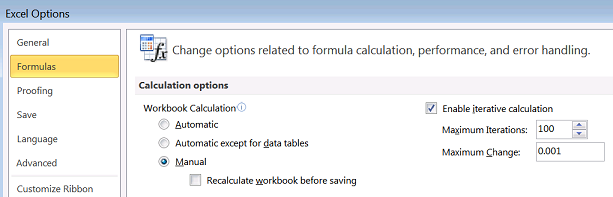
For some simulations iterations are required:

Dimension 1

Boundary operator:

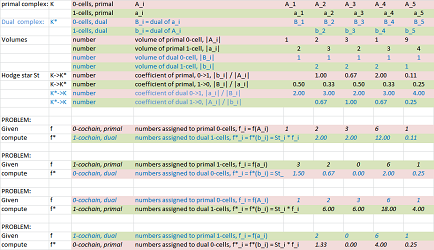
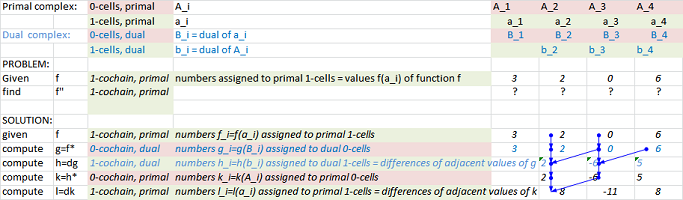
Link to the file: boundary_dim_1.xlsx

Exterior derivative:

Link to the file: Exterior_derivative_dim_1.xlsx

Hodge duality:

Link to the file: Hodge_duality_dim_1.xlsx

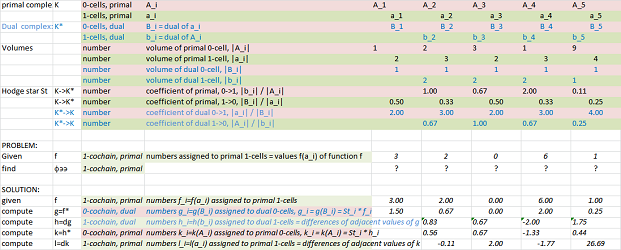
Hodge duality with geometry:

Link to the file: Hodge_duality_dim_1_w_geometry.xlsx

Laplacian:

Link to the file: Laplacian_dim_1.xlsx

Laplacian with geometry:

Link to the file: Laplacian_dim_1_w_geometry.xlsx

Dimension 2

Warning: you will need to use a buffer sheet because Excel's row-by-row manner of evaluation will cause a skewed pattern:

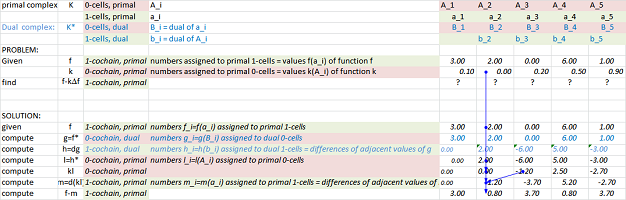
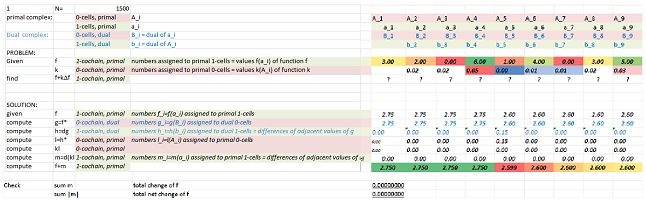
Diffusion

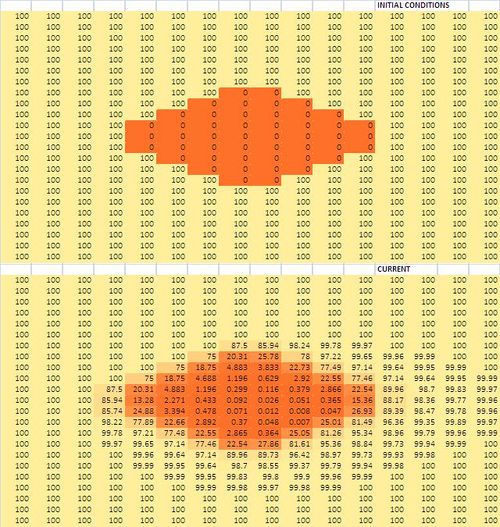
The recursive formula for the simulation: $$U(a, t+1):= U(a,t) + \Big[- k(a) \left( U(a) - U(a-1)\right) + k(a+1) \left( U(a+1) - U(a)\right)\Big].$$ The Excel setup is shown below:

The result after $1,500$ iterations is shown next:

Files:

• diffusion_dim_1.xlsx
• diffusion_dim_1_iterated.xlsx

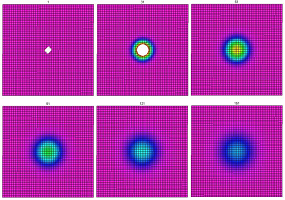
Dimension $2$.

A simulation of heat transfer from single point is shown below:

File:

• diffusion.xlsx

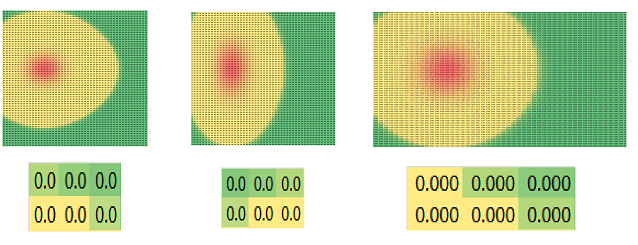
What if the horizontal walls are longer than the vertical ones? Then more heat should be exchanged across the vertical walls than the horizontal ones: $$RC= RC - k*\bigg( .5*\left(RC-RC[-1]\right) + .5*\left(RC-RC[1]\right) + 2*\left(RC-R[-1]C\right) + 2*\left(RC-R[1]C\right) \bigg).$$ As a result, the material does travel farther -- as measured by the number of cells -- in the vertical direction (second image) than normal (first image):

Wave propagation

Dimension $1$:

The Excel formula is:

• =R1C5*R[-1]C[-1]+2*(1-R1C5)*R[-1]C+R1C5*R[-1]C[1]-R[-2]C

Here cell R1C5 contains the value of $\alpha$.

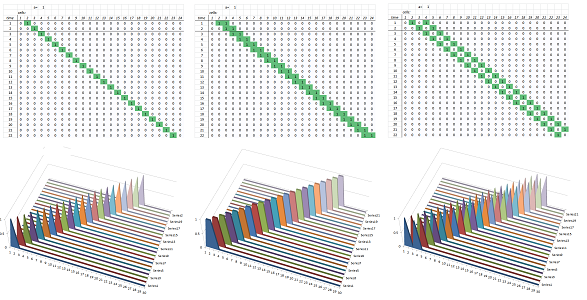
The simplest propagation pattern is given by $\alpha=1$. Below we show the propagation of a single bump, a two-cell bump, and two bumps:

Dimension $2$:

Social choice

To experiment with PageRank, use Link to the file: Spreadsheets.this spreadsheet: pagerank.xlsx.

To experiment with decycling comparison elections, use this spreadsheet: decycled_elections.xlsx.