Graph representation of gray scale images

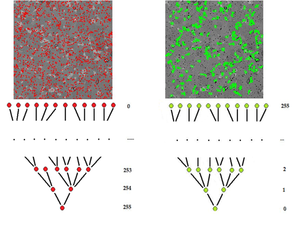
More precisely, this article is about graph representation of the topology of gray scale images (an image becomes a graph when one uses adjacency). The connected components of upper and lower level sets of the gray scale function are building blocks of segmentation.

The idea is that it is unlikely that a boundary of a real object depicted in the image cutting through upper or lower level sets. However, one can imagine a picture with bald spot merging with the sky behind.

Inclusion tree

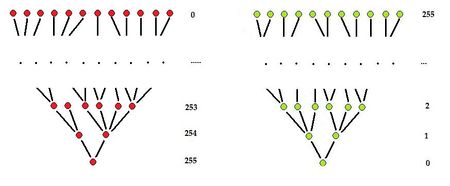
The connected components of the lower level sets have a clear hierarchy based on inclusion. This hierarchy provides a graph representation of the topology of the image.

First the original image – just a blurred black circle.

Second, its level curves, with the lower level sets inside.

Third, they are ordered by inclusion and this fact is reflected in the structure of the tree.

Such an arrangement of sets is represented by an inclusion tree. In general the inclusion tree of an image may be complex.

Possible inclusion trees for the lower (left) and upper (right) level sets.

Similar analysis applies to upper level sets – light holes in dark components. See also Tree representation of images.

An example of an lower level set.

An example of an lower level set.

The problem with inclusion trees: The inclusion trees for upper and lower level sets, if considered separately, do not help in finding out which object has which hole. Therefore, in order to capture the topology of the image (with holes), the two trees have to be combined in some way.

Combined inclusion tree

An image of a blurred ring.

Blurred ring with contours.

The combined inclusion tree for the blurred ring.

Level set are the boundaries of the upper and lower level sets. The Jordan Theorem implies that a component of a level set encircles or is encircled by components of other level sets. Then the outer borders of the lower and upper level sets are still ordered and the result is a tree.

For example: P. Monasse and F. Guichard, Fast computation of a contrast invariant image representation. IEEE Transactions on Image Processing, 9(5), pp. 860–872, 2000.

How the combined inclusion tree is built from the two inclusion trees.

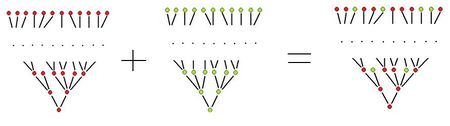
This is how the lower and upper level trees are normally merged. There are drawbacks for this approach.

• The lower level sets are mixed with the upper level sets.
• The gray levels are also mixed.

The topology graph of the image

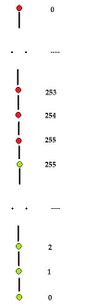
There is an alternative way to combine the inclusion trees.

How the topology graph is built from the two inclusion trees: turn the latter upside down and attach along the levels.

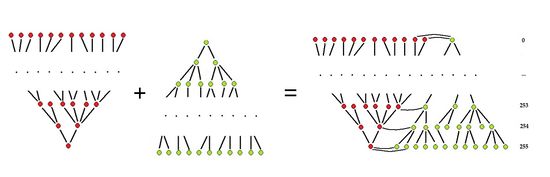
The upper level tree is turned upside down and attached to the lower level tree – along the aligned layers corresponding to the gray levels. (Reminds slightly of the structure of the DNA.)

Differences:

• The lower and upper inclusion trees remain intact within the graph.
• The graph breaks into layers that coincide with the topology graphs of the binary images obtained via thresholding.
• The topology graph is not a tree in general.

For more details see Topology graph.

See also Graph representation of color images.