This site is being phased out.
Tree representation of images
More precisely, it's about tree representation of the topology of images...
We address here the issue of image segmentation of binary and gray scale images. The scientific foundation of the proposed method is topology, the science of continuity and connectedness.
Contents
Introduction
The topological analysis is intended to reveal the most basic things about the image: how many connected components are present, which ones have holes and how many, i.e., counting. It is also a part of the analysis to capture these topological features. The next stage is geometric: measuring them and finding their locations. With this data, it may be possible to understand the content of the image.
We use the tools that are standard in the discipline. The first tool is cell decomposition of images: the image is represented as a combination of pixels as well as their edges and vertices. The second tool is cycles: both the connected components and the holes are captured by circular sequences of edges.
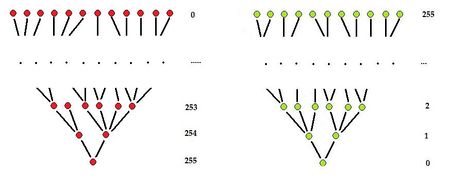
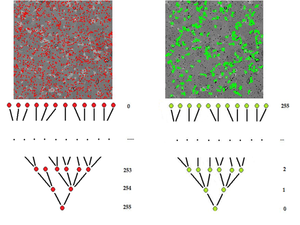
The challenge is that these topological tools have not been commonly applied in the analysis of gray scale images. For example, while in binary images the meaning of connected components is clear, for gray scale images, a “connected component” should be a dark region surrounded by a lighter area. In other words, it is a lower level set of the gray scale function. To deal with the multitude of lower level sets we record them in a tree. This graph captures the inclusion hierarchy among the lower level sets. It may be called the inclusion tree. A similar data structure is created for the holes (with the upper level sets). Combined these two graphs represent the topology of the image, the topology graph. It is the foundation of the image analysis algorithm of Pixcavator.
The connected components of upper and lower level sets of the gray scale function are building blocks of segmentation.
The idea is that it is unlikely that a boundary of a real object depicted in the image cutting through upper or lower level sets. However, one can imagine a picture with bald spot merging with the sky behind.
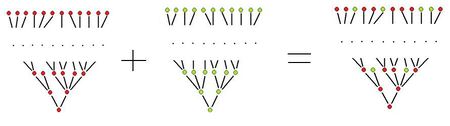
Inclusion tree
The connected components of the lower level sets have a clear hierarchy based on inclusion. This hierarchy provides a graph representation of the topology of the image.
Such an arrangement of sets is represented by an inclusion tree. In general the inclusion tree of an image may be complex.
Similar analysis applies to upper level sets – light holes in dark components. See also Tree representation of images.
The problem with inclusion trees: The inclusion trees for upper and lower level sets, if considered separately, do not help in finding out which object has which hole. Therefore, in order to capture the topology of the image (with holes), the two trees have to be combined in some way.
Combined inclusion tree
Level set are the boundaries of the upper and lower level sets. The Jordan Theorem implies that a component of a level set encircles or is encircled by components of other level sets. Then the outer borders of the lower and upper level sets are still ordered and the result is a tree.
For example: P. Monasse and F. Guichard, Fast computation of a contrast invariant image representation. IEEE Transactions on Image Processing, 9(5), pp. 860–872, 2000.
This is how the lower and upper level trees are normally merged. There are drawbacks for this approach.
- The lower level sets are mixed with the upper level sets.
- The gray levels are also mixed.
The topology graph of the image
There is an alternative way to combine the inclusion trees.
The upper level tree is turned upside down and attached to the lower level tree – along the aligned layers corresponding to the gray levels. (Reminds slightly of the structure of the DNA.)
Differences:
- The lower and upper inclusion trees remain intact within the graph.
- The graph breaks into layers that coincide with the topology graphs of the binary images obtained via thresholding.
- The topology graph is not a tree in general.
For more details see Topology graph. See also Graph representation of color images.
Other methods
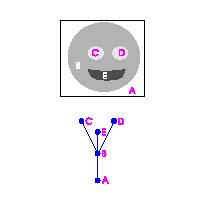
There are a few papers on this subject. One of them has an especially simple example:
J. Andrew Bangham, J. R. Hidalgo, Richard Harvey, Gavin C. Cawley, The Segmentation of Images via Scale-Space Trees, British Machine Vision Conference, 1998.
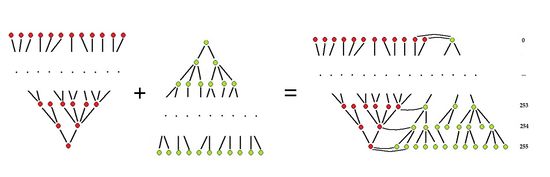
Their algorithm (called "sieve") produces a tree decomposition of gray scale images as follows. It cuts (simultaneously!) minima and maxima of the gray scale function - slice by slice. The result is a hierarchy of objects (called "granulas") that is recorded as a tree. Their example is below.
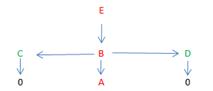
This tree may resemble the topology graph – until you build one. This is what it looks like. Here the gray scale levels run from 0 (E) to 255 (A).
Generally, the topology graph isn't a tree (try the negative of this image). This comes as a consequence of treating light and dark objects (maxima and minima) separately and independently. Indeed, dark objects may merge or light objects may split etc as you go up the gray levels.
There are other issues. First, the central (in my view) question of what is object in a gray scale image and how to count them isn’t addressed in this and related papers. Second, the approach is only partially applicable to 3D images as there is no way of capturing tunnels without homology. Third, it is unclear how this approach can be applied to color images. As for Image simplification, since it is carried out via the sieve, the granule removal is based on size only.
In spite of the differences the testing presented in this paper validates our approach.