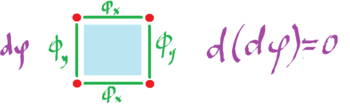Calculus on chains

Bird's-eye view of calculus

With the help of duality we have a bird's-eye view of (a large part of) calculus, as follows.

Suppose we are given a cubical complex and on this complex we have the vector spaces of $k$-chains $C_k$. Combined with the boundary operator $\partial$ they form the chain complex $\{C_*,\partial\}$ of $K$: $$\ldots\stackrel{\partial}{\rightarrow}C_{n+1}\stackrel{\partial}{\rightarrow}C_{n}\stackrel{\partial}{\rightarrow}\ldots \stackrel{\partial}{\rightarrow}C_{0}\stackrel{\partial}{\rightarrow}0.$$

If we "dualize" this diagram, we have another sequence of vector spaces and linear operators: $$\ldots\stackrel{\partial^*}{\leftarrow}(C_{n+1})^*\stackrel{\partial^*}{\leftarrow}(C_{n})^*\stackrel{\partial^*}{\leftarrow}\ldots \stackrel{\partial^*}{\leftarrow}(C_{0})^*\stackrel{\partial^*}{\leftarrow}0.$$ The dimension of each of these spaces matches that of the space above while the matrices of the operators are the transposes of the ones above.

But this is simply the cochain complex $\{C^*,d\}$: $$\ldots\stackrel{d}{\leftarrow}C^{n+1}\stackrel{d}{\leftarrow}C^{n}\stackrel{d}{\leftarrow}\ldots \stackrel{d}{\leftarrow}C^{0}\stackrel{d}{\leftarrow}0,$$ where $d$ is the discrete exterior derivative. The conclusion is based on the shortest version of the Stokes Theorem: $$\partial ^*=d.$$

Main properties of exterior derivative

The theorems below are counterparts of the ones about continuous forms.

Theorem. $d \colon C^k(R) \rightarrow C^{k+1}(R)$ is linear.

To prove we just look where the basis elements goes under $d$. The "standard" basis of $C^k(R)$ consists of forms $\alpha _a$ with a single non-zero entry -- for a single $k$-cell $a$. Finish this argument (Exercise).

Theorem (Product Rule - Leibniz Rule) $d(\varphi \wedge \psi) = d \varphi \wedge \psi + (-1)^k \varphi \wedge d \psi$.

Exercise: Prove for dimension 2.

Theorem (Topological Property). $dd \colon C^k(R) \rightarrow C^{k+2}(R)$ is zero.

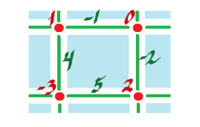
For $R = {\bf R}^2$, $k=0$, proof is easy, as follows.

• $0$-form $f$ given:

• Compute $1$-form $df$ (green);
• Compute $2$-form $ddf$, as follows:

$\begin{align*} d(df) &= (B_x - A_y) dx \hspace{1pt} dy \\ &= ((-2 -4) - (-1 -5))dx \hspace{1pt} dy \\ &= 0. \end{align*}$

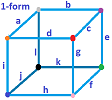
Exercise: Prove $dd \colon C^1({\bf R}^3) \rightarrow C^3({\bf R}^3)$ is zero.

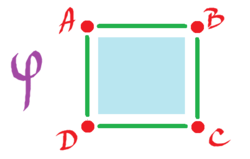
Proof for $dd=0 \colon C^0({\bf R}^2) \rightarrow C^2({\bf R}^2)$.

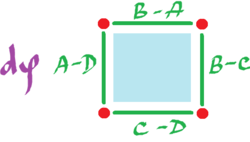
Here $A,B,C,D$ are the values of $0$-form $\varphi$ at these vertices. Let $d\varphi = \Phi$.

These are the values of this $1$-form at these edges:

Compute: $$-(B-A) + (C-D) + (B-C) - (A-D) = 0,$$ where the first two are vertical and the second two are horizontal. This means the two mixed partial derivatives are equal: $$\Phi_{xy} = \Phi_{yx}$$ just as in Clairaut's theorem. $\blacksquare$

So, instead of using $dx \hspace{1pt} dy, dy \hspace{1pt} dz$, etc (differential forms) to prove that $dd=0$ for ${\bf R}^3$, one can draw a diagram like the one above and use cochains.

Exercise: 1. Given

Compute $dd \colon C^1 \rightarrow C^3$.

2. $dd=0$ for cochains.

The general case follows from the fact that the exterior derivative of cubical forms is dual of the boundary operator of cubical complex. Indeed $$dd=\partial ^* \partial ^* = (\partial \partial)^* = 0^*=0.$$