This site is being phased out.
Dual space
Vectors and covectors
What is the relation between $2$, the counting number, and "doubling", the function $f(x)=2\cdot x$?
Linear algebra helps one appreciate this seemingly trivial relation. Indeed, the answer is a linear operator $$D : {\bf R} \rightarrow L({\bf R},{\bf R}),$$ from the reals to the vector space of all linear functions. In fact, it's an isomorphism!
More generally, suppose $V$ is a vector space. Let $$V^* = \{ \alpha \colon V \rightarrow {\bf R}, \alpha {\rm \hspace{3pt} linear}\}.$$ It's the set of all linear "functionals", also called covectors, on $V$. It is called the dual of $V$.
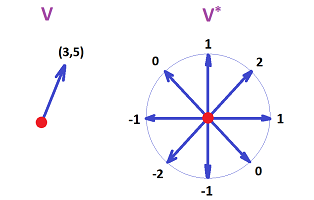
An illustration of a vector in $V={\bf R}^2$ and a covector in $V^*$.
Here a vector is just a pair of numbers, while a covector is a correspondence of each unit vector with a number. The linearity is visible.
Note. If $V$ is a module over a ring $R$, the dual space is still the set of all linear functionals on $V$: $$V^* = \{ \alpha \colon V \rightarrow R, \alpha {\rm \hspace{3pt} linear}\}.$$ The results below apply equally to finitely generated free modules.
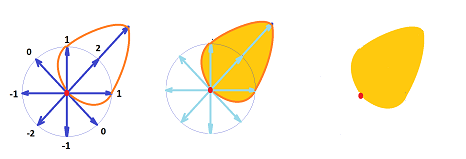
In the above example, it is easy to see a way of building a vector from this covector. Indeed, let's pick the vector $v$ such that
- the direction of $v$ is that of the one that gives the largest value of the covector $w$ (i.e., $2$), and
- the magnitude of $v$ is that value of $w$.
So the result is $v=(2,2)$. Moreover, covector $w$ can be reconstructed from this vector $v$. (Cf. gradient and norm of a linear operator.)
This is how the covector above can be visualized:
It is similar to an oil spill.
Properties
Fact 1: $V^*$ is a vector space.
Just as any set of linear operators between two given vector spaces, in this case $V$ and ${\bf R}$. We define the operations for $\alpha, \beta \in V^*, r \in {\bf R}$: $$(\alpha + \beta)(v) = \alpha(v) + \beta(v), v \in V,$$ $$(r \alpha)(w) = r\alpha(w), w \in V.$$
Exercise. Prove it. Start with indicating what $0, -\alpha \in V^*$ are. Refer to theorems of linear algebra, such as the "Subspace Theorem".
Below we assume that $V$ is finite dimensional.
Fact 2: Every basis of $V$ corresponds to a dual basis of $V^*$, of the same size, built as follows.
Given $\{u_1,\ldots,u_n\}$, a basis of $V$. Define a set $\{u_1^*,\ldots,u_n^*\} \subset V^*$ by setting: $$u_i^*(u_j)=\delta _{ij} ,$$ or $$u_i^*(r_1u_1+\ldots+r_nu_n) = r_i, i = 1,\ldots,k.$$
Exercise. Prove that $u_i^* \in V^*$.
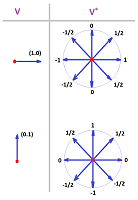
Example. Dual bases for $V={\bf R}^2$:
Theorem. The set $\{u_1^*,\ldots,u_n^*\}$ is linearly independent.
Proof. Suppose $$s_1u_1^* + \ldots + s_nu_n^* = 0$$ for some $r_1,\ldots,r_k \in {\bf R}$. This means that $$s_1u_1^*(u)+\ldots+s_nu_n^*(u)=0 \hspace{7pt} (1)$$ for all $u \in V$.
We choose $u=u_i, i=1,\ldots,n$ here and use $u_j^*(u_i)=\delta_{ij}$. Then we can rewrite (1) with $u=u_i$ for each $i=1,\ldots,n$ as: $$s_i=0.$$ Therefore $\{u_1^*,\ldots,u_n^*\}$ is linearly independent. $\blacksquare$
Theorem. $\{u_1^*,\ldots,u_n^*\}$ spans $V^*$.
Proof. Given $u^* \in V^*$, let $r_i = u^*(u_i) \in {\bf R},i=1,...,n$. Now define $$v^* = r_1u_1^* + \ldots + r_nu_n^*.$$ Consider $$v^*(u_i) = r_1u_1^*(u_i) + \ldots + r_nu_n^*(u_i) = r_i.$$ So $u^*$ and $v^*$ match on the elements of the basis of $V$. Thus $u^*=v^*$. $\blacksquare$
Conclusion 1: $$\dim V^* = \dim V = n.$$
So by the Classification Theorem of Vector Spaces, we have
Conclusion 2: $$V^* \simeq V.$$
A two-line version of the proof: $V$ with basis of $n$ elements $\simeq {\bf R}^n$. Then $V^* \simeq {\bf M}(1,n)$. But $\dim {\bf M}(1,n)=n$, etc.
Even though a space is isomorphic to its dual, their behavior is not "aligned" (with respect to linear operators), as we show below. In fact, the isomorphism is dependent on the choice of basis.
Note 1: The relation between a vector space and its dual can be revealed by looking at vectors as column-vectors (as always) and covectors as row-vectors: $$V = \left\{ x=\left[ \begin{array}{} x_1 \\ \vdots \\ x_n \end{array} \right] \right\}, V^* = \{y=[y_1,\ldots,y_n]\}.$$ This way we can multiply the two as matrices: $$xy=[y_1,\ldots,y_n] \left[ \begin{array}{} x_1 \\ \vdots \\ x_n \end{array} \right] = [y_1,\ldots,y_n][x_1,\ldots,x_n]^T =x_1y_1+...+x_ny_n.$$ The result is their dot product which can also be understood as a linear operator $y\in V^*$ acting on $x\in V$.
Note 2: $$\dim \mathcal{L}(V,U) = \dim V \cdot \dim U,$$ if the spaces are finite dimensional.
Exercise. Find and picture the duals of the vector and the covectors depicted in the first section.
Exercise. Find the dual of ${\bf R}^2$ for two different choices of basis.
Operators and naturality
That's not all.
We need to understand what happens to a linear operator $$A:V \rightarrow W$$ under duality. The answer is uncomplicated but also unexpected, the corresponding dual operator goes in the opposite direction: $$A^*:W^* \rightarrow V^*!$$ And not just because this is the way we chose to define it: $$A^*(f)=f \circ A.$$ A dual counterpart of $A$ really can't be defined in any other way. Consider: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & V & \ra{A} & W \\ & _{g \in V^*} & \searrow & \da{f \in W^*} \\ & & & {\bf R} \end{array} $$ If this is understood a commutative diagram, the relation between $f$ and $g$ is given by the equation above. So, we get $g$ from $f$ by $g=fA$, but not vice versa.
Note. The diagram also suggests that the reversal of the arrows has nothing to do with linearity. The issue is "functorial".
Theorem. For finite dimensional $V,W$, the matrix of $A^*$ is the transpose of that of $A$: $$A^*=A^T.$$
Proof. Exercise. $\blacksquare$
The composition is preserved but in reverse:
Theorem. $(AB)^*=B^*A^*.$
Proof. $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & V & \ra{A} & W & \ra{B} & U\\ & _{g \in V^*} & \searrow & \da{f \in W^*} & \swarrow & _{h \in U^*} \\ & & & {\bf R} \end{array} $$
Finish (Exercise.) $\blacksquare$
As you see, the dual $A^*$ behaves very much like but is not to be confused with the inverse $A^{-1}$. Of course, the former is much simpler!
The isomorphism $D$ between $V$ and $V^*$ is very straight-forward: $$D_V(u_i)=u_i^*,$$ where $\{u_i\}$ is a basis of $V$ and $\{u^*_i\}$ is its dual. However, because of the reversed arrows the isomorphism isn't "natural". Indeed, if $f:V \rightarrow U$ is linear, the diagram below does not commute, in general: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & V & \ra{f} & U \\ & \da{D_V} & \ne & \da{D_U} \\ & V^* & \la{f^*} & U^*\\ \end{array} $$
Exercise. Why not?
However, the isomorphism with the "second dual" $V^{**}=(V^*)^*$ is natural: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llllllllllll} & V & \ra{f} & U \\ & \da{D_V} & & \da{D_U} \\ & V^* & & U^*\\ & \da{D_{V^*}} & & \da{D_{U^*}} \\ & V^{**} & \ra{f^{**}} & U^{**}\\ \end{array} $$
Exercise. Prove that. Demonstrate that it is independent from the choice of basis.
When the dot product above is replaced with a particular choice of inner product, we have an identical effect. A general term related to this is adjoint operator.
A major topological application of the idea is in chains vs cochains.
Change of basis
The reversal of arrows also reveals that a change of basis of $V$ affects differently the coordinate representation of vectors and covectors.