Robustness of topology: persistence

Vietoris-Rips construction

Here's one approach...

Given $r>0$, we deem any two points that lie within $r$ from each other as "close". In this case, this pair of points is connected by an edge. Further, if three points are "close", pairwise, to each other, we add a face spanned by these points. If there are four, we add a tetrahedron, and, finally, any $d+1$ "close" points create a $d$-cell.

The result is a simplicial complex $K$ for each $r$.

Together, they form a sequence called filtration as a sequence of "nested" simplicial complexes: $$K¹ ↪ K² ↪ K³ ↪ K⁴ ↪ … ↪ K^s,$$ where the arrows are the inclusions.

In order to understand the topology of the object that produced the filtration we look at a sequence of homology groups connected by homomorphisms: $$H_{\ast}(K^{1})\rightarrow H_{\ast}(K^{2})\rightarrow\ldots\ \rightarrow H_{\ast}(K^{s})\longrightarrow 0, $$ generated by this sequence.

This is the homology.

Dimension $0$: $${\bf Z}\times {\bf Z}\rightarrow {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z} \rightarrow 0. $$ Dimension $1$: $$0\rightarrow 0 \rightarrow {\bf Z} \rightarrow {\bf Z} \rightarrow 0 \rightarrow 0. $$

Exercise: Find the homology of the inclusions.

A similar construction is possible that uses the density of points instead of the distances.

Analysis

While constructing a simplicial complex from a point cloud we gradually add cells of various dimensions in order to discover the topology of the object.

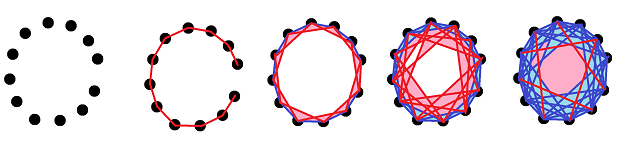
For example, this is what a point cloud of a circle might look like:

But how do we know which one of these complexes is the "true" representation without looking at it?

Or, more narrowly, which one captures the hole of the circle, without us looking at it to confirm?

To answer this question we look at the whole sequence and how it is developing.

To evaluate the topology one has to take into account the robustness of the topological features in such a sequence. Recall, a filtration is a sequence of "nested" cell complexes, where the arrows are inclusions: $$K^1↪K^2↪K^3↪...↪K^s.$$

The measurement for this robustness is called persistence.

Example

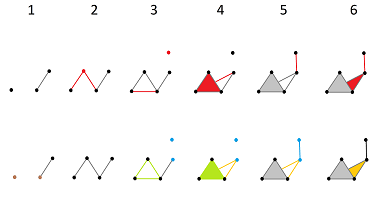
Let's consider a simpler example:

In the top row we see the complexes of the filtration. In each "frame", the new cells are marked in red.

In the bottom row, the new cycles are given in various colors.

• The brown $0$-cycle appears in the 1st frame and dies in the 2nd.
• The blue $0$-cycle appears in the 3rd frame and dies in the 5th.
• The green $1$-cycle appears in the 3rd frame and dies in the 4th.
• The orange $1$-cycle appears in the 4th frame and dies in the 6th.

The persistence a homology class can be evaluated as its life-span: how long does it take for these cycles to disappear.

Therefore, the persistences of the above cycles are 1, 2, 1, 2, respectively.

Now, in order to settle on a particular topology we choose a threshold for persistence. If the choice is 1, then the "persistence homology" of the filtration is generated by two $0$-cycles and two $1$-cycles. If, however, the choice is $2$, there is only one of each.

Which is the "correct" one, is still a judgement call.

Why is this a fruitful idea? Because this way we deal with ambiguity in a purely topological way.

Definition

Now, what about homology groups?

Let's look at the homology groups of the elements of the filtration.

Dimension $0$ homology groups: $${\bf Z}\times {\bf Z}\rightarrow {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z} \rightarrow {\bf Z}. $$ These tell the whole story; cycles appear and disappear and the homology groups change accordingly.

Dimension $1$ homology groups: $$0\rightarrow 0 \rightarrow {\bf Z} \rightarrow {\bf Z} \rightarrow {\bf Z} \rightarrow 0. $$ These don't tell the whole story; it is impossible to deduce that one cycle appeared and another disappeared at the same time! The persistence information is lost.

Recall that the $k$th homology group of \(K^{i}\) is defined as $$H_{k}(K^{i})=Z_{k}^{i}/B_{k}^{i},$$ where

• \(Z_{k}^{i}\) is the group of k-cycles in \(K^{i}\) and
• \(B_{k}^{i}\) is the group of k-boundaries in \(K^{i}\).

Now, we are trying to capture the cycles that appear, as cycles, in $i$th complex and were killed, as boundaries, in the $(i+p)$th.

Given a positive integer $p$, the $p$-persistence $k$th homology group of $\{K^{i}\}$ is $$H_{k}^{i,p}(K^{i})=Z_{k}^{i}/(B_{k}^{i+p}∩Z_{k}^{i}).$$

The persistent Betti numbers are the ranks of the persistent homology groups.

For a better analysis one will need homology maps of the inclusions.

Experiment with a dataset

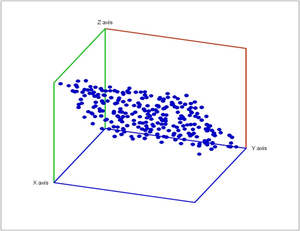
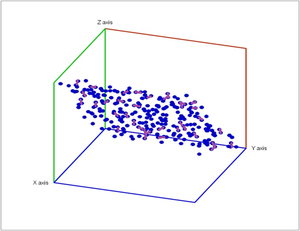
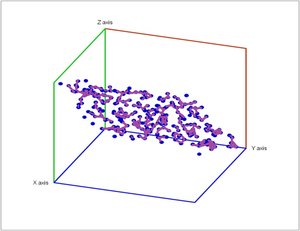
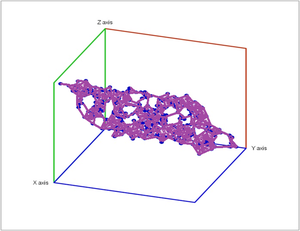
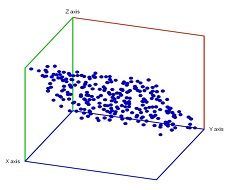
Below is an example of how we determine the persistent Betti numbers of a point cloud computed with the homology software called JPlex.

Specifically, noise has been added to a point cloud of the plane in space.

In these diagrams we provide the lifespans of the cycles called barcodes:

We can see that there is one cycle in dimension $0$ that has a much longer lifespan than others. So the set probably connected!

In dimension $1$, no single feature persists significantly. So it's probably simply connected!

In image analysis persistent Betti numbers of 2d gray scale images with respect to the filtration created by thresholding and, in this case,

persistence = contrast.

The stability of topology in the presence of noise is called persistence.

The analysis is based on the concept of filtration, which is a sequence of "nested" cell complexes, where the arrows are inclusions: $$K^1↪K^2↪K^3↪...↪K^s.$$ Then we have a sequence of homology groups connected by homomorphisms: $$H_{∗}(K¹)→H_{∗}(K²)→… →H_{∗}(K^{s})→0.$$

Previously we defined persistent homology on the chain level. It is easier to understand on the homology level, how long does it take for the homology operators to "kill" the given homology class?

Example

Previously we have considered persistence of homology classes in filtrations for this example, on the chain level:

This time we look at the homology classes specifically. The persistence of a homology class can be evaluated as its life-span: how many applications of the homology operators of the inclusions does it take for the homology class to become $0$.

• The brown $0$-class appears in the 1st frame and dies in the 2nd, persistence 1.
• The blue $0$-class appears in the 3rd frame and dies in the 5th, persistence 2.
• The green $1$-class appears in the 3rd frame and dies in the 4th, persistence 1.
• The orange $1$-class appears in the 4th frame and dies in the 6th, persistence 2.

Since we don't want to look at one class at a time, let's look at the homology groups (over ${\bf R}$) and the homology operators of the whole filtration.

• Dimension $0$:
  • homology groups: $${\bf R}\times {\bf R}\rightarrow {\bf R} \rightarrow {\bf R}\times {\bf R} \rightarrow {\bf R}\times {\bf R} \rightarrow {\bf R} \rightarrow {\bf R}. $$
  • homology maps: $$[1,1], [1,0]^T, Id, [1,1], Id.$$
• Dimension $1$:
  • homology groups: $$0\rightarrow 0 \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow 0. $$
  • homology maps: $$0, 0, [0,1]^T, Id, 0.$$

Now, the definition of the persistent homology of a complex $K^i$ in the filtration is clear:

• the $0$-persistence homology is simply its homology group;
• the $1$-persistence group is the orthogonal complement of the kernel of the homology map of the inclusion of the complex into the next one;
• the $2$-persistence group is the orthogonal complement of the kernel of the homology map of the composition of the two inclusions;
• etc.

Exercise. Compute the persistent homology groups of this filtration.

Later we define a single group that captures all information about the homology of the filtration.

A different kind of example

Consider, in contrast, an example from digital image analysis.

Here, a binary picture of a real-life object is taken with a higher and higher resolution. The result is a sequence of cubical complexes, which can one again call a filtration. At step $n$, one assigns a given pixel to complex $K_n$, if the image of the object crosses it. As a result we have a decreasing sequence of complexes: $$K_1\supset K_2\supset ... \supset K_n . $$ In fact, if we choose the resolution of the last image to apply to all images, this a sequence of subcomplexes of $K_1$!

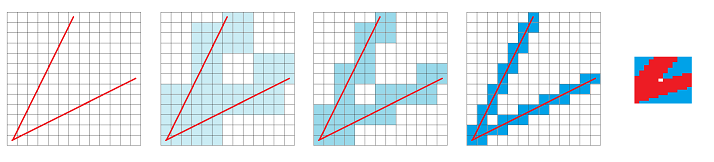
It is tempting to conclude that each topological feature in the space being discretized is captured by at least one of the elements of the filtration. The example below shows that this isn't always the case:

Here we discretize a V-shaped figure (left) with $3\times 3$, $2\times 2$, and $1\times 1$ grids. In each case the result is topologically the same:

• one component, and
• one hole.

Of course, there is no hole in the original!

It is clear that improving the resolution won't change the result. In fact the last image on the right shows the left bottom pixel zoomed in and a disconnected pixel (hole) is still present.

Now, these three images -- going from right to left -- form a filtration.

The bad news is that the homology, $H_1(K^i),i=1,2,3$, produced by this filtration are identical and the hole might appear -- incorrectly -- persistent.

The good news that with a help of the homology maps the issue is resolved. At every step, the hole goes to zero under the homology operator of the inclusion. Therefore the persistence of each of the holes is equal to 1!

Experiments

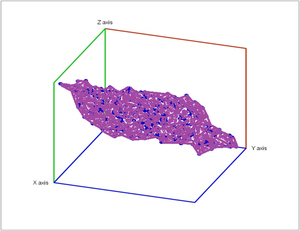
Below is an example of how we determine the persistent Betti numbers of a point cloud computed with JPlex. To be precise, these are relative Betti numbers, i.e., the edges are identified (see quotient spaces).

Below noise has been added to a plane in space.

In addition to computing the Betti numbers as the global topological characteristics of the complex, homology theory can also provide local information. For every small patch $P$ of $K$ we compute the relative homology $H_{\ast}(K,K\backslash P)$ by, essentially, collapsing the complement of $P$ to a single point. Then, if $K$ is a manifold, its dimension is equal to $n$ provided:

• $H_{n}(K,K\backslash P)\neq0$ and
• $H_{k}(K,K\backslash P)=0$ for $k\neq n.$

In the above barcodes, we see the following.

• In dimension $0$, one feature persists longer that other dimension $0$ features.
• In dimension $1$, no single feature has a particularly long lifespan compared to other dimension $1$ features.
• In dimension $2$, one features has a significant lifespan.

By analyzing the barcodes of relative Betti numbers, we determine the dimension of our data set. In this example, the persistent Betti numbers are: $$B_0 = 1, B_1 = 0, B_2 = 0, …$$ Thus the data set constitutes a single part, and has no other topological features. Next, the persistent relative Betti numbers are: $$B_0 = 1, B_1 = 0, B_2 = 1, B_3 = 0, …$$ The result confirms that the data set is two-dimensional.

Project: Create a digital geometric figure with no symmetries, create the dataset of all photos (or, alternatively, the projections) from all possible directions, evaluate the homology of the dataset with JPlex. The homology produced this way is supposed to coincide with

• either the homology of the sphere ${\bf S}^2$:

$$H_1({\bf S}^2)=0,H_2({\bf S}^2)={\bf Z};$$

• or the homology of the rotation group $SO(3)$:

$$H_1(SO(3);{\bf Z})={\bf Z}_2.$$