Filtration

Filtration is a sequence of "nested" sets, topological spaces, cell complexes, cubical complexes etc: $$K¹ ↪ K² ↪ K³ ↪ K⁴ ↪ … ↪ K^s,$$ where the arrows are the inclusions.

Below is an example of a gray scale image and its three thresholded versions. These are binary images that can be understood as cell complexes (see Cell decomposition of images). Here white is empty.

For completeness sake one can add a fully white image in the beginning and fully black in the end.

Another example:

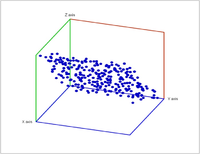
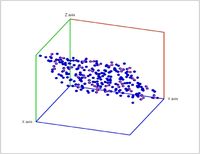
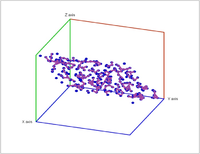
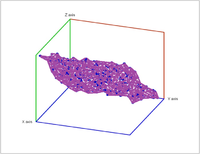
Another source of filtrations comes from "enlarging" a point cloud that results in a Vietoris-Rips complex:

For topological analysis of filtrations see Persistent homology.

There can also be multi-parameter filtrations, see Color images.