This site is being phased out.
Homology of cubical complexes
Redirect to:
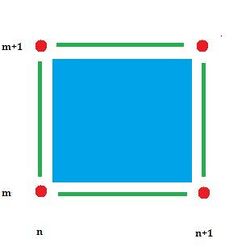
A cubical complex is a collection of cells on a grid. If this is a 2D grid, we define cells as follows:
- a vertex is a $0$-cell, $\{n \} \times \{m \}$,
- an edge is a $1$-cell, $\{n \} \times (m, m + 1)$ or $(n, n + 1) \times \{m \}$,
- a pixel is a $2$-cell, $(n, n + 1) \times (m, m + 1)$.
Boundaries of the cells are chains; chains are simply arbitrary combinations of cells (and possibly $0$):
- $\partial \{(n, m) \} = 0;$
- $\partial \{n \} \times (m, m + 1) = \{(n, m) \} + \{(n, m + 1) \}$
- $\partial (n, n + 1) \times \{m \} = \{(n, m) \} + \{(n + 1, m) \};$
- $\partial (n, n + 1) \times (m, m + 1)$
$= (n, n + 1) \times \{m \} + \{n \} \times (m, m + 1) + (n, n + 1) \times \{m + 1 \} + \{n + 1 \} \times (m, m + 1).$
Chains can combine cells of any dimension but if all cells are $k$-dimensional, then the chain is also called $k$-dimensional, or a $k$-chain. So the boundaries of $k$-cells are $(k-1)$-chains. Moreover, the boundaries of $k$-chains are $(k-1)$-chains.
Exercise. Compute the boundaries of a 3D cell in a 3D grid.
Definition. Given a chain $$s = a_1 + a_2 + ... + a_n,$$ where $a_1, a_2, \ldots a_n$ are cells, the boundary $\partial s$ of $s$ is given by $$\partial s = \partial a_1 + \partial a_2 + \ldots + \partial a_n.$$
In the computations we follow this algebraic rule of cancellation: $$2x = 0.$$ In other words if a cell appears twice in a chain, it is canceled.
The reason for this rule will become clear when we look at homology in a more algebraic way (see Homology). The illustration below suggest what that reason is.
Example. Boundary of the chain representing two adjacent edges is $$\begin{array}{} \partial ( \{n \} \times (m, m + 1) + (n, n + 1) \times \{m \} ) &= \partial \{n \} \times (m, m + 1) + \partial (n, n + 1) \times \{m \} \\ &= \{(n, m) \} + \{(n, m + 1) \} + \{(n, m) \} + \{(n + 1, m) \} \\ &= \{(n, m + 1) \} + \{(n + 1, m) \} \end{array}$$
Only the end points left, as expected.
Example. Boundary of a curve: $$\begin{array}{} \partial (a + b + c + g + f) &= A + B + B + C + C + F + F + E + E + D {\rm (cancellation)} \\ &= A + D. \end{array}$$
Only the end points remain, as expected.
Example. The boundary of the boundary of a $2$-cell: $$\begin{array}{} \partial \partial (n, n + 1)×(m, m + 1) \\ = \partial ( (n, n + 1) \times \{m \} + \{n \} \times (m, m + 1) + (n, n + 1) \times \{m + 1 \} + \{n + 1 \} \times (m, m + 1) ) {\rm (compute)} \\ = 0. \end{array}$$
Exercise. Check the computation above.
Theorem. $$\partial \partial = 0.$$
In other words, boundaries have no boundaries.
For more details see Chain complexes.
Among all the chains, we are interested firstly in the ones that capture topological features: components, tunnels, voids etc.
Consider tunnels (holes in 2D). As we saw previously, tunnels are captured by closed curves. Such a curve can certainly be made of just the edges ($1$-cells) followed consecutively until you come back to the first vertex. What is so special about such a collection of edges? Every edge has another one attached to its end points by its initial point. Therefore each vertex appears twice. If the curve revisits the vertex one more time, then the vertex appears four times, etc. Thus each vertex appears, as an end point of an edge, an even number of times. Therefore the boundary of this chain is $0$.
So, the algebraic analogue of a closed curve is a chain with $0$ boundary.
Definition. A chain $C$ is called a cycle if $$∂C = 0.$$
If $C$ is a $k$-chain, we call it $k$-cycle.
Since the boundary of any $0$-cell is $0$, all $0$-chains are cycles. As we just showed, $1$-cycles correspond to closed (parametric) curves. A similar argument will show that $2$-cycles correspond to closed (parametric) surfaces.
Since there are many chains that capture the same topological feature, we combine them into equivalence classes. The way it was done previously:
- two points are homologous if they are the end points of a curve.
- two closed curves are homologous if they form a boundary of a surface.
- two closed surfaces are homologous if the are the boundary of a solid.
This time everything is entirely algebraic.
Definition. Two $k$-cycles $A$ and $B$ are homologous $(A \sim B)$ if they are the boundary of a $(k+1)$-chain: $$∂C = A + B.$$
Example.
Dimension 0: Two $0$-cycles are homologous if there is a path between them made of edges.
Dimension 1: Two $1$-cycles are homologous if there is a chain connecting them made of faces.
Dimension 2: Exercise...
Exercise. Prove that for a $1$-chain $a$, $\partial a=0$ iff $a$ is a closed curve (i.e., $1$-cycle). Solution: 
Exercise. Show that homology is an equivalence relation.
Now, each homology class captures a single topological feature of the complex in each dimension.
Definition. The $k$-th homology $H_k(K)$ of complex $K$ is the set of all $k$-homology classes of $K$.
We can also write $$H_k(K) = H_k(|K|) = H_k(X).$$
The homology class of the trivial chain $0$ is denoted by $0$. We include it in $H_k(K)$. It is a matter of convenience for now but in the future this becomes crucial as we treat the homology as a group.
Exercise. Show that for any $0$-chain $A$, $A \sim 0$ if and only if $A = 0$.
Exercise. Compute the homology of the complex on the right. Solution: 
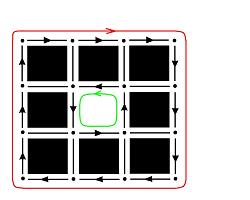
Exercise. Prove that for any cubical complex $K$, $H_0(K)$ has only one non-zero element if and only if its realization $|K|$ is (path) connected. (Note that in the case of path connectedness, the points being connected don't have to be vertices and the path doesn't have to be made of edges. Illustration: 
) Hint: Think of edges as streets, vertices as intersections, cells as parking lots, $0$-homology as a turn-by-turn instructions from an intersection to another. Solution: 
Theorem. Homology is a topological invariant.
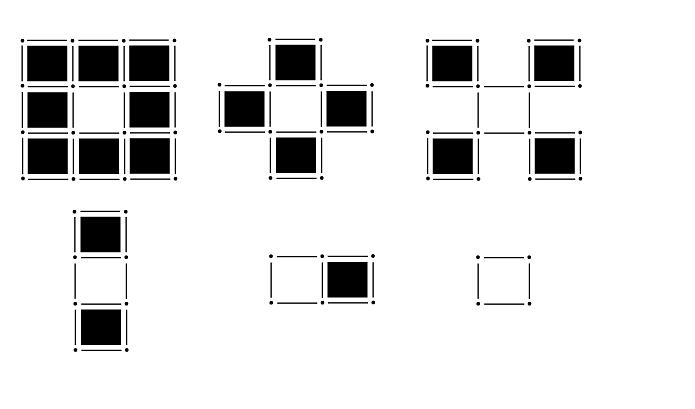
To illustrate, the homology of the six complexes below is the same, that of the circle.
Proving theorems like this requires some build-up: Introduction to point-set topology and Homology theory.
In the presence of noise one has to consider persistent homology.
To see how Pixcavator captures $0$- and $1$-homology classes in digital images, continue to Cycles. See also Homology software and Image analysis software.
