This site is being phased out.
Homology as a group
Redirect to:
For an initial discussion, see The algebra of chains.
If you look at homology as a vector space, the chains are linear combinations of cells. And by linear combinations we always mean (in linear algebra), the ones with real coefficients, such as:
But, we can also consider linear combinations with coefficients in any ring $R$: $$p \varsigma + q \sigma + r \tau, p,q,r \in R.$$
The algebra is the same.
For example, initially one can "ignore" coefficients and consider the "unions" (or "combinations" etc) rather than sums of cells. For the algebra to work with the topology, however, one has to add the "cancellation rule": $$\sigma + \sigma = 0.$$ Rephrased this means $$2 \sigma = 0,$$ or $$2 = 0.$$ We discover that we deal with the same kinds of chains but the coefficients are binary!
Note: Since ${\bf Z}_2$ is a field, the homology group is still a vector space.
Let's review how we construct the homology for ${\bf R}$ and compare the process for ${\bf Z}$. We will have $${\bf R} \rightsquigarrow {\bf Z}$$ every time we make the switch.
Given a finite cell complex $K$.
A chain is a "formal" linear combination of (oriented) cells. Let $C_k(K)$ denote the set of all chains: $$C_k(K) = \left\{ \displaystyle\sum_i s_i \sigma_i \colon s_i \in {\bf R} \rightsquigarrow {\bf Z}, \sigma_i {\rm \hspace{3pt} is \hspace{3pt} a \hspace{3pt}} k{\rm -cell \hspace{3pt} in \hspace{3pt}} K \right\}.$$
We define addition of chains by adding the coefficients of each cell: $$A = \displaystyle\sum_i s_i \sigma_i,B = \displaystyle\sum_i t_i \sigma_i,$$ then $$A + B = \displaystyle\sum_i ( s_i + t_i) \sigma_i.$$
Theorem. $C_k(K)$ is a vector space $\rightsquigarrow$ group with a basis $\rightsquigarrow$ generator set which consists of the $k$-cells of $K$.
The boundary operator is a linear operator $\rightsquigarrow$ homomorphism.
A chain is called a cycle if its boundary is $0$.
Theorem. The cycles form a subspace $\rightsquigarrow$ subgroup $Z_k(K)$, the $k$-cycle group, of the chain group $C_k(K)$ which is the kernel of the boundary operator: $$Z_k(K) = {\rm ker \hspace{3pt}} \partial.$$
A $k$-chain is called boundary if it's the boundary of a $(k+1)$-chain.
Theorem. The boundaries form a subspace $\rightsquigarrow$ subgroup $B_k(K)$, the $k$-boundary group of the chain group $C_k(K)$ which is the image of the $(k+1)$-chain group under the boundary operator: $$B_k(K) = \partial (C_{k+1}(K)).$$
Theorem. Every boundary is a cycle: $$\partial \partial = 0.$$
So, the boundary group is a subspace $\rightsquigarrow$ subgroup of the cycle group.
Up until this point the difference between homology over ${\bf R}$ and homology over ${\bf Z}$ is negligible. The only change has been this: $${\bf R}^n \rightsquigarrow {\bf Z}^n.$$ The algebra is the same so far.
This simplicity disappears as soon as we introduce quotients into the picture!
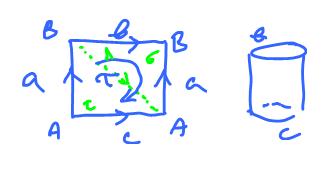
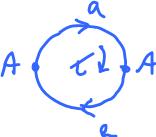
Consider the boundary group of the cylinder.
These are the chain groups generated by the cells: $$\begin{array}{l} C_2(K) &= {\rm span}\{ \tau \} &\rightsquigarrow < \tau >, \\ C_1(K) &= {\rm span}\{a, b, c \} &\rightsquigarrow < a, b, c >. \end{array}$$
Next, these are the cycle group and the boundary group: $$\begin{array}{l} Z_1(K) = {\rm span}\{b, c \} \rightsquigarrow < b, c >, {\rm \hspace{3pt} and} \\ B_1(K) = {\rm span}\{ \partial \tau \} = {\rm span}\{a + b - a - c \} = {\rm span}\{ b - c \} &\rightsquigarrow < b - c >. \end{array}$$
This last part is understood as $$b - c \sim 0,$$ and $$B - A \sim 0. $$ Algebraically, $$x \sim y {\rm \hspace{3pt} iff \hspace{3pt}} x - y \in B_1(K).$$ (See Quotients of groups. )
Thus the homology group is a vector space $\rightsquigarrow$ group that is the quotient of the cycles over the boundaries: $$H_k(K) = Z_k(K) / B_k(K).$$
For the cylinder: $$H_1(K) = {\rm span}\{b, c \} / {\rm span}\{ b - c \} = {\rm span}\{ b + {\rm span}\{ b - c \} \} \rightsquigarrow < [b] >.$$
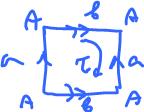
Let's consider the torus:
$$\begin{array}{l} Z_1(K) = {\rm ker \hspace{3pt}} \partial = {\rm span}\{a, b \} &\rightsquigarrow < a, b >, \\ B_1(K) = {\rm span}\{ \partial \tau \} = {\rm span}\{a + b - a - b \} = {\rm span}\{0 \} = 0 &\rightsquigarrow < 0 > = 0, {\rm \hspace{3pt} so} \\ H_1(K) = {\rm span}\{a, b \} / 0 = {\rm span}\{a, b \} \rightsquigarrow < a, b >. \end{array}$$
The $k$-th Betti number is the dimension $\rightsquigarrow$ the rank of the $k$-th homology group: $$b_k(K) = {\rm dim \hspace{3pt}} H_k(K) \rightsquigarrow {\rm rank \hspace{3pt}}H_k(K).$$
What works easily, however, for linear algebra and their dimensions: $${\rm dim \hspace{3pt}} L / M = {\rm dim \hspace{3pt}} L - {\rm dim \hspace{3pt}} M,$$ does not work for groups and their ranks. The difference is in the possibility of torsion!
Let's consider the homology of the projective plane ${\bf P}^2$:
- $2$-cells: $\tau$ with $\partial \tau = 2a$;
- $1$-cells: $a$ with $\partial a = 0$;
- $0$-cells: $A$ with $\partial A = 0$.
Here $a$ is a cycle but not a boundary!
- $C_1 = < \tau >$,
- $B_1 = {\rm im \hspace{3pt}} \partial = < \partial \tau > = < 2a >,$
- $Z_1 = {\rm ker \hspace{3pt}} \partial = < a >.$
The mismatch between the last two creates the torsion in the homology: $$H_1 = < a > / < 2a > = {\bf Z} / 2{\bf Z} = {\bf Z}_2.$$ It is generated by [2a].
The crucial conclusion is that this feature is left undetected by the homology over a field!
Exercise. Compute the homology of the Klein bottle over ${\bf Z}$, notation: $$H_*({\bf K}^2; {\bf Z}).$$
Exercise. Let $P$ be a polygon with $n$ vertices $v_0,...,v_{n-1}$ adjacent to each other in this order around $P$. Suppose the edges of $P$ are oriented in this order. Now, suppose these edges are glued together. This quotient space $Q$ is called the $n$-fold dunce cap. Prove that $$H_1(Q)={\bf Z}_n .$$