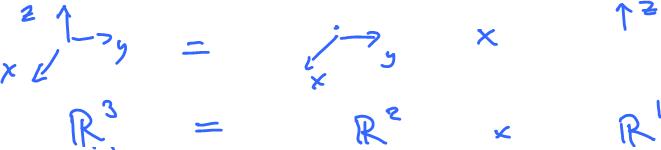This site is being phased out.
Products of vector spaces
From Mathematics Is A Science
Jump to navigationJump to searchGiven two vector spaces L and M. Define the product L×M as the product of sets, set of all pairs (a,b) of elements in X and Y respectively, as a vector space with the operations
(a,b) + (a',b') = (a + a',b + b') and t(a,b) = (ta,tb).
The projections pL: L×M → L and pY: L×M → M, pL(a,b) = a, pM(a,b) = b, are linear operators.
Theorem. (1) The bases of L and M form a basis of L×M. (2) There is a basis of L×M that consists of bases of L and M.