Mass as an integral

We need integrals to compute volumes of complicated figures and the mass of objects with non-uniform density.

We can certainly compute the volume of a box in any dimension but what about the ball, cylinder etc. Meanwhile the mass of even a simple figure isn't easy to compute unless it's made of uniform material.

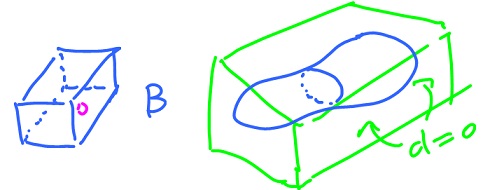
Suppose we have a (real) box B filled with stuff of varied density. Mathematically, the situation is captured by a function

 d: B → ℝ+,

and d( x, y, z ) is the density at the point ( x, y, z ).

What is the mass of B? Consider little cubes, each of volume ∆V, then estimate the density of each cube by

 d( ei, dj, el ), 

where ( e_i, d_j, e_l ) is a point in a cube. Then the estimated mass is

 ∑i,j,l d( ei, dj, el ) ∆V,   

which we recognize as a Riemann sum. It converges, as k → 0, to

 ∫∫∫B d( x, y, z) dV.

Note: we can compute the volume of a complex figure G by putting it in a box and setting the density equal to zero in the complement B\G of G.

Example. Let

 R = [ 0, 1 ] × [ 1, 2 ]. 

Then what is

 ∫∫R ( x2 y ) dA?

We can reduce the above definite integral to indefinite integrals (i.e. antiderivatives), just like in Calc 1. Except now we have two variables. of x and y.

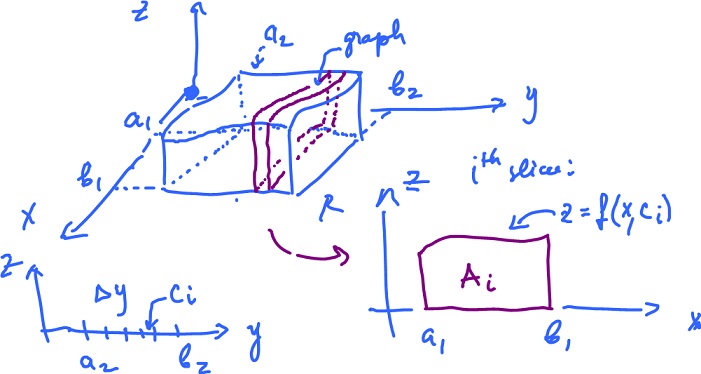
The idea is to cut the region into slices and compute the volume of each as a single integral, then add them.

Subdivide

 ∆y = ( b2 - a2 ) / k.

Suppose

 the area of the i-th slice is Ai. 

Then the volume equals the sum of the volumes of the slices, which is approximately

 V ≈ ∑i=1k Ai ∆y

(i.e. the area of the cross section multiplied with the thickness). Find, by the Fundamental Theorem of Calculus,

 Ai = ∫[a1,b1] f( x1, ci ) dx
    = ∫a1b1 f( x1, ci ) dx,

substitute:

 volume ≈ ∑i=1k ( ∫a1b1 f( x1, ci ) dx ) ∆y
 volume = limk→∞ ∑i=1k [ ∫a1b1 f( x1, ci ) dx ] ∆y.

The sum in the above formula is a Riemann sum with respect to y on [ a₂, b₂ ], but of what? Compare the above to

 limk→∞ ∑i=1k g( ci ) ∆y = ∫a2b2 g(y) dy.

What is g?

 g(y) = ∫a1b1 f( x, y ) dx.

The limit is the Riemann integral:

 volume = ∫a2b2 ∫a1b1 f( x, y ) dx dy.

These are definite integrals (dimension 1). They are computed by the FTC. For our specific function we have:

        = ∫01 ( ∫01 x2 y dx ) dy
        = ∫01 ( 1 / 3 x3 y |x=0x=1 ) dy
        = ∫01 ( 1 / 3 y - 0 ) dy 
        = y2 / 6 |01 = 1 / 6.