This site is being phased out.
Riemann integral
In the simplest settings we deal with $$f: [ a, b ] → ℝ$$ continuous. Then Riemann integral defines "the area under the graph of $f$".
Note: This makes sense in dimension 3 - volume under the surface and in dimension n:
- let $f: n-dim$ box $→ ℝ$ be scalar function, then
- graph $f ⊂ ℝ^{n+1}$.
Then it makes sense to talk about the $(n+1)$-dimensional volume "under the graph" of $f$.
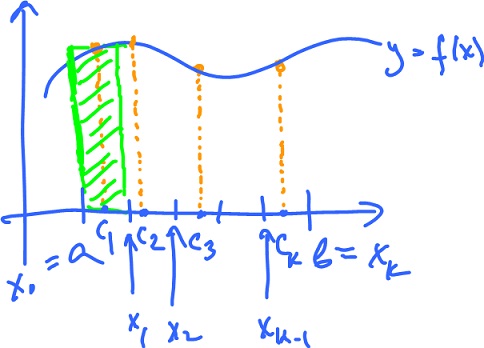
The idea is to approximate the area with rectangles.
- Pick $k$, the number of intervals.
- Cut $[a,b]$ into $k$ intervals of equal length:
- $a = x_0 < x_1 < ... < x_k = l$.
- Pick a point in each: $c_1, ..., c_k$.
- Evaluate $f$ at $c_1, ..., c_k$. These numbers are the heights of rectangles, while the bases are $[ x_i, x_{i+1}], the intervals.
- Calculate the areas of the rectangles and add them up:
- widths of rectangles $∆x = ( b - a ) / k$,
- heights of rectangles $f( c_1), ..., f( c_k)$.
- Then we get
called the Riemann sum of $f$ for this partition of $[ a, b ]$.
Consider $$\lim _{k→∞} ∑_{i=1}^k f( c_i ) ∆x$$ (or $lim_{∆x→0} ...), where $c_i$ denotes the midpoint of the respective intervals. If this limit exists, it is called the Riemann integral of $f$ from $a$ to $b$. We write $$∫_a^b f(x) dx,$$ and call $f$ an integrable function on $[ a, b ]$.
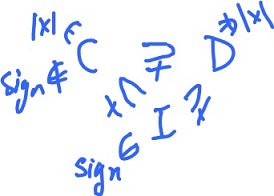
The relation of the sets of functions that are
- differentiable functions
- continuous functions
- integrable functions,
is shown on the right. The absolute value and the sign functions are the counterexamples.
Example. Let's compute something. Let
- $f(x) = x, a = 0, b = 1$, and
- $x_i = (1 / k) i$ the endpoints for $i = 1, ..., k$ ($k$ intervals).
- $c_i = (1 / k) i$ chosen points for $i = 0, ..., k-1$.
Then $$\lim _{k→∞} ∑ _{i=1}^k f( c_i ) ∆x$$ $$ = \lim_{k→∞} ∑_{i=1}^k c_i ∆x$$ $$ = \lim_{k→∞} ( c_1 + ... + c_k ) 1 / k$$ $$ = \lim_{k→∞} ( 0 + (1 / k) + (2 / k ) + ... + (( k - 1 ) / k ) k$$ $$ = \lim_{k→∞} ( (1 / k^2) + (2 / k^2) + ... + (( k - 1 ) / k^2) ) \text{ (arithmetic progression)} $$ $$ = ( k ( k - 1 ) / 2 ) / k^2$$ $$ = 1 / 2.$$ So, $$ ∫_{[0,1]} x dx $$ $$ = ∫_0^1 x dx $$ $$ = ( x^2 / 2 )|_0^1 $$ $$ = 1 / 2.$$