Homology maps

Cubical maps

Given a map $f \colon X \rightarrow Y$, we can trace what $f$ does to the homology classes in $X$ as they are mapped to $Y$. This is discussed in Maps and homology.

To study this issue properly, however, we need to limit our attention to $X$ and $Y$ which are realizations of cubical complexes, say $K$ and $L$: $$X = |K|, Y = |L|.$$

Then, we need an analogue of maps in this environment, i.e., given a map $f$ we build such a "combinatorial" construction involving complexes $K$ and $L$ that its "realization" is $f$.

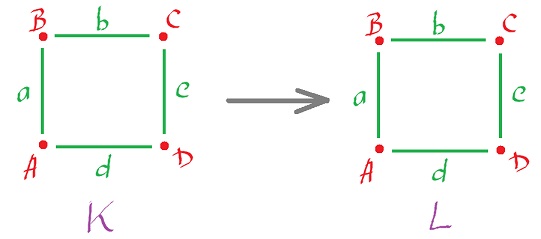
Let's consider maps of the circle to itself $$f \colon X = {\bf S}^1 \rightarrow Y = {\bf S}^1.$$

We represent $X$ and $Y$ as two identical cubical complexes $K$ and $L$ and then find an appropriate representation for $f$.

We will define function $g$ as follows:

(A) $g$ maps each cell in $X$ to a cell in $Y$ of the same dimension, or $0$.

The latter option is reserved for cells that collapse (just like homology classes collapse as discussed in Maps and homology).

Let's consider a few examples.

Identity: $$\begin{array}{l} g(A) = A, g(B) = B, g(C) = C, g(D) = D, \\ g(a) = a, g(b) = b, g(c) = c, g(d) = d. \end{array}$$

Constant: $$\begin{array}{l} g(A) = A, g(B) = A, g(C) = A, g(D) = A, \\ g(a) = 0, g(b) = 0, g(c) = 0, g(d) = 0. \end{array}$$ All $1$-cells collapse. Unlike with circles, there are only $4$ of such maps for these cubical complexes.

Flip: $$\begin{array}{l} g(A) = D, g(B) = C, g(C) = B, g(D) = A, \\ g(a) = c, g(b) = b, g(c) = a, g(d) = d. \end{array}$$ This is a vertical flip, there are also the horizontal and diagonal flips, total of $4$. Only these four axes allow condition $(A)$ to be satisfied.

Rotation: $$\begin{array}{l} g(A) = ?, g(B) = ?, g(C) = ?, g(D) = ?, \\ g(a) = ?, g(b) = ?, g(c) = ?, g(d) = ?. \end{array}$$

Exercise. How many and what are they?

Let's try this: $$g(A) = A, g(B) = C, ...$$

There is trouble. Even though we can find a cell for $g(a)$, it can't be $[A,C]$. So, $g(a)$ won't be aligned with its end-points. As a result, the "realization" of $g$ won't be continuous. To prevent this from happening we need to require that the end-points of the image of any $1$-cycle in $X$ are the images of the end-point of this cycle. To ensure the cells in all dimensions remain attached after $g$ is applied, we require:

(B) $g$ preserves boundaries.

Algebraically, $$\partial g = g \partial.$$

This condition is the cell analogue of continuity.

Observe now that $g$ is defined on complex $K$ but its values aren't all in $L$. There are also $0$s. They aren't cells, but they are chains! In fact, even though g is defined on cells of $K$ only, it can be extended to all chains, "by linearity": $$g(A + B) = g(A) + g(B), ...$$

Thus, condition $(A)$ simply means that $g$ maps $k$-chains to $k$-chains. More precisely $g$ is a collection of functions: $$g \colon C_k(K) \rightarrow C_k(L), k = 0, 1, 2, ...,$$ where $C_k(K)$ and $C_k(L)$ are the sets of all $k$-chains in $K$ and $L$ respectively. If such a function also preserves boundaries (condition $(B)$), we call it a chain operator or chain map. For brevity we use: $$g \colon C_*(K) \rightarrow C_*(L).$$

Projection: $$\begin{array}{l} g(A) = A, g(B) = A, g(C) = D, g(D) = A, \\ g(a) = 0, g(b) = d, g(c) = 0, g(d) = d. \end{array}$$

Let's verify condition $(B)$: $$\begin{array}{l} \partial g(A) = \partial 0 = 0, \\ g \partial (A) = g(0) = 0. \end{array}$$

Same for the rest of $0$-cells. $$\begin{array}{l} \partial g(a) = \partial (0) = 0, g \partial (a) = g(A + B) = g(A) + g(B) = A + A = 0. \end{array}$$

Same for $c$. $$\begin{array}{l} \partial g(b) = \partial (d) = A + D, \\ g \partial (b) = g(B + C) = g(B) + g(C) = A + D. \end{array}$$ Same for $d$.

Exercise. Try the "diagonal fold": $A$ goes to $C$, while $C, B$ and $D$ stay.

In each of these examples, an idea of a map $f$ of the circle/square was present first, then $f$ was realized as a chain map $g$ which can be denoted by $$g = f_* \colon C_*(K) \rightarrow C_*(L).$$

Next, suppose we already have a chain operator $$g \colon C_*(K) \rightarrow C_*(L),$$ what is a possible realization of $g$: $$|g| \colon |K| \rightarrow |L|?$$

The idea is simple: if we know where each vertex goes under $f$, we can construct the rest of $f$ by linearity, i.e., interpolation.

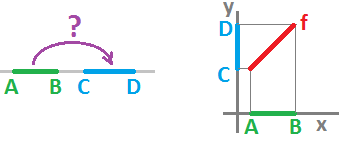
A simple example first. Suppose $$K = \{A, B, a | \partial a = A+B \}, L = \{C, D, b| \partial b = C+D \}$$ are two complexes representing the closed intervals. Define a chain operator: $$g(A) = C, g(B) = D, g(a) = b.$$

If the first two identities is all we know, we can still build a continuous function $f \colon |K| \rightarrow |L|$ such that $f_* = g$. The third identity will be taken care of because of condition $(B)$.

If we include $|K|$ and $|L|$ as subsets of the $x$-axis and the $y$-axis respectively, the solution becomes obvious: $$f(x) = C + \frac{D-C}{B-A} \cdot (x-A).$$

This approach allows us to give a single formula for realizations of all chain operators: $$f(x) = g(A) + \frac{g(B)-g(A)}{B-A} \cdot (x-A).$$

For example, suppose we have a constant map: $$g(A) = C, g(B) = C, g(a) = 0 {\rm \hspace{3pt} (collapse)}.$$ Then $$f(x) = C + \frac{C-C}{B-A} \cdot (x-A) = C.$$

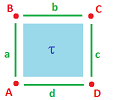
Example. Let's consider a chain map $g$ of the complex $K$ representing the "filled" square/$2$-cell.

Knowing the values of $g$ on the $0$-cells of $K$ gives us the values of $f=|g|$ at those points. How do we extend it to the rest of $|K|$?

An arbitrary point $u$ in $|K|$ is represented as a convex combination of $A, B, C, D$: $$u = sA + tB + pC + qD, {\rm \hspace{3pt} with \hspace{3pt}} s + t + p + q = 1.$$

Then we define $f(u)$ as $$f(u) = sf(A) + tf(B) + pf(C) + qf(D).$$

Thus, $f(u)$ is a convex combination of $f(A), f(B), f(C), f(D)$. But all of these are vertices of $|L|$, so $f(u) \in |L|$.

For example, suppose we are interested in the projection: $$\begin{array}{l} g(A) = A, g(B) = A, g(C) = D, g(D) = A, \\ g(a) = 0, g(b) = d, g(c) = 0, g(d) = d. \\ g(τ) = 0. \end{array}$$ Then $$\begin{array}{} f(u) &= sf(A) + tf(B) + pf(C) + qf(D) \\ &= sA + tA + pD + qD \\ &= (s+t)A + (p+q)D. \end{array}$$

Since $(s+t) + (p+q) = 1$, $f(u)$ belongs to the interval $[A,D]$. (See also Extensions.)

To summarize the algebra of chain maps consider the commutative diagram:

$$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccc} \da{\partial_3} & & \da{\partial_3} \\ C_2(K) & \ra{g_2} & C_2(L) \\ \da{\partial_2} & & \da{\partial_2} \\ C_{1}(K) & \ra{g_{1}} & C_{1}(L)\\ \da{\partial_1} & & \da{\partial_1} \\ C_{0}(K) & \ra{g_{0}} & C_{0}(L)\\ \da{\partial_0} & & \da{\partial_0} \\ 0 & & 0\\ \end{array} $$

This is an expanded version of condition $(B)$: $$\partial g = g \partial.$$

The condition indicates that each square in the diagram commutes: $$\partial_k g_{k-1} = g_k \partial_k.$$

Then, $\{C_*(K), \partial \}$ is called the chain complex of $K$. It is used to compute the homology $\{H_*(K) \}$ of $K$. Meanwhile, a chain operator is a map between chain complexes $$g \colon \{ C_*(K), \partial \} \rightarrow \{C_*(L), \partial \}$$ that preserves boundaries. It is used to compute the homology operator $$g_* \colon H(K) \rightarrow H(L).$$

Definition

Given a cell map $f \colon K \rightarrow L$, the homology operator induced by f, $$f_* \colon H_k(K) \rightarrow H_k(L), {\rm \hspace{3pt} for \hspace{3pt} all \hspace{3pt}} k,$$ is a linear operator given by $$f_*([x]) = [f_k(x)],$$ where $$f_k \colon C_k(K) \rightarrow C_k(L)$$ is the chain map.

Why is the homology well defined?

Because the chain map preserves the boundary: $$\partial_k f_{k-1} = f_k \partial_k.$$ In other words, this diagram commutes: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccc} \da{\partial_3} & & \da{\partial_3} \\ C_2(K) & \ra{g_2} & C_2(L) \\ \da{\partial_2} & & \da{\partial_2} \\ C_{1}(K) & \ra{g_{1}} & C_{1}(L)\\ \da{\partial_1} & & \da{\partial_1} \\ C_{0}(K) & \ra{g_{0}} & C_{0}(L)\\ \da{\partial_0} & & \da{\partial_0} \\ 0 & & 0\\ \end{array} $$

Examples

We've already carried out a few computations...

For dimension $k>0$:

• The identity: identity, $Id_*=Id.$
• The constant: zero, $f_*=0$.
• Self-maps of the circle:
  • flip: negative $f_*(c) = -c.$
  • turn: identity.
  • twice wound: doubling/stretch, $f_*(c) = 2c.$
• Collapse of the torus to its longitude: projection, $f_*(L) = 0, f_*(l) = c.$
• Inclusion of the circle in the plane: zero, $f_*(c) = 0.$

Exercise. Consider a few possible maps for each:

• inclusions of the circle into the torus;
• self-maps of the figure eight;
• inclusions of the circle to the sphere.

Properties

The following is obvious.

Theorem 1. The identity map induces the identity homology operator: $${\rm id}_{|K|} = {\rm id}_{H(K)}.$$

This is what we know about compositions of cell maps:

Theorem 2. The homology operator of the composition is the composition of the homology operators $$(gf)_* = g_*f_*.$$

The main result related to this theorem is below.

Theorem 3. Suppose K and L are cell complexes, if a map $$f \colon |K| \rightarrow |L|$$ is a cell map and a homeomorphism, and $$f^{-1} \colon |L| \rightarrow |K|$$ is a cell map too, then the homology operator $$f_* \colon H_k(K) \rightarrow H_k(L)$$ is an isomorphism for all $k$.

Proof. From the definition of inverse function, $$ff^{-1} = {\rm id}_{|L|},$$ $$f^{-1}f = {\rm id}_{|K|}.$$ From the above theorems, $$f_*(f^{-1})_* = {\rm id}_{H(L)},$$ $$(f^{-1})_* f_* = {\rm id}_{H(K)}.$$ $\blacksquare$

Robustness of homology

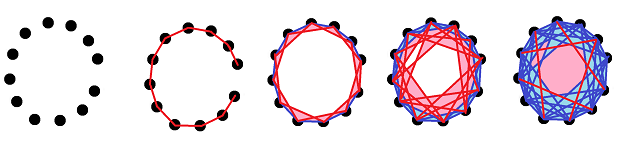
While constructing a simplicial complex from a point cloud we add cells at once or we can add them gradually -- and gradually to discover the topology of the object.

For example, this is how constructing a point cloud of a circle might look like:

But how do we know which one of these complexes is the "true" representation of data? Or, more to the point,

which complex captures the hole of the circle?

Is it even possible? How can we tell without looking at the picture to confirm?

To answer this question we consider the whole sequence and the way it develops. We also rephrase the question:

which cycle captures the hole in the circle?

A filtration is a sequence of "nested" complexes: $$K^1↪K^2↪K^3↪...↪K^s,$$ where the arrows are the inclusions. To evaluate the topology one has to take into account the robustness of the topological features in such a sequence.

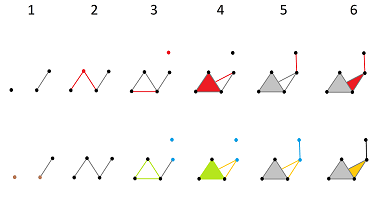
Let's consider a simpler example:

In the top row we see the complexes of the filtration, like frames in a film. In each frame, the new cells are marked in red.

In the bottom row, the new cycles are given in various colors:

• The brown $0$-cycle appears in the 1st frame and disappears in the 2nd.
• The blue $0$-cycle appears in the 3rd frame and disappears in the 5th.
• The green $1$-cycle appears in the 3rd frame and disappears in the 4th.
• The orange $1$-cycle appears in the 4th frame and disappears in the 6th.

Then the persistence of a cycle is a measurement for its robustness. It can be evaluated as the "life-span" of the cycle within this sequence: how long it takes for the cycle to disappear.

Therefore, the persistences of the above cycles are 1, 2, 1, 2, respectively.

Now, in order to settle on a particular cycle or cycles we choose a threshold for persistence. If the choice is $1$, then the "persistence homology" of the filtration is generated by two $0$-cycles and two $1$-cycles. If, however, the choice is $2$, there is only one of each.

Which is the "correct" one, is still a judgement call.

Let's now look at the homology groups of the elements of the filtration.

Dimension $0$ homology groups: $${\bf R}\times {\bf R}\rightarrow {\bf R} \rightarrow {\bf R}\times {\bf R} \rightarrow {\bf R}\times {\bf R} \rightarrow {\bf R} \rightarrow {\bf R}. $$ These tell the whole story; cycles appear and disappear and the homology groups change accordingly.

Dimension $1$ homology groups: $$0\rightarrow 0 \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow {\bf R} \rightarrow 0. $$ These don't tell the whole story; it is impossible to deduce from this sequence that one cycle appeared and another disappeared at the same time!

Now, we are trying to capture the cycles that

• are born, as cycles, in complex $K^{i}$, and
• are killed, as boundaries, in complex $K^{i+p}$.

Definition. Given a positive integer $p$, the $p$-persistence $k$th homology group of $\{K^{i}\}$ is $$H_{k}^{i,p}(K^{i})=Z_{k}^{i}/(B_{k}^{i+p}∩Z_{k}^{i}),$$ where

• $Z_{k}^{i}$ is the $k$-cycle group of $K^{i}$ and
• $B_{k}^{i}$ is the $k$-boundary group of $K^{i}$.

Persistence is a fruitful idea because we are able to handle ambiguity of data in a purely topological way.