This site is being phased out.
Diffusion equation
Contents
The PDE of diffusion
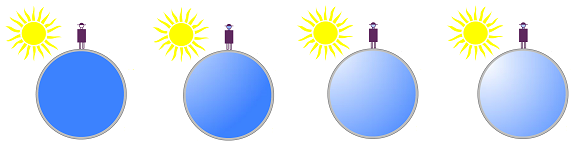
Just as advection, heat transfer exhibits a dispersal pattern. We can see, however, that without a flow to carry material around, the pattern doesn't have a particular direction:
Instead of being carried around, the heat is exchanged -- with adjacent locations. It's a circle.
The process is also known as diffusion.
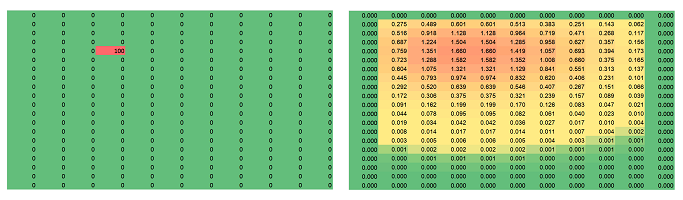
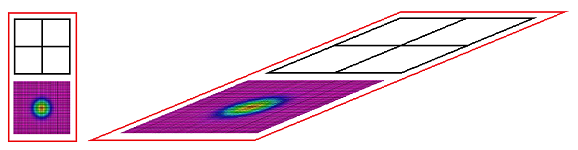
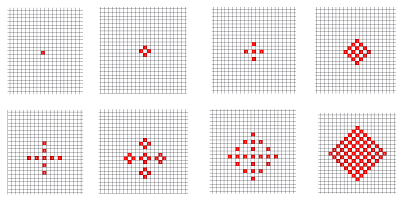
To model heat propagation, imagine a grid of square rooms and the temperature of each room changes by a proportion of the average of the temperature of the four adjacent rooms. Its spreadsheet simulation is given by the following short formula: $$\texttt{RC = RC - .25*h*( (RC-RC[-1]) + (RC-RC[1]) + (RC-R[-1]C) + (RC-R[1]C) )}$$ Only a proportion $h$, dependent on the presumed length of the time interval, of the total amount is exchanged. The two images below are the initial state (a single initial hot spot) and the results (after $1,700$ iterations) of such a simulation for $h=.01$ and the temperature at the border fixed at $0$:
On a larger scale, the simulation produces a realistic circular pattern:
A more careful look reveals that to model heat transfer, we need to separately record the exchange of heat with each of the adjacent rooms.
The process we are to study obeys the following law of physics.
Newton's Law of Cooling: The rate of cooling of an object is proportional to the difference between its temperature and the ambient temperature.
This law is nothing but a version of the ODE of population growth and decay -- with respect to the exterior derivative $d_t$ over time. For each cell there are four adjacent cells and four temperature differences, $d_x$, to be taken into account. The result is a partial differential equation (PDE).
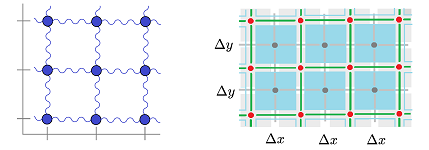
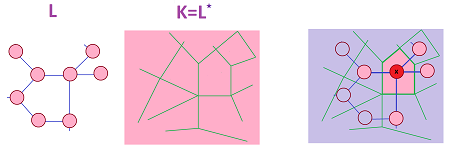
Below, we derive a PDE of forms for the diffusion process. The setup is as follows. A certain material is contained in a grid of rooms and each room (an $n$-cell) exchanges the material with its neighbors through its walls ($(n-1)$-cells). We will assume initially that the space is the standard cubical complex ${\mathbb R}^n$ and the time is the standard complex ${\mathbb R}$. For now, we ignore the geometry of time and space.
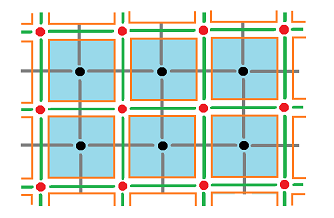
Dually, one can think of pipes ($1$-cells) connecting compartments or ponds ($0$-cells) in the centers of the rooms each of which exchanges the material with its neighbors. We will use both of the two approaches.
Below, the rooms are blue, the walls are green, and the pipes are gray:
We assume that the time increment is long enough
- for the material in each room to spread uniformly; or
- for the material to pass from one end of the pipe to the other.
What makes this different from ODEs is that the forms will have two degrees -- with respect to location $x$ and with respect to time $t$.
The amount of material $U=U(\alpha,t)$ is simply a number assigned to each room $\alpha$ which makes it an $n$-form. It also depends on time which makes it a $0$-form. We call it an $(n,0)$-form, an $n$-form with respect to location and a $0$-form with respect to time.
Definition. In the product of two cubical complexes $K\times L$, an differential $(k,m)$-form is a real-valued linear operator defined on cells $a\times b$, where $a$ is a $k$-cell in $K$ and $b$ is an $m$-cell in $L$.
The outflow gives the amount of flow across an $(n-1)$-face (from the room to its neighbor) per unit of time. It is also a number assigned to each “pipe” $p$ that goes through each wall from one cell to the next. So, $F=F(p,t)$ is a dual $(n-1,0)$-form.
Notation:
- $d_t$ is the exterior derivative with respect to time (simply the difference in ${\mathbb R}$); and
- $d_x$ is the exterior derivative with respect to location. $\\$
Below, we routinely suppress $t$ for the second variable.
The “conservation of matter” in cell $\alpha$ gives us the following. The change of the amount of the material in room $\alpha$ over the increment of time is equal to $$d_t U(\alpha)=-\bigg( \text{ sum of the outflow } F \text{ across the walls of } \alpha\bigg).$$ Naturally, the walls form the boundary $\partial \alpha$ of $\alpha$. Therefore, we have $$d_t U(\alpha)= -F^\star(\partial \alpha)$$ or, by the Stokes Theorem, $$d_t U(\alpha) = -(d_x F^\star)(\alpha).$$
Now, we need to express $F$ in terms of $U$. The flow $F(a^\star)=F^\star(a)$ through wall $a$ of room $\alpha$ is proportional to the difference of the amounts of material (or, more precisely, the density) in $\alpha$ and the other room adjacent to $a$. So, $$F^\star(a) = - k(a)d_x(\star U)(a^\star).$$ Here, $k(a) \ge 0$ represents the permeability of the wall $a$ at a given time. Since $a$ is an $(n-1)$-cell, $k$ is an $(n-1)$-form with respect to space. It is also a $0$-form with respect to time.
The result of the substitution is a PDE of second degree called the diffusion equation of forms: $$\begin{array}{|c|} \hline \\ \quad d_t U = d_x \star kd_x \star U \quad \\ \\ \hline \end{array}$$
The right-hand side is seen in the Hodge duality diagram below. We start with $U$ in the right upper corner and make the full circle: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccl} C ^{n-1}(K)\ & \ra{d_x} & C ^n(K) & \ni U \\ \da{\star}\ua{} & \ne & \da{\star}\ua{} \\ C ^1(K^\star)& \la{d_x} & C ^0(K^\star)\\ \end{array} $$ The multiplication by $k$ is implied.
In general, $k$ cannot be factored out. Unless of course $k$ happens to be constant with respect to space; then the right-hand side is $kU' '$.
This was an outline. In the following, we develop both the mathematics and the simulations for progressively more complex settings.
Simulating diffusion with a spreadsheet
For the simplest spreadsheet simulation we previously considered dimension $1$: the material is contained in a row of rooms and each room exchanges the material with its two neighbors through its walls.
Next, dimension $2$.
The amount of material $U=U(\tau,t)$ is a $2$-form with respect to location and a $0$-form with respect to time.
The outflow gives the amount of flow across a $1$-face (from the room to its neighbor) per unit of time. It is simply a number assigned to each “pipe” $p$ that goes through each wall from one cell to the next. So, $F=F(p,t)$ is a $(1,1)$-form, but over the dual grid.
The “conservation of matter” for cell $\tau$ implies that the change of the amount of the material over the increment of time $d_t U(\tau)$ is, as before, the negative sum of the outflow $F( \cdot )$ across the four walls of $\tau$: $a,b,c,d$. Let's rewrite the latter: $$=-\Big( F^\star(a)+F^\star(b)+F^\star(c)+F^\star(d)\Big) =- F^\star(a+b+c+d).$$
Now, we need to express $F$ in terms of $U$. The flow $F(a^\star)=F^\star(a)$ through face $a$ of cell $\tau$ is proportional to the difference of the amounts of material in $\tau$ and the other $2$-cell adjacent to $a$. So, $$F^\star(a) = - kd_x(\star U)(a^\star).$$
Exercise. Demonstrate how the above analysis leads to the “naive” spreadsheet simulation presented in the beginning of the section.
Note: One needs to use a buffer (an extra sheet); otherwise Excel's sequential -- cell-by-cell in each row and then row-by-row -- manner of evaluation will cause a skewed pattern:
A simulation of heat transfer from a single cell is shown below:
Link to file: Spreadsheets.
Exercise. (a) What kind of medium would create an oval diffusion pattern? Demonstrate. (b) What about an oval not aligned with the axes?
Exercise. Modify the formula to create a simulation for diffusion on the torus.
Next we consider diffusion on metric complexes.
We have used interchangeably “amount of material” and “density of material”. The reason is that we ignore the possibility of cells of different sizes (and shapes) by assuming the simplest geometry.
We have modeled heat transfer with this formula: $$\texttt{RC = RC - k*( (RC-RC[-1]) + (RC-RC[1]) + (RC-R[-1]C) + (RC-R[1]C) )}$$
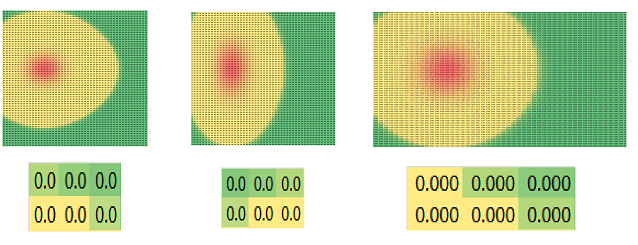
What if the horizontal walls are longer than the vertical ones? Then more heat should be exchanged across the vertical walls than the horizontal ones.
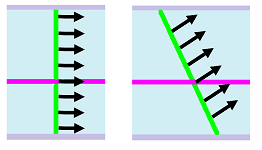
We can change the coefficients of “vertical” differences in the above formula to reflect that: $$\texttt{RC = RC - k*( .5*(RC-RC[-1]) + .5*(RC-RC[1]) + 2*(RC-R[-1]C) + 2*(RC-R[1]C) )}$$ We can see how the material travel farther -- as measured by the number of cells -- in the vertical direction (second image) than normal (first image):
Yet, if we stretch -- justifiably -- the cells in the spreadsheet horizontally (third image), the pattern becomes circular again!
In summary, the amount of heat exchanged between two rooms is proportional to:
- the temperature difference,
- the permeability of the wall (dually: the conductance of the pipe),
- the area of the wall that separates them (dually: the cross section of the pipe), and
- inversely, to the distance between the centers of mass of the rooms (dually: the length of the pipe).
Let's split the data into three categories:
- the adjacency of rooms (and the pipes) is the topology,
- the areas of the walls (and the lengths of the pipes) is the geometry, and
- the properties of the material of the walls (and the pipes) is the physics. $\\$
They are given by, respectively:
- the cell complex $K$,
- the Hodge star operator $\star^m :C^m(K)\to C^{n-m}(K^\star)$, and
- the $(n-1)$-form $k$ over $K$.
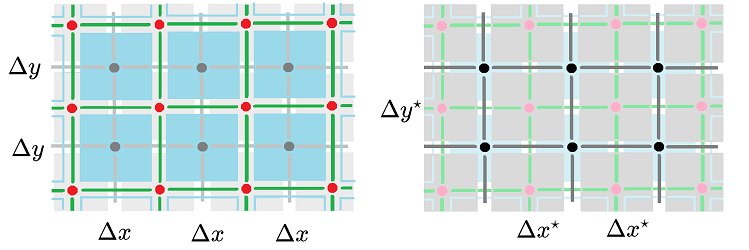
Suppose the geometry of space is supplied by means of the $m$-dimensional volume $|b|$ of each $m$-cell $b$ -- in both primal and dual complexes $K$ and $K^\star$. Now, the $m$th Hodge star is a diagonal matrix whose entries are the ratios of dual and primal volumes (up to a sign) in each dimension $m=0,1, ...,n$: $$\star ^m_{ii}=\pm\frac{|a_i^\star|}{|a_i|}.$$
Similarly the geometry of time is supplied by means of the length $|t|$ of each time interval ($1$-cell) $t$ -- in both primal and dual complexes ${\mathbb R}$ and ${\mathbb R}^\star$. The Hodge star is a diagonal matrix whose entries are the reciprocals of the lengths of these intervals: $$\star ^1_{ii}=\pm\frac{1}{|t_i|}.$$
Recall that the right-hand side of our equation is the familiar second derivative (with respect to space) of an $n$-form with an extra factor $k$: $$(kU_x)_x:=(kU')' = d_x \star kd_x \star U.$$ As before, this expression is seen in the Hodge duality diagram, with the factors that come from the star operators also shown: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} &\quad C ^{n-1}(K) & \ra{\quad d_x \quad} & C ^n (K) & \ni U \\ &\quad\quad\quad\quad\quad\ua{\times\frac{|a^{n-1}|k(a^{n-1})}{|b^1|}} & \ne & \quad\da{\times\frac{|b^0|}{|a^n|}} \\ &\quad C ^1(K^\star)& \la{\quad d_x \quad} & C ^0(K^\star),\\ \end{array} $$ where $a^m$ is a primal $m$-cell and $b^m$ is a dual $m$-cell.
If we are to use the derivative, instead of the exterior derivative, with respect to time, we need to consider two issues. First, let's recall that when studying ODEs we used the function $q:C_1({\mathbb R})\to C_0({\mathbb R})$ given by $$q\Big([i,i+1] \Big)=i,$$ to make the degrees of the forms, with respect to time, match. Second, in addition to the above list, the amount of material exchanged between two rooms is also proportional to the length of the current time interval $|t|$. Then our PDE takes the form: $$d_tUq^{-1}=(kU_x)_x|t|,$$ with both sides $(n,0)$-forms. Consider the first derivative with respect to time: $$U_{t}:=U'=\star d_t U=\tfrac{1}{|t|}d_tU.$$
Definition. Given a metric complex $K$ of dimension $n$, the diffusion equation is: $$U_t q^{-1}= (kU_x)_x,$$ where $U$ is an $(n,0)$-form over $K\times {\mathbb R}$.
The abbreviated version is below. $$\begin{array}{|c|} \hline \\ \quad U_t = (kU_x)_x \quad \\ \\ \hline \end{array}$$
Definition. An initial value problem (IVP) for diffusion is a combination of the diffusion equation and an initial condition (IC): $$U_t = (kU_x)_x,\ U(\cdot,A_0)=u_0\in C^n(K).$$ Then a $(n,0)$-form $U$ on $K\times {\mathbb R} \cap \{A\ge A_0\}$ that satisfies both conditions is called a (forward) solution of the IVP.
Because the exterior derivative with respect to time is simply the difference of values, a solution is easy to construct iteratively.
Theorem (Existence and Uniqueness). The solution to the IVP above exists and is given by $$U(\cdot,A_0):=u_0,\quad U(\cdot,A+1):=U(\cdot,A)+(kU_x)_x(\cdot ,A)|[A,A+1]|,\ \forall A\ge A_0,$$ provided $\tfrac{1}{|a|}\in R$ for every cell $a$ in $K\sqcup K^\star$.
Exercise. Provide a weaker sufficient condition for existence.
Note: Boundary values problems lie outside the scope of this book.
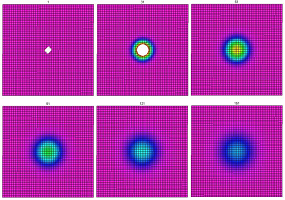
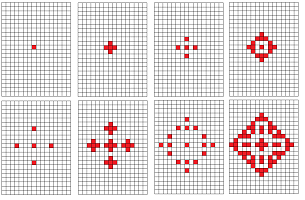
Example. The choice of $$K={\mathbb R}^2,\quad R={\bf Z}_2,$$ produces this simple “cellular automaton”:
$\square$
Exercise. Derive the dual diffusion equation: “Suppose the material is located in the nodes of a graph in ${\bf R}^n$ and the amount of material is represented by a $0$-form $V$...”
Note: One can allow the physics to be absorbed into the geometry. As the transfer across a primal $(n-1)$-cell $a$ is proportional to its permeability $k(a)$, we can simply replace the volume $|a|$ of $a$ with $k(a)|a|$, provided $k\ne 0$. Then the right-hand side of our equation becomes the Laplacian (with respect to space) $U_{xx}=\Delta U$.
We test the performance of this equation next.
How diffusion patterns depend on the sizes of cells
Let's consider diffusion over a $1$-dimensional metric cubical subcomplex of ${\mathbb R}$.
The diagonal elements of the Hodge star operator for dimension $n=1$ are: $$\star ^1_{ii}=\frac{|\text{point}|}{|\text{edge}|} = \frac{1}{\text{length}} = \frac{1}{|a_i|}.$$ Then $\star ^1$ and $\star ^0$ give us our Hodge duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^0(K) & \ra{d} & C ^1(K) & \ni U \\ & \ua{\times\frac{|b|}{1}} & \ne & \da{\times\frac{1}{|a|}} \\ & C ^1(K^\star)\ & \la{d} & C ^0(K^\star),\\ \end{array} $$ where $a,b$ are primal and dual $1$-cells respectively. The right-hand side of our equation will have extra coefficients: the lengths of the cells appear twice as we make a full circle.
First, it's the length of the cell itself, $\tfrac{1}{|a|}.$ Then the equation will contain: $$\frac{U(a)}{|a|}.$$ That's the density of the material inside $a$.
Second, it's the lengths of the $1$-cells dual to the endpoints of $a=AB$: $$\frac{1}{|A^\star|},\frac{1}{|B^\star|}.$$ The denominators are the lengths of the pipes.
Conclusion: The amount of material exchanged by a primal $1$-cell $a$ with its neighbor $a'$ is
- directly proportional to the difference of density in $a$ and $a'$, and
- inversely proportional to the length of the pipe that leaves $a$ for $a'$.
We confirmed these ideas with a spreadsheet simulation in chapter 1 for dimension $1$.
For dimension $n=2$, we know the diagonal entries in the case of a rectangular grid ${\mathbb R}^2$: $$\star ^2_{ii} = \frac{1}{\text{area}}, \quad \star ^1_{ii} = \frac{\text{length}}{\text{length}}. $$ Then $\star ^2$ and $\star ^1$ give us our Hodge duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} & C ^1(K) & \ra{d} & C ^{2}(K) & \ni U \\ & \ua{\times\frac{|b|}{|a|}} & \ne & \da{\times\frac{1}{|\sigma|}} \\ & C ^1(K^\star)\ & \la{d} & C ^0(K^\star),\\ \end{array} $$ where $a,b$ are primal and dual $1$-cells respectively and $\sigma$ is a $2$-cell.
Just as above, we notice that $U(\sigma)/|\sigma|$ is the density inside $\sigma$. The second coefficient $|a|/|a^\star|$ is new. We see here the $1$-cell that represents the wall and its dual that represents the pipe: $$\frac{\text{length of the wall}}{\text{length of the pipe}}.$$
Conclusion: The amount of material exchanged by a primal $2$-cell $\sigma$ with its neighbor $\tau$ is
- directly proportional to the difference of density in $\sigma$ and that of $\tau$,
- inversely proportional to the length of the pipe from $\sigma$ to $\tau$, and
- directly proportional to the length of the wall (thickness of this pipe).
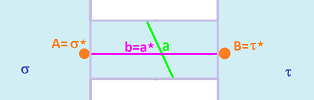
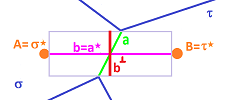
If we use the $2\times 1$ grid, we have the following lengths of $1$-cells:
- horizontal primal: $|a|=2$, dual: $|a^\star|=1$;
- vertical primal: $|a|=1$, dual: $|a^\star|=2$. $\\$
Then the Excel formula is the same as the one discussed above: $$\texttt{RC = RC - .0025*( .5*(RC-RC[-1]) + .5*(RC-RC[1]) + 2*(RC-R[-1]C) + 2*(RC-R[1]C) )}$$ This formula, with a single source, produces a circular pattern on a spreadsheet with appropriately sized cells, as expected:
Exercise. Show that with the horizontal walls impenetrable, the transfer pattern will be identical to the $1$-dimensional pattern.
To summarize, the material flows from room $\sigma$ to room $\tau$ through what appears to be a pipe of length $|a^\star|$ and width $|a|$:
How diffusion patterns depend on the angles between cells
What if the wall between two rooms is slanted? Does it affect the amount of liquid that crosses to the other room?
If two walls are made of the same material (and of the same thickness), the slanted one will allow less liquid to flow through the pipe. In fact, what matters is the normal component of the flow across the wall.
We arrive to the same idea if, dually, we expand our pipe, $a^\star$, to the largest possible width, $|a|$:
Then $a$ is a (possibly non-orthogonal) cross-section of pipe $a^\star$.
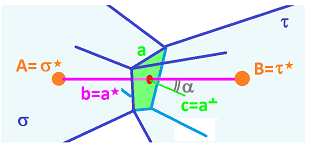
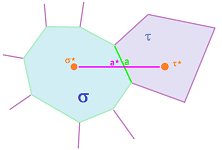
Now, to make this more precise, consider the general case of an $n$-dimensional room, $\sigma$, with an $(n-1)$-dimensional wall, $a$, and still a $1$-dimensional pipe, $a^\star$. It is illustrated below for $n=3$:
As before, we are looking at the angle $\alpha$ between the normal $c=a^\perp$ of the wall $a$ and the pipe $a^\star$. Then
- the normal component of the flow is acquired by multiplying by the cosine of the angle between $a$ and $a^\star$.
Conclusion: The amount of material exchanged by a primal $n$-cell $\sigma$ with its neighbor $\tau$ is
- directly proportional to the difference of density in $\sigma$ and that of $\tau$; i.e., $U(\sigma)/|\sigma| - U(\tau)/|\tau|,$
- inversely proportional to the length $|a^\star|$ of the pipe $a^\star$ that leaves $\sigma$ for $\tau$,
- directly proportional to the area $|a|$ of the wall $a$, and
- directly proportional to the cosine of the angle between this pipe and this wall, $\cos \widehat{aa^\star}$.
Next, the iterative formula.
The boundary -- as a chain -- of a cell is the sum of its boundary cells taken with appropriate orientations: $$\partial \sigma=\displaystyle\sum_{a\in \partial \sigma} \pm a.$$
Therefore, the net change of material in cell $\sigma$ is the sum of the amounts exchanged through its boundary cells: $$U(\sigma,t+1)-U(\sigma,t)= \displaystyle\sum_{\partial \sigma} \tfrac{|a|}{|a^\star|}\cos \widehat{aa^\star} \Big[ \tfrac{U(\sigma)}{|\sigma|} - \tfrac{U(\tau_a)}{|\tau_a|} \Big],$$ where $$\tau_a:=\sigma+(\partial a^\star)^\star$$ is the $n$-cell that shares wall $a$ with $\sigma$.
It is easy to confirm that the right-hand side is nothing but the same expression $\star d \star d U$ as before. What has changed is the coefficients of the matrix of the Hodge star operator of the new geometry of the complex: $$\star^k_{ii}=\tfrac{|a_i|}{|a_i^\star|}\cos \widehat{a_ia_i^\star},$$ where $a_i$ is the $i$th $k$-cell. Recall that the feature of a non-rectangular geometry is that the angles $\cos\widehat{aa^\star}\ne 1$.
Exercise. Create a spreadsheet for the above formula and confirm the results presented below.
With this formula, we are able to study diffusion or heat transfer through an anisotropic or even irregular pattern, such as fabric, plant cells, or sunflower seeds:
Example (trapezoid grid). Consider this trapezoid grid:
It is made from a square grid by turning the vertical edges by the same angle alternating left and right. According to our analysis, the horizontal flow will be slower than before, but what about vertical? $\square$
Exercise. (a) Compare the speed of the horizontal flow and the vertical to those of the original grid. (b) Verify the conclusion with a simulation.
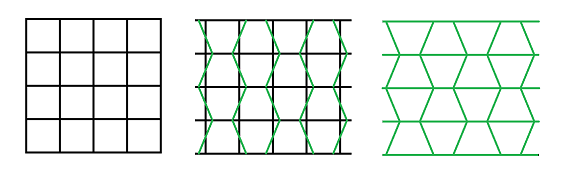
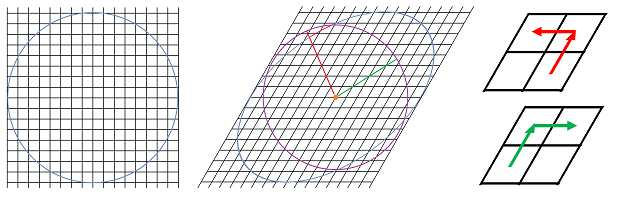
Example (rhomboid grid). Consider now the rhomboid grid:
The pattern isn't circular anymore! And it not aligned with the directions of the walls:
This is how this pattern is acquired. Even with slanted walls, the exchange with each of the four adjacent cells remains identical. That's why the result of the spreadsheet simulation is still circular (left):
The pattern is shown circular, however, only because the spreadsheet displays the shapes of the cells as squares. To see the true pattern, we have to skew the image (right) in such a way that the squares become rhombi.
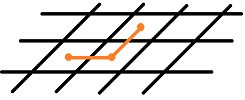
The outcome may seem unexpected because the physics appears to be symmetric. It is true that the pattern of the flow is identical for the two directions along the grid, and therefore, the speed of propagation in either of the two directions is the same, just as before. Still, what about the other directions? Below, the red and green segments are equal in length, but to follow the red one, we would have to cross more walls than for the green:
We conclude that the skewed pattern is caused by the “anisotropic” nature of the medium. $\square$
Exercise. (a) Verify these conclusions with a simulation. (b) What are the directions of the fastest and the slowest propagation? Explain.
Exercise. To study a triangular grid, one needs a non-cubical cell complex. Use a spreadsheet to model diffusion on a triangular grid produced by diagonally cutting the squares.
Exercise. Add a flow to the diffusion (resulting in a “convection–diffusion equation”).
Reaction–diffusion systems
This model corresponds to the change in space and time of the concentration of two chemical substances: local chemical reactions in which the substances are transformed into each other is combined with diffusion which causes the substances to spread out over a surface in space. Either of the two functions, $u,v$, in a reaction diffusion system represents a concentration variable.
This is the general two-component system: $$\begin{align} \partial_t u &= q_u \,\Delta u + F(u,v), \\ \partial_t v &= q_v \,\Delta v + G(u,v). \end{align}$$
We consider an activator-inhibitor system: the first component stimulates the production of both components while the second inhibits their growth: $$\begin{align} F(u,v)=f(u)-av, \\ G(u,v)=g(u)-bv. \end{align}$$ Also, $q_u,q_v>0$.
The PDE of wave propagation
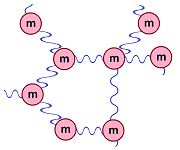
We next return to the wave equation and consider an array of objects connected by springs, both vertical and horizontal:
Just as before, we will provide the mathematics to describe the following three parts of the setup:
- the topology of the cell complex $L$ of the objects and springs,
- the geometry given to that complex such as the lengths of the springs, and
- the physics represented by the parameters of the system such as those of the objects and springs.
Let $u(t,x)$ be the function that measures the displacement from the equilibrium of the object associated with position $x$ at time $t$ (we will suppress $t$). It is an algebraic quantity: $$u=u(t,x)\in R \times R.$$ As such, it can represent quantities of any nature that may have nothing to do with a system of objects and springs; it could be a wave in a liquid:
Here, the particles of the liquid are vertically displaced while waves propagate horizontally (or we can see the pressure or stress vary in a solid medium producing sound).
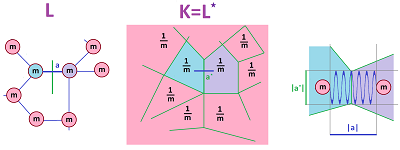
First, we consider the spatial variable, $x\in {\bf Z}\times {\bf Z}$. We think of the array -- at rest -- as the standard $2$-dimensional cubical complex $L={\mathbb R}^2$. The complex may be given a geometry: each object has a (possibly variable) distances $\Delta x, \Delta y$ to its neighbors and the distances between the centers of the squares have length $\Delta x^\star, \Delta y^\star$, etc. We think of $u$ as a form of degree $0$ -- with respect to $x,y$.
According to Hooke's law, the force exerted by the spring is $$F_{Hooke} = -k df,$$ where $df\in R$ is the displacement of the end of the spring from its equilibrium state and the constant, stiffness, $k\in R$ reflects the physical properties of the spring. If this is the spring that connects locations $x$ and $x+1$, its displacement is the difference of the displacements of the two objects.
The forces exerted on the object at location $x$ are the four forces of the four springs attached to it: $$\begin{array}{llll} H & = H_{x,x-1} + H_{x,x+1} + H_{y,y-1} + H_{y,y+1}\\ & = k[ u(x-1,y) - u(x,y) ] \\ & + k[ u(x+1,y) - u(x,y) ] \\ & + k[ u(x,y-1) - u(x,y) ] \\ & + k[ u(x,y+1) - u(x,y) ] . \end{array}$$
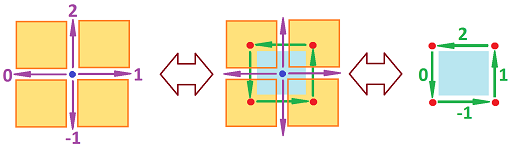
We still consider only $0$- and $1$-forms but on the standard $2$-dimensional cubical complex $L={\mathbb R}^2$. Hodge duality is slightly more complicated here. As an example, these are a $1$-form $\varphi$ and its dual $1$-form $\varphi^*$:
Just as in the $1$-dimensional case, each bracketed term in the expression for $F$ is the exterior derivative: two with respect to $x$ and two with respect to $y$: $$\begin{array}{llll} k[ u(x-1,y) - u(x,y) ] &= kd_xu([x,x-1],y), \\ k[ u(x+1,y) - u(x,y) ] &= kd_xu([x,x+1],y), \\ k[ u(x,y-1) - u(x,y) ] &= kd_yu(x,[y,y-1]),\\ k[ u(x,y+1) - u(x,y) ] &= kd_yu(x,[y,y+1]). \end{array}$$ We can rearrange these terms as they all start from $(x,y)$: $$H= kdu\left\{\begin{array}{llll} & & +\{x\}\times [y,y+1] \\ &+[x,x-1]\times \{y\} & & +[x,x+1]\times \{y\}\\ & & +\{x\}\times [y,y-1] \end{array}\right\},$$ where $d=(d_x,d_y)$. To get the duals of these edges, we just rotate them counterclockwise. Then, $$H= kd^\star u\left\{\begin{array}{llll} & & +[x^+,x^-]\times \{y^+\} \\ &+\{x^-\}\times[y^+,y^-] & & +\{x^+\}\times[y^-,y^+]\\ & & +[x^-,x^+]\times \{y^-\} \end{array}\right\},$$ where “$^\pm$” stands for “$\pm 1/2$”.
Observe that the dual edges are aligned counterclockwise along the boundary of the square neighborhood $[x^-,x^+]\times [y^-,y^+]$ of the point $(x,y)$. That neighborhood is the Hodge dual of this point. We recognize this expression as a line integral: $$H= \displaystyle\int_{\partial (\star (x,y))} \star kdu.$$
Now by the Stokes Theorem, the integral is equal to: $$H= \star d_x \star kd_xu .$$ Since the left-hand side is the same as before, we have the same wave equation: $$m u_{tt} = (k^\star u_x)_x.$$
Note that for a constant $k$, we are dealing with the second derivative of the $0$-form $u$ with respect to space:
$$u' '=\star d_x\star d_xu = \Delta u.$$
Compare it to the second derivative of a $1$-form $U$ with respect to space:
$$U' '=d_x\star d_x\star U = \Delta U,$$
which we used to model $1$-dimensional diffusion. The difference is seen in the two different starting points in the same Hodge duality diagram:
$$
\newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!}
\newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.}
\newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!}
\newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.}
%
\begin{array}{ccccccccccc}
u\in & C ^0({\mathbb R}^2) \ & \ra{d_x} & C ^1({\mathbb R}^2) &\ni U \\
& \ua{\star} & \ne & \da{\star} \\
& C ^1(({\mathbb R}^2)^\star) \ & \la{d_x} & C ^0(({\mathbb R}^2)^\star)\\
\end{array}
$$
Then,
$$d_xu' ' = (d_xu)' '.$$
Second, we consider the temporal variable, $t\in {\bf Z}$. We think of time as the standard $1$-dimensional cubical complex ${\mathbb R}_t$. The complex is also given a geometry. It is natural to assume that the geometry has no curvature, but each increment of time may have a different duration (and, possibly, $\Delta t \ne \Delta t^\star$). We think of $u$ as a form of degree $0$ with respect to $t$.
Now suppose that each object has mass $m$. Then, by the Second Newton's Law, the total force is $$F=m \cdot a,$$ where $a$ is the acceleration. It is the second derivative with respect to time, i.e., this $0$-form: $$a=u_{tt}:=\star d_t \star d_t u . $$ The mass $m$ is a $0$-form too and so is $F$. Note that the stiffness $k$ is also a $0$-form with respect to time.
Now, with these two forces being equal, we have derived the wave equation of differential forms: $$\begin{array}{|c|} \hline \\ \quad m u_{tt} = (k^\star u_x)_x. \quad \\ \\ \hline \end{array}$$
If $k$ and $m$ are constant forms (and $R$ is a field), the wave equation takes a familiar shape: $$u_{tt}=\tfrac{k}{m}u_{xx}.$$
Exercise. Derive the dual (with respect to space) wave PDE.
Next we simulate wave propagation with a spreadsheet. The $2$-dimensional case is treated with the formula given above. This is the result of a circular wave with a single source bouncing off the walls of a square box.
Exercise. Implement the wave illustrated on the first page of this chapter.
Example. The choice of $$K={\mathbb R}^2,\quad R={\bf Z}_2,$$ produces this simple “cellular automaton”:
$\square$
Other complexes
In general, the medium may be non-uniform and anisotropic, such as wood:
We model the medium with a graph of springs and objects with a possibly non-trivial geometry:
We are now in the same place as with the diffusion equation. We split the data into three categories:
- 1. the adjacency of the springs (and the objects) is the topology,
- 2. the lengths of the springs (and the angles and the areas of their cross-sections) is the geometry, and
- 3. the Hooke's constants of the springs is the physics. $\\$
They are given by, respectively:
- 1. the cell complex $L$,
- 2. the Hodge star operator $\star^m :C^m(L)\to C^{n-m}(L^\star)$, and
- 3. the primal $1$-form $k\in C^1(L)$.
The two complexes dual to each other are shown below:
The total force that affects the object located at vertex $x$ in $L$ is $$F= \star \displaystyle\int_{\partial (\star x)} \star kdu.$$ Therefore, we end up with the same wave equation as above. Its right-hand side is seen as the full circle in the Hodge duality diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} u\in & C ^0(L) & \ra{\quad d_x \quad} & C ^1(L) & \\ &\quad\quad \quad\ua{\times\frac{|a^0|}{|b^n|}} & \ne & \quad\da{\times\frac{|b^{n-1}|}{|a^1|}} \\ & C ^n(L^\star)& \la{\quad d_x \quad} & C ^{n-1}(L^\star),\\ \end{array} $$ where $a$ and $b$ are dual.
The geometry of the primal complex $L$ is given first by the lengths of the springs. What geometry should we give to the dual complex $K=L^\star$?
First, the meaning of the coefficients of the Hodge star operator are revealed to be represented by the stiffness $k(a)$ of spring $a$. In fact, it is known to be directly proportional to its cross-sectional area $|b|$ and inversely proportional to its length $|a|$: $$k(a):=E\frac {|b|} {|a|},$$ where $E$ is the “elastic modulus” of the spring. Plainly, when the angles are right, we have simply $b=a^\star$.
Second, we assign the reciprocals of the masses to be the $n$-volumes of the dual $n$-cells: $$|x^\star|:=\frac{1}{m(x)}.$$
Then we have the simplified -- with the physics taken care of by the geometry -- wave equation, $$u_{tt}=(E^\star u_{x})_x,$$ where $E$ is the $1$-form of elasticity. Its right-hand side is seen as the full circle in the Hodge duality diagram modified accordingly: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} \newcommand{\la}[1]{\!\!\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\ua}[1]{\left\uparrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccccccc} u\in & C ^0(L) & \ra{\quad d_x \quad} & C ^{1}(L) & \\ &\quad\quad \quad\ua{\times\frac{1}{m(b^n)}} & \ne & \quad\da{\times k(a^1)} \\ & C ^n(L^\star)& \la{\quad d_x \quad} & C ^{n-1}(L^\star)\\ \end{array} $$