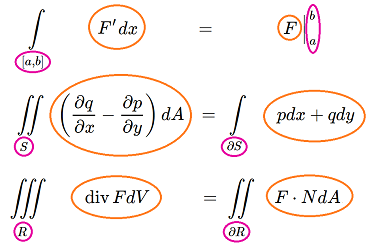This site is being phased out.
Why do we need differential forms?
Redirect page
Redirect to:
We would like to develop a modern version of vector calculus based on differential forms. Do we really need this more advanced approach?
Contents
Problem 1: What if the dimension is n?
There are many integral theorems of vector calculus. In fact, one for each dimension, which may just be too many...
Let's go down from dimension $3$ and see what they have in common.
Green's Theorem: $$\int\int_{S} \left( \frac{\partial q}{\partial x} - \frac{\partial p}{\partial y} \right) dA = \int_{\partial S} p dx + q dy, $$ where $\partial S$ stands for the boundary of $S$.
In this case, the integrands are: $$\left( \frac{\partial q}{\partial x} - \frac{\partial p}{\partial y} \right) dA \text{ and }p dx + q dy.$$ And the domains of integration are a solid and its boundary surface:
Gauss' Theorem: $$\int\int\int_{R} {\rm div} F dV = \int\int_{\partial R} F \cdot N dA.$$
In this case, the integrands are $${\rm div} F dV \text{ and } F \cdot N dA.$$ And the domains of integration are a plane region and its boundary curve:
again.
Fundamental Theorem of Calculus: $$\int_{[a,b]} F' dx = F |_{a}^b.$$
If we think of the right-hand side as an integral too, the integrands are $$F' dx \text{ and } F.$$ And the domains of integration are a segment and its boundary points:
again!
What do these three have in common?
Even though there seems to be no connected between the integrands, the pattern of the domains of integration is clear.
What's right on the surface is that the relation between the domains of integration on the left and on the right is the same in all these formulas:
That's a start!
Now, there must be some kind of a relation for the integrands too. The Fundamental Theorem of Calculus suggests that this relation may be something like this:
Of course for the other theorems this relation doesn't work. To make sense of this idea we treat those integrands as a special kind of functions called "differential forms".
What is the point of this "innovation"? With this approach we have just one general theorem that includes them all, and much more...
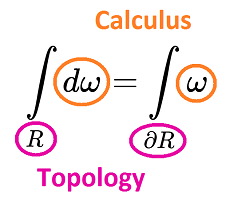
Stokes Theorem: $$\int_R d \omega = \int_{\partial R} \omega.$$
Here $d \omega$ stand for the exterior derivative of differential form $\omega$.
Note: The relation between $R$ and $\partial R$ is an issue of topology. The relation between $d \omega$ and $\omega$ is an issue of calculus, calculus of differential forms.
Stokes theorem deconstructed:
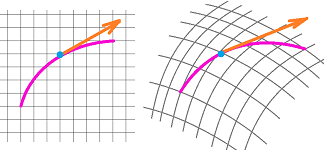
Problem 2: What if the space is curved?
It is, according to Einstein. Indeed, we know that light curves.
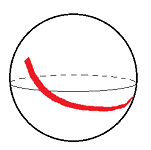
A simpler, more tangible, task would be to develop calculus for the sphere: curve length, surface area, etc.
In either case, the curvature of the underlying "manifold" has to be taken into account.
Compare the motion of an object in the two setups:
- the Cartesian, flat space: motion through the plane ${\bf R}^2$ (or space ${\bf R}^3$, etc); or
- the Riemanian, curved space: motion on the surface of the sphere (or the $n$-sphere ${\bf S}^n$), etc.
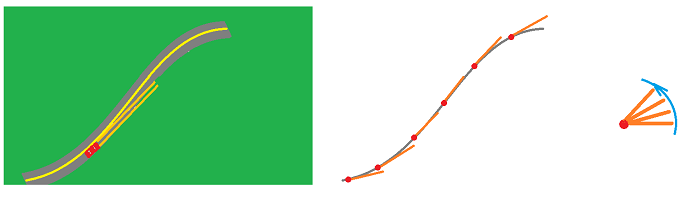
In either case the motion is described by a parametric curve $r=r(t)$. However, what about the velocity? It is supposed to be the derivative $r'$ of the curve $r$.
In the former case, it's simple. The velocity vectors live in the same Euclidean plane ${\bf R}^2$ as the motion itself.
But in the latter case, the vectors of the velocity don't belong to the original domain anymore! Since they are supposed to point in the direction of the motion, they are vectors tangent to the sphere.
Now, differential forms are special kinds of functions -- functions that are defined on the set of all tangents.
Problem 3: What if the data is discrete?
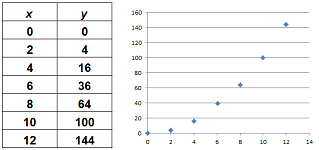
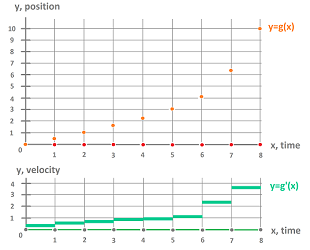
In real-life applications, a function of one variable is simply a series of numbers. Just look at this "graph" of a function in Excel:
How can we do calculus with such functions?
The two main questions are the following.
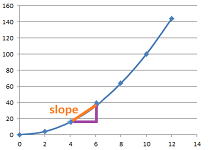
1) What is the function's rate of change?
The derivative tells us the rate of change of data that continuously varies. Its discrete analog is the difference, the difference of values at two consecutive points.
More precisely, if the function is represented as a collection of points, then the "derivative" is the slope of the line that connects a pair of adjacent ones.
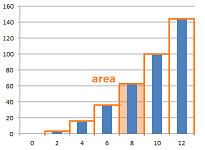
2) What's the area under the graph of the function?
The integral gives us the area under a continuous curve. Its discrete analog is the sum, the sum of the values of the function for all points within the interval.
More precisely, if the function is represented as a collection of rectangles, then the "integral" is the sum of the areas of these rectangles.
With a couple of clicks we can plot the same function with bars instead of dots:
So, the same discrete function has been interpreted in two different ways:
- for differentiation -- as points, and
- for integration -- as rectangles.
This construction leads to the idea of $0$-forms and $1$-forms respectively with latter the derivative of the former:
Of course, when behind the data is a continuous function or process, discretization is a well-established approach. However, discretization means approximation!
Then some theorems (such as the Fundamental Theorem of Calculus) and even some laws of physics (such as conservation of energy) hold only approximately now. This results in error and the propagation of error may result in models that poorly represent the reality.
An easy start
Here's how calculus changes when we start using differential forms.
Suppose $I$ is a closed interval, such as $[a,b]$. Then the (definite) integral of function $f$ over $I$ is understood as $$\int_I \big[ f(x) \big] dx.$$ In other words, the integral is a function with input from integrable functions $f$, like this: $$G[f]=\int_I \big[ f(x) \big] dx.$$ This approach is understandable as the Riemann integral is the limit of the Riemann sums of $f$.
However, it's advantageous to look at this integral as $$\int_I \big[ f(x)dx \big]$$ instead. Here, the integral is a function of $\omega = f(x)dx$. Such an "expression" is called a differential form (of degree 1). The point is that the integral is now a function with input from differential forms $\omega$, like this: $$H[\omega] = \int_I \omega.$$
Even better, it is $\omega$ that is evaluated at $I$: $$\omega[I]=\int_I \omega.$$ This is, in dimension $1$, an indirect definition of differential forms -- they are (linear) functions of intervals.
Now, we just need to figure out what kind of functions behave like this...
Haven't we seen differential forms in calculus? Yes, three examples of forms of degree $1$ follow.
- 1. Differentials:
$$f'(a)=5 \Rightarrow dy=5dx.$$
$$u = x^2 \Rightarrow du = 2xdx.$$
- 3. Separation of variables for solving simple differential equations:
$$\frac{dy}{dx} = \frac{x^2}{y} \Rightarrow ydy = x^2dx.$$
The final point. The connection to topology is very strong. We have already seen the interaction between the region of integration and its boundary in Stokes formula. In fact, differential forms form a "cochain complex" which reveals the topology of the underlying space via cohomology.