This site is being phased out.
Topology in calculus
It's mostly about continuous functions...
Definition. A function $f \colon A \rightarrow {\bf R}$ defined on a subset of ${\bf R}$ is called continuous at $x=a$ in $A$ if $${\rm for \hspace{3pt} any \hspace{3pt}} \epsilon >0 {\rm \hspace{3pt} there \hspace{3pt} is \hspace{3pt} a \hspace{3pt}} \delta >0 {\rm \hspace{3pt} such \hspace{3pt} that \hspace{3pt}} |x - a| < \delta \rightarrow |f(x) - f(a)| < \epsilon.$$
Properties:
- Differentiable $\rightarrow$ continuous (but not vice versa, example $|x|$)
- Graph is one piece (i.e. it is connected)
- If $f, g$ are continuous at $a$ then so are $f+g, f-g, fg$, and $\frac{f}{g}$ (in the last case provided $g(a)≠0$)
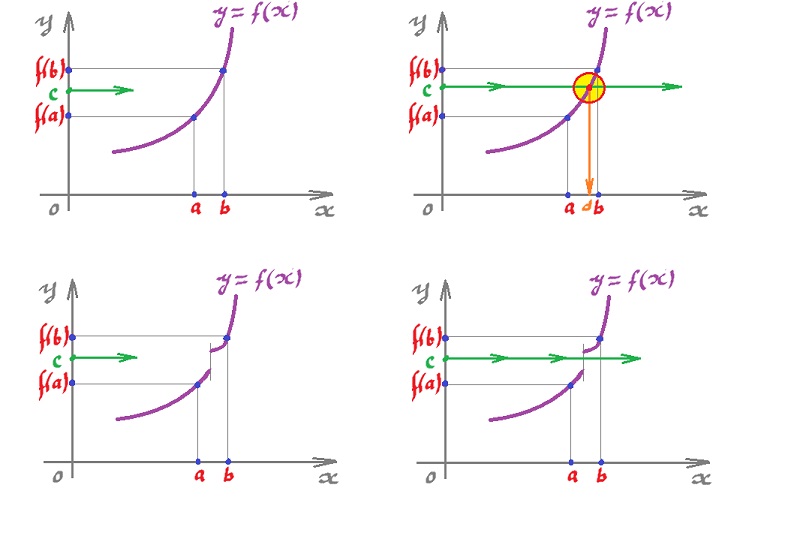
Intermediate Value Theorem. Suppose $f \colon [a, b] \rightarrow {\bf R}$ continuous. Then for any $c$ between $f(a)$ and $f(b)$, there is $d$ in $[a,b]$ such that $f(d) = c$.
Continuous and discontinuous:
The existence of $d$ shows that as the domain $[a,b]$ is connected then so is the image $f([a,b])$.
Exercise. Is it possible that $d$ exists even though $f$ is not continuous? Solution: ![]()
Once we go to higher dimensions $f \colon A \rightarrow {\bf R}^n$, some of the algebraic properties above disappear as there is no multiplication and division any more. You can still add vectors. There are many new topological results though because the topology of ${\bf R}^n$ is much richer.
Recall a vector field is a function $f \colon {\bf R}^2 \rightarrow {\bf R}^2$. It is called conservative if it is a gradient of a scalar function: $F = {\rm grad \hspace{3pt}} f$.
Theorem. Suppose $F=(P,Q)$ and $P_y=Q_x$ on region $D$. Then $F$ is conservative provided $D$ is simply connected.
Simply connected means that any closed curve can be contracted to point, without leaving the set. For example a circle is not simply connected.
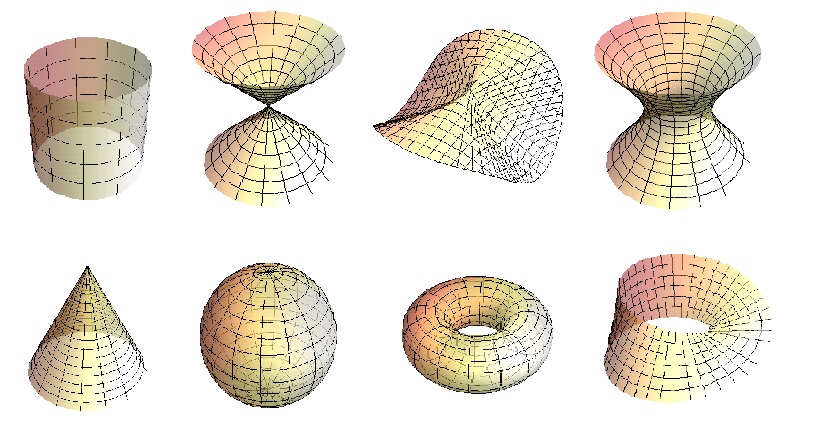
Exercise. Determine which ones of these surfaces are simply connected (sphere, torus, pretzel, cylinder, cone, plane, paraboloid, saddle, double cone).
Another topological topic in calculus is sequences.
To go deeper consider
Calculus is topology.