Homology of surfaces

Redirect to:

• Manifolds#Homology of curves and surfaces

Suppose $M$ is a surface, without boundary, path-connected, and compact (finitely many cells).

What do we know about the homology of $M$?

The $0$th homology $H_0$ is simple: $$H_0(M) = {\bf R}.$$

What about $H_1$? It varies:

$H_1($${\bf S}^2$) $= 0$,

$H_1($${\bf T}^2$) $= H_1($${\bf K}^2$) $= {\bf R}^2$,

$H_1({\bf T}^2$$\#$${\bf T}^2) = {\bf R}^3$, etc.

Turns out $H_2$ does not vary as much:

$H_2($${\bf S}^2$) $= H_2$(${\bf T}^2$) $= {\bf R}$,
$H_2($${\bf K}^2$) $= 0$.

Whether it's ${\bf R}$ or $0$ is determined by the orientability of the surface. Essentially, orientability tells us whether $M$ holds air.

As a surface $M$ has no $3$-cells, its $2$-boundary group is trivial: $$B_2(M) = \partial (C_3(M)) = \partial(0) = 0,$$ where $\partial$ is the boundary operator. Therefore, we only need to compute the $2$-cycle group: $$H_2(M) = Z_2(M) / B_2(M) = Z_2(M) / 0 = Z_2(M).$$

Suppose $C$ is a non-zero $2$-cycle and $$C = \displaystyle\sum_s d_s s, d_s \in {\bf R},$$ with summation over all faces $s$ in $M$, with some coefficients $d_s = 0$, possibly. Since $C$ is a cycle, the boundary $\partial C$ of $C$ is zero: $$\partial C = 0, {\rm \hspace{3pt} or}$$ $$\partial C = \displaystyle\sum_s d_s \partial s = 0.$$

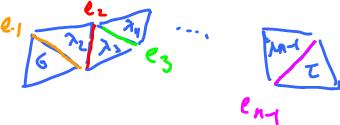
Since $\partial C$ consists of $1$-cells, let's take a look at the edges of $M$. Recall that in a surface, every edge is shared by exactly two faces ($2$-cells).

Therefore, every edge $e$ appears exactly twice in the above sum. Since $\partial \tau = 0$, every edge $e$ has to cancel. Hence

Lemma $1$. If edge $e$ is shared by faces $\sigma$ and $\tau$ then $$d_{\sigma} = \pm d_{\tau}.$$

Taking into account that $C$ is non-zero, there is a face $s$ with $d_s \neq 0$.

Since $M$ is connected, one can get from $s$ to any other face by following edge-face-edge-face... sequence:

By applying Lemma $1$ inductively, we obtain

Lemma. For any two faces $\sigma$ and $\tau$ in $M$, $$d_{\sigma} = \pm d_{\tau}.$$

Which sign? We have to look at the orientations of these faces.

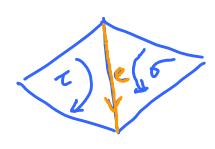
For example, suppose $$C = \sigma + \tau + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} \sigma, \tau$$ with orientation given here:

Then $$\begin{array}{l} \partial C &= e + e + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e \\ &\neq 0, \end{array}$$ because $e \neq 0$. Even if the orientation of $e$ is chosen opposite of this, the result is the same. Its orientation does not matter; what matters is the way $\sigma, \tau$ appear in $C$ (recall that the homology of a cell complex is independent of the orientations of its cells). Of course we could choose $$C = \sigma - \tau + \ldots,$$

which will cancel $e$, with these orientations. This answer, however is unsatisfactory because, what about the rest of the edges?

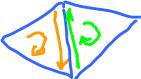
It's hard to enforce canceling by having opposite signs in the decomposition of $C$. It's easier to have the same signs for $\sigma$ and $\tau$ and then ensure cancellation by choosing appropriate orientations. Indeed, if we reverse the orientation of $\tau, e$ is canceled: $$\begin{array}{l} \partial C &= \partial ( \sigma + \tau + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} \sigma, \tau ) \\ &= e - e + {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e \\ &= {\rm \hspace{3pt} terms \hspace{3pt} w/o \hspace{3pt}} e. \end{array}$$

To keep track of all faces and edges and ensure canceling, we introduce this terminology. The orientations of two faces that share an edge will be called compatible if they induce the opposite orientations on the edge.

We can choose these orientations, if we deal with one edge at a time. But can we ensure that all pairs of faces have compatible orientations?

From what we know about orientable surfaces (they don't contain the Mobius band),

Theorem. A surface can be compatibly oriented iff it's orientable.

It follows

Corollary. Suppose $C$ is a non-zero $2$-cycle in an orientable connected surface $M$ and $$C = \displaystyle\sum_s d_s s, d_s \in {\bf R},$$ over all faces $s$ in $M$. Then for any two faces $\sigma$ and $\tau$ in $M$ $$d_{\sigma} = d_{\tau}.$$

From the corollary, it follows that $$C = d \displaystyle\sum_s s,$$ for some real $d$. It follows,

Theorem. For an orientable connected compact surface $M$ without boundary, the second homology group is generated by the sum of all faces in $M$: $$H_2(M) = {\bf R} = {\rm span}\{\displaystyle\sum_s s \}.$$

This generator is called the fundamental class of the surface.

Exercise. What if $M$ had boundary?

Theorem. For a non-orientable connected compact surface $M$ without boundary, $$H_2(M) = 0.$$

Exercise. Prove the theorem. Hint: the construction is the same as above: propagation of coefficients of faces in the decomposition of $C$.