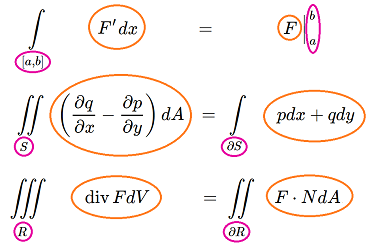This site is being phased out.
Exterior derivative
Redirect to:
We need to learn how to differentiate differential forms.
What may be the meaning of the derivative of a differential form?
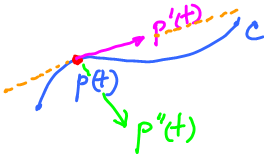
Consider motion on the plane along the curve $C$. Then $C$ is a parametric curve:
- $u = p(t)$, where $t$ represents time and $p(t) \in C$.
There are a couple of questions to consider.
Where's the velocity $p'(t)$?
It lives outside (exterior) the curve $C$! (Since they do not share units; i.e. if distances in $\mbox{span}(p(t))$ are measured in kilometers, then distances in $\mbox{span}(p'(t))$ are measured in kilometers per hour.)
What about the acceleration $p' '(t)$?
It lives outside (exterior) to ${\rm span}(p'(t))$!
Unless, of course, this is a straight line.
Note: This was a lame attempt of justification of the word "exterior" in "exterior derivative", that's all. Read Exterior algebra.
What we are used to is that the derivative of a function is also a function. But here we'll rely on the following:
Where does this come from?
Consider the Fundamental Theorem of Calculus, $$\displaystyle\int_{[a,b]} f'(x)dx = f\bigg|_{a}^b.$$ Remember, we don't integrate functions anymore. So, the two participants here are $f$, which is a $0$-form and $f'(x)dx$, which is a $1$-form. It is natural, then, to make the latter to serve as the "derivative" of the former. We call it the exterior derivative of $f$.
Another way to arrive to this conclusion is to look at the well-known relationship of differentials: $$df = f'(x)dx,$$ which is saying that the exterior derivative of the $0$-form $f$ is the $1$-form $f'(x)dx$.
In higher dimensions, given a $0$-form $f$, its exterior derivative is a $1$-form given by $$df = \nabla f dX = \nabla f \cdot (dx,dy,dz)$$ (like the dot product). Thus we have $df = f_x dx + f_y dy + f_z dz$, where $f_x$, $f_y$, and $f_z$ are the partial derivatives of $f$.
To summarize, the exterior derivative operator, $d$, is a function $$d \colon \Omega^0 \rightarrow \Omega^1 .$$
Now, we take a broader look at the fundamental theorem of calculus and the rest of theorems of vector calculus:
We notice in each formula that:
- in the right-hand side we have very general integrands, while
- the integrands in the left-hand sides are messy but they are, though some complicated computations, derived from those in the right-hand side.
The idea is:
If the idea is implemented, these theorems will be just instances of a more general theorem, a theorem about differential forms. It is called the Stokes theorem: $$\displaystyle\int_R d \omega = \displaystyle\int_{\partial R} \omega.$$ Here $R$ is a $(k+1)$-dimensional region while its boundary $\partial R$ is $k$-dimensional.
Thus we arrive to a similar idea about the relation of any form and its derivative:
So, if the input of $d$ is a $0$-form, then the output is a $1$-form. Likewise, if the input of $d$ is a $1$-form, then the output is a $2$-form.
Before we proceed, let's make an observation by taking advantage of this formula that wonderfully connects topology and calculus.
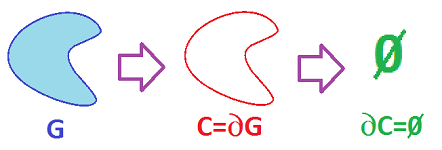
It is known that "boundaries have no boundaries":
- the end-points of a curve have empty boundary;
- the boundary of a region is a curve with no end-points;
- the boundary of a solid is a surface with no edge curve, etc.
In other words, $$\partial \partial G = \emptyset,$$ for any region $G$.
Applying the Stokes Theorem twice we obtain: $$\displaystyle\int_R dd \varphi = \displaystyle\int_{\partial R} d\varphi =\displaystyle\int_{\partial\partial R} \varphi =\displaystyle\int_{\emptyset} \varphi =0.$$ So the integral of the form $dd\varphi$ is $0$ over any region. It follows that $dd\varphi = 0$, or simply $$dd=0.$$ We will prove this identity algebraically below.
Definition and computations of the exterior derivative
Below we assume that all functions are differentiable.
We already know the meaning of the exterior derivative of $0$-forms.
Next, $1$-forms. We start with the exterior derivative of multiples of the basis elements of $\Omega ^1$: $d(Adx)=?$, where $A$ is a function. Let's try the "product rule": $$d(Adx)=dAdx+Adxdx$$ $$=dAdx,$$ by antisymmetry. So we end up differentiating only the coefficient.
Now a general $1$-form in $3$-space: $$\varphi = F dx + G dy + H dz.$$ Then we using additivity to obtain: $$\begin{align*} d \varphi &= d(F dx + dG dy + dH dz) \\ &= d(F dx) + d(G dy) + d(H dz) \\ &= (dF dx +Fddx)+ (dG dy+Gddy) + (dH dz +Hddz)\\ &= (dF dx +0)+ (dG dy+0) + (dH dz +0)\\ &= (F_x dx + F_y dy + F_z dz)dx+(G_x dx + G_y dy + G_z dz)dy+(H_x dx + H_y dy + H_z dz)dz \\ &= (F_y dy \hspace{1pt} dx + F_z dz \hspace{1pt} dx) + (G_x dx \hspace{1pt} dy + G_z dz \hspace{1pt} dy) + (H_x dx \hspace{1pt} dz + H_y dy \hspace{1pt} dz) \\ &= (G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx. \end{align*}$$ We recognize these coefficients as those of the curl: $$curl<F,G,H> = <G_x - F_y,H_y - G_z,F_z - H_x>.$$ We must be on the right track!
Now we define the exterior derivative, computationally, for the general case.
Definition: If $\varphi \in \Omega^k$, it is a linear combination of the basis elements of $\Omega^k$. Then the exterior derivative of $\varphi$ is a $(k+1)$-form $d \varphi \in \Omega^{k+1}$ obtained from this linear combination by applying $d$ to each of the coefficient functions.
We now compute the exterior derivative for forms of various degrees, in $3$-space.
We will use the formula for $0$-forms: $d F^0 = F_x dx + F_y dy + F_z dz$. We recognize these coefficients as those of the gradient: $$grad \hspace{1pt} F = <F_x, F_y,F_z>.$$
Consider a $2$-form which is a linear combination of $dxdy$, $dydz$, and $dzdx$ whose coefficients are the functions to differentiate. Let $$\varphi = Adxdy + Bdydz + Cdzdx.$$ Then $$\begin{align*} d \varphi &= dA dx dy + dB dy dz + dC dz dx\\ &= (A_xdx+A_ydy+A_zdz)dxdy+...\\ &= (A_x dxdxdy + A_y dydxdy + A_z dzdxdy)+... \\ &= (0+0+A_z dzdxdy)+...\\ &= A_z dzdxdy + B_x dxdydz + C_y dydzdx\\ &= (A_z + B_x + C_y )dxdydz.\\ \end{align*}$$ We recognize the coefficient as the divergence: $$div < B,C,A> = B_x + C_y + A_z.$$ Each term in the form is associated with the missing variable: $dxdy \rightarrow z$.
Same for dimension $2$: $$\begin{align*} d \varphi &= dF dx + dG dy \\ &= (F_x dx + F_y dy)dx+(G_x dx + G_y dy )dy \\ &= F_y dy \hspace{1pt} dx + G_x dx \hspace{1pt} dy \\ &= (G_x - F_y) dx \hspace{1pt} dy. \end{align*}$$
Now for degree $3$. If $\varphi = F dx \hspace{1pt} dy \hspace{1pt} dz$, then $$\begin{align*} d \varphi &= dF \cdot dx \hspace{1pt} dy \hspace{1pt} dz \\ &= (F_x dx + F_y dy + F_z dz) dx \hspace{1pt} dy \hspace{1pt} dz \\ &= F_x dx \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz + F_y dy \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz + F_z dz \hspace{1pt} dx \hspace{1pt} dy \hspace{1pt} dz \\ &= 0 + 0 + 0=0. \end{align*}$$
What about forms in ${\bf R}^n$? If $\varphi = F dx_1 \ldots dx_n$, then $d \varphi = 0$ (same proof!).
Summary of formulas.
- Degree $0$: $d F ^0 = F_x dx + F_y dy + F_z dz$.
- Degree $1$: $d(F dx + G dy + H dz) = (G_x - F_y) dx \hspace{1pt} dy + (H_y - G_z) dy \hspace{1pt} dz + (F_z - H_x) dz \hspace{1pt} dx$.
- Degree $2$: $d(F dx \hspace{1pt} dy + G dy \hspace{1pt} dz + H dz \hspace{1pt} dx)=(F_z + G_x + H_y) dx \hspace{1pt} dy \hspace{1pt} dz.$
- Degree $3$: $d\varphi ^3=0$.
Example: Let $$\varphi = x^2ydx \hspace{1pt} dy + xy dy \hspace{1pt} dz.$$ Then $$\begin{align*} d \varphi &= d(x^2y) dx \hspace{1pt} dy + d(xy) dy \hspace{1pt} dz \\ &= (2xy dx + x^2 dy) dx \hspace{1pt} dy + (y dx + x dy) dy \hspace{1pt} dz \\ &= 2xy dxdxdy - x^2 dx \hspace{1pt} dy \hspace{1pt} dy + y dx \hspace{1pt} dy \hspace{1pt} dz + xdy \hspace{1pt} dy \hspace{1pt} dz \\ &= y dx \hspace{1pt} dy \hspace{1pt} dz. \end{align*}$$
Another way to write the definition is this. Given
- $\varphi = A dX \in \Omega^k$
where $A$ is continuously differentiable function and $dX$ is a basis element of $ \Omega^k$ (could be $dx,dy$, or $dxdy,dydz$, etc). Then, we define
- $d\varphi = dA \wedge dX$ and
then extend this definition to sums of terms of this kind.
We defined the exterior derivative in terms of its coefficient functions. The question remains, why is the definition independent from the choice of coordinate system?
Vector spaces in calculus
The main contribution of linear algebra to calculus is of course linearization: if a function $f\colon {\bf R}^n \rightarrow {\bf R}$ is differentiable at $a$ then $f$ has the best affine approximation at $a$. Note: The linear part of this approximation is $df(a)$!
But there is more.
Recall the notation:
- $f \in C^0({\bf R})=C({\bf R})$ if $f:{\bf R}^n \rightarrow {\bf R}$ is continuous;
- $f \in C^1({\bf R})$ if the derivative of $f$ (exists and) is continuous;
- $f \in C^2({\bf R})$ if $f', f' '$ (exist and) are continuous;
- ...
- $f \in C^k({\bf R})$ if $f', \ldots, f^{(k)}$ (exist and) are continuous;
- $f \in C^{\infty }({\bf R}) $ if $f', \ldots, f^{(k)},\ldots$ (exist and) are continuous.
Proposition: If $f \in C^{k}({\bf R})$, then $f' \in C^{k-1}({\bf R})$, for $k \neq 0$ and $k \neq \infty$.
Twice continuously differentiable, $C^2$, satisfy nice properties. However, other classes are also of interest; in particular, square integrable functions, $L_2$. A possible notation of these spaces is: $$C^2\Omega ^k(R),L_2\Omega ^k(R).$$
We use the same terminology (continuity and differentiability) with differential forms when we speak about their coefficient functions.
Linear algebra provides a nice, bird's-eye view of elementary calculus with this diagram of vector spaces and linear operators: $$...\xrightarrow{\frac{d}{dx}} C^3({\bf R}) \xrightarrow{\frac{d}{dx}}C^2({\bf R}) \xrightarrow{\frac{d}{dx}}C^1({\bf R}) \xrightarrow{\frac{d}{dx}}C^0({\bf R}).$$ If we replace ${\bf R}$ with a subset $X$ we can relate the class of antiderivatives, i.e., $\frac{d}{dx}^{-1}$, to the topology of $X$. This is a starting point of "de Rham cohomology".
Unfortunately, this neat picture of arrows going from a function to its derivative function to the second derivative etc is purely $1$-dimensional. It breaks down if we try to replace ${\bf R}$ with ${\bf R}^n$. Indeed, the derivative of a function of $n$ variables, its gradient, is a vector field, which is an entity of a nature entirely different from that of the function itself.
Exterior calculus, which is calculus of differential forms and their exterior derivatives, doesn't have this problem. This is our diagram of vector spaces and linear operators: $$ \Omega^0 ({\bf R}^n) \stackrel{d}{\rightarrow} \Omega^1 ({\bf R}^n) \stackrel{d}{\rightarrow} \Omega^2 ({\bf R}^n)\stackrel{d}{\rightarrow} \Omega^3 ({\bf R}^n)\stackrel{d}{\rightarrow} \ldots .$$ As long as the functions involved are differentiable, this scheme works in any dimension.
Note: $\dim \Omega ^k (p\in {\bf R}^n) = {n \choose k}.$
More generally, we have $$ \Omega^0 (R) \stackrel{d}{\rightarrow} \Omega^1 (R) \stackrel{d}{\rightarrow} \Omega^2 (R)\stackrel{d}{\rightarrow} \Omega^3 (R)\stackrel{d}{\rightarrow} \ldots ,$$ where $R$ is an open subset of ${\bf R}^n$. It is called the de Rham complex. This diagram is supposed to contain all information about the topology of $R$ via so-called de Rham cohomology.
See Properties of the exterior derivative next.