Homology in Calculus

Redirect to:

• Homology as an equivalence relation#Homology in calculus

In order to make this study independent from a lengthy development of point-set topology, we will initially limit ourselves to the study of

subsets of a Euclidean space.

In the very beginning of our study of Topology we are interested in the following visually simple features:

• cuts/components,
• tunnels/holes,
• voids/bubbles, etc.

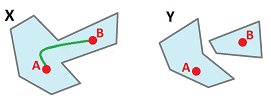
First components.

The corresponding mathematical concept is connectedness: $X$ is path-connected if any two points can be connected by a path:

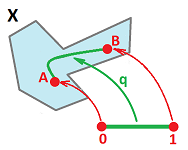
First what is a "path"? It is a parametric curve (like the circle $x=\cos t, y=\sin t$.)

Then we state that $X$ is connected if for any two points $A, B$ in $X$ there is a continuous function $q \colon [0,1] \rightarrow X$ such that $q(0)=A$, $q(1)=B$.

Here's a related theorem from calc 1.

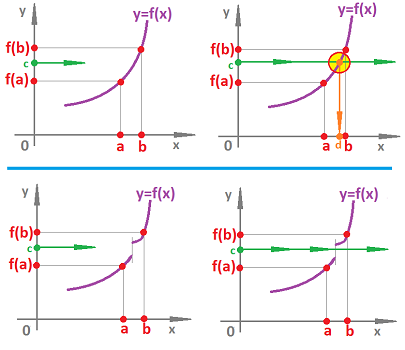
Intermediate Value Theorem. Suppose $f \colon [a,b] \rightarrow {\bf R}$ is continuous. Then for any $c$ between $f(a)$ and $f(b)$ there is $d \in [a,b]$ such that $f(d) = c$.

Question: What does this have to do with path-connectedness?

Answer: The image of a connected interval is a connected interval, under a continuous function:

Next, let's test how well you know calculus.

Question: What is the antiderivative of $1/x$?

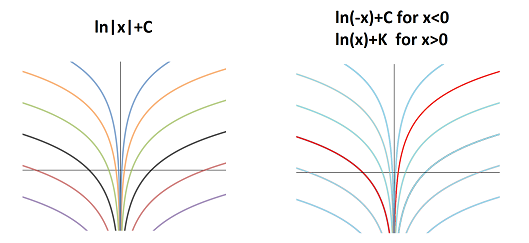
Calculus 1 "answer": $F(x)=\ln|x|+C.$

Wrong!

Why wrong? Hint: $1/x$ undefined at $0$.

But first, what is our formula supposed to mean?

Recall that the $+C$ in the formula is supposed indicate that we have captured infinitely many (one for each real number $C$) antiderivatives. We also imply that we have then all!

And we would -- with any other, continuous, function $f$:

the set of all antiderivatives of $f$ is $F_C(x)=F_0(x)+C, C\in {bf R}$,

where $F_0$ is any antiderivative of $f$.

But $1/x$ is defined on $(-\infty, 0)$ and $(0, +\infty)$, separately!

Therefore, we can, correctly, solve this problem separately on each:

• $\ln(-x)+C$ on $(-\infty, 0)$, and
• $\ln(x)+C$ on $(0, +\infty)$.

But if we want to combine these sets into one, we realize that, every time, the constants might be different! The reason is that they have nothing to do with each other as their intervals are disconnected from each other.

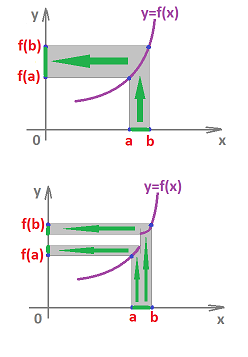
Let's visualize the wrong answer on the left and the right on the right:

The image on the left suggests that the answers are even functions -- one for each color. The one on the right shows only one answer and its two branches don't have to match!

Algebraically, $$ F(x)=F_{C,K}(x) = \begin{cases} \ln(-x)+C & \text{ if } x \in (-\infty, 0) \\ \ln(x)+K & \text{ if } x \in (0, +\infty) \end{cases} $$ One can verify that this is an antiderivative of $1/x$ by differentiation.

This family of functions isn't parametrized by the reals ${\bf R}$ anymore, but, with two parameters, by ${\bf R}^2$. The exponent reflects the number of components of the domain!

Question: But is $F$ continuous?

Hmmm, it doesn't look continuous...

Answer: Yes, it is!

Exercise. Verify -- point-wise.

This is the disconnected reality:

Here's another

"Theorem" from Calc 1. If $F'=0$ then $F$ is constant.

...not the whole story, as we just saw.

Let's restate properly.

Theorem. Given a function $F:X \rightarrow {\bf R}$, where $X$ is an open subset of ${\bf R}$, and

• $F$ is differentiable on $X$,
• $F'(x)=0$ for all $x \in X$.

Then $F$ is constant.... provided $X$ is connected.

In fact, here $X$ is a union of open intervals and, for the theorem to hold, it should be a single interval. A very important part of a topology course should be the study of:

interaction between Calculus and Topology.

As follows:

• → Given $X$, if we know its topology, then we know a lot about the calculus on $X$.
• ← Given calculus on $X$, it tells us a lot about the topology of $X$.

So far, the idea has been applied to a very limited extent:

1. only connectedness, and
2. only on the real line.

Sidenote: What about connectedness in calculus on the plane? For functions of two variables there is no such thing as antiderivative and the above construction doesn't apply. This is one of the reason why one uses differential forms for a similar analysis. $\square$

Less precise is the discussion in calculus of issues related to holes...

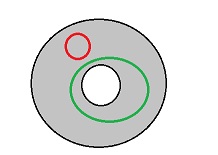
The corresponding mathematical concept is simple connectedness: $X$ is simply connected if every closed curve $C$ can be "contracted" to a point without leaving $X$.

Recall a vector field is a function $f \colon {\bf R}^2 \rightarrow {\bf R}^2$. It is called conservative if it is a gradient of a scalar function: $F = {\rm grad \hspace{3pt}} f$.

Theorem. Suppose $F=(P,Q)$ and $P_y=Q_x$ on region $D$. Then $F$ is conservative provided $D$ is simply connected.

Simply connected means that any closed curve can be contracted to point, without leaving the set. For example a circle is not simply connected.

The main conclusion is that the integral is path-independent! The reason is that in a simply connected region you can't go around a hole which might affect the value of the integral.

Sidenote: this is also related to the Cauchy Residue Theorem in complex analysis. $\square$

Consider also Calculus is topology.