Vietoris-Rips complex

Redirect to:

• Simplicial complexes#Data as a point cloud

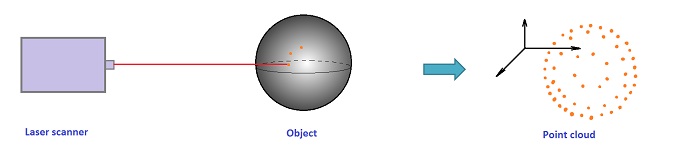
Point clouds

Consider this object:

It looks like a triple torus.

But what if we zoom in?

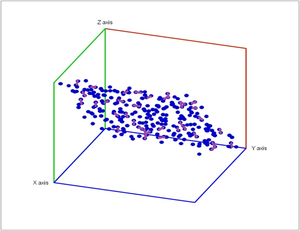
We realize that the "object" is just dots suspended in space! It is called a point cloud.

Another example:

Where do point clouds come from?

They may come from scanning:

They also may come from data...

Topological data analysis

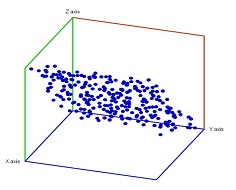
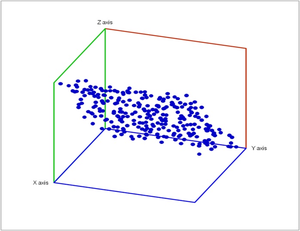
Suppose we have conducted 1000 experiments with a set of 100 various measurements in each. Then each experiment is a string of 100 numbers or simply a vector of dimension 100. The result is a collection of disconnected 1000 points, called a point cloud, in the 100-dimensional Euclidean space.

It is impossible to visualize this data as any representation is limited to dimension 3 (by using colors one gets 6, time 7). Yet we still need to answer questions about the object behind the point cloud:

• Is it one piece or more?
• Is there a tunnel?
• Or a void?
• And what about possible 100-dimensional topological features?

Through clustering (and related approaches) statistics answers the first question. The rest need a topological treatment.

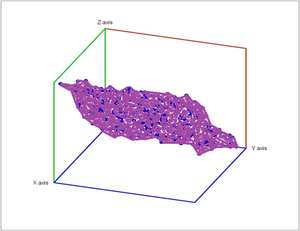
Just as important as these "global" properties may be the local topology of the data. For example, in both of the images above the datasets are $3$-dimensional but what's behind is $2$-dimensional (i.e., a surface). This is called manifold learning and is related to dimensionality reduction.

Some issues with the traditional approaches to manifold learning are:

• They rely on local linearity of the dataset and may fail when the manifold is highly curved.
• They assume that the dataset is a manifold in the first place. There are numerous examples of datasets where this assumption is violated, such as graphs.
• They assume that the topological space behind the data set inherits the topology of the Euclidean space that is supposed to contain it. The possibility of non-Euclidean topology is ignored.

How do we understand the topology of the object is behind the point cloud?

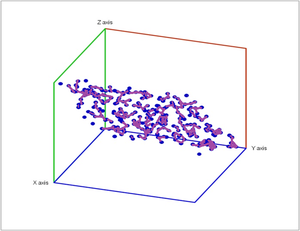
Vietoris-Rips construction

Here's one approach...

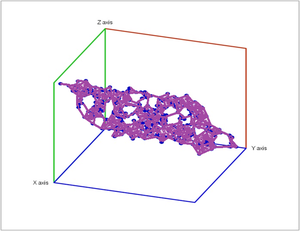
Given $r>0$, we deem any two points that lie within $r$ from each other as "close". In this case, this pair of points is connected by an edge. Further, if three points are "close", pairwise, to each other, we add a face spanned by these points. If there are four, we add a tetrahedron, and, finally, any $d+1$ "close" points create a $d$-cell.

The result is a simplicial complex $K$ for each $r$.

Together, they form a sequence called filtration as a sequence of "nested" simplicial complexes: $$K¹ ↪ K² ↪ K³ ↪ K⁴ ↪ … ↪ K^s,$$ where the arrows are the inclusions.

In order to understand the topology of the object that produced the filtration we look at a sequence of homology groups connected by homomorphisms: $$H_{\ast}(K^{1})\rightarrow H_{\ast}(K^{2})\rightarrow\ldots\ \rightarrow H_{\ast}(K^{s})\longrightarrow 0, $$ generated by this sequence.

This is the homology.

Dimension $0$: $${\bf Z}\times {\bf Z}\rightarrow {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z}\times {\bf Z} \rightarrow {\bf Z} \rightarrow 0. $$ Dimension $1$: $$0\rightarrow 0 \rightarrow {\bf Z} \rightarrow {\bf Z} \rightarrow 0 \rightarrow 0. $$

Exercise: Find the homology of the inclusions.

A similar construction is possible that uses the density of points instead of the distances.