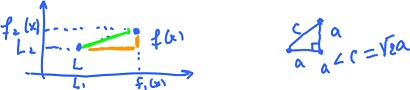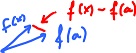This site is being phased out.
Parametric curves
Contents
Introduction
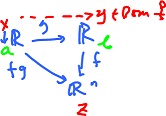
Simply put, curves are functions $F: {\bf R} {\rightarrow} {\bf R}^q$ (can also be defined on a subset of ${\bf R}$).
Examples. Linear functions $f: {\bf R} {\rightarrow} {\bf R}^n.$
- $f(t) = v \cdot t$, a motion along a vector $v \in {\bf R}^n$ (constant speed), then $f(0) = 0, f(1) = 1$.
- $f(t) = v \cdot t + b$, with $b \in {\bf R}^n$
- backward motion: $g(t) = - v \cdot t = v \cdot (-t)$
Here
- $t$ is thought of as time,
- $f(t)$ is thought of as the position in space at time $t$.
Just the space happens to be $n$-dimensional...
Just as before we'll need limits in order to define and study
More generally, we consider in dimension 2:
$$f(t) = (f_1(t), f_2(t)),$$
then
Examples. Specifically, consider the following. (1) circular motion, cntered at 0: $f(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t)$ backward: $f(t) = ({\rm cos \hspace{3pt}} (-t), {\rm sin \hspace{3pt}}(-t)),$ radius $r$: $f(t) = r \cdot ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t)$, centered at $(a,b)$: $f(t) = (a,b) + r \cdot ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t)$ accelerated motion: $f(t) = ({\rm cos \hspace{3pt}} t^2, {\rm sin \hspace{3pt}} t^2)$
etc
(2) parabola: $f(t) = (t, t^2)$, $f(t)$ parametrizes the parabola: $y = x^2$
$$f: {\bf R} {\rightarrow} {\bf R}^3$$
(3) circle in space $f(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t, 0)$ (in $xy$-plane)
(4) $f(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t, t)$ corresponding to $(x, y, z)$
Limits
Question asked in Calc 1: For $f: {\bf R} {\rightarrow} {\bf R}^n$, what happens to $f(x)$ (location) as $x \rightarrow a$ (time)?
Definition. The answer to this question is written as
in which case $L$ is called the limit of $f$ as $t$ approaches $a$. Algebraically, we define the (?) limit as the (?) number that satisfies the following:
Note that $||f(t) - L||$ is a number (see Norm).
Example. Let $f(t) = (2x, 3x), a = 1$. Then $$\begin{array}{} ? = L &= \displaystyle\lim_{t \rightarrow a} f(t) \\ &= \displaystyle\lim_{t \rightarrow a} (2x, 3x) \\ &= (2 \cdot 1, 3 \cdot 1) {\rm \hspace{3pt} (plug \hspace{3pt} in \hspace{3pt}} x = 1) \\ &= (2, 3), \end{array}$$
so $L = (2,3)$.
To make this more precise we follow the definition: $$\begin{array}{} || f(t) - L || &= || (2x, 3x) - (2, 3) || \\ &= || (2x - 2, 3x - 3) || \\ &= || 2(x - 1) - 3(x - 1) || \\ &= ( (2(x - 1))^2 + (3(x - 1))^2 )^{\frac{1}{2}} \\ &= ( 4(x - 1)^2 + 9(x - 1)^2 )^{\frac{1}{2}} \\ &= ( (x - 1)^2 (4 + 9) )^{\frac{1}{2}} \\ &= ( (x - 1)^2 \cdot 13 )^{\frac{1}{2}} \\ &= | x - 1 | \sqrt{13} \\ &\rightarrow 0 \cdot \sqrt{13} = 0 {\rm \hspace{3pt} as \hspace{3pt}} x \rightarrow 1, \end{array}$$
since $x {\rightarrow} 1$ means $x - 1 {\rightarrow} 0$ and $| x - 1 | {\rightarrow} 0$ (see Calc 1).
Example. Let $f(x) = ({\rm sin \hspace{3pt}} x, {\rm cos \hspace{3pt}} x)$, what if $x {\rightarrow} 0$?
Answer: $f(x) {\rightarrow} (0, 1)$.
Let's confirm that.
Claim: $|| ({\rm sin \hspace{3pt}} x, {\rm cos \hspace{3pt}} x) - (0, 1) || = || ({\rm sin \hspace{3pt}} x, {\rm cos \hspace{3pt}} x - 1) || {\rightarrow} 0$ as $x {\rightarrow} 0$.
Why? Let's take a more general case.
If $f(x) = (f_1(x), f_2(x))$, for $f: {\bf R} {\rightarrow} {\bf R}^2$ then
$$\displaystyle\lim_{x \rightarrow a} f(x) = (\displaystyle\lim_{x \rightarrow a} f_1(x),\displaystyle\lim_{x \rightarrow a} f_2(x) ).$$
(1) Indeed, suppose $f(x) {\rightarrow} L$ as $x {\rightarrow} a$, where $L = (L_1, L_2)$ and $f: {\bf R} {\rightarrow} {\bf R}^2$.
Since $f = (f_1, f_2)$, we need to show that $f_1 {\rightarrow} L_1$ as $x {\rightarrow} a$ and $f_2 {\rightarrow} L_2$ as $x {\rightarrow} a$. Let's do that. We have $|| f(x) - L || {\rightarrow} 0$ as $x {\rightarrow} a$ by definition, i.e.
$$( (f_1(x) - L_1)^2 + (f_2(x) - L_2)^2 )^{\frac{1}{2}} {\rightarrow} 0.$$
We want to show that the above limit implies these: $(f_1(x) - L_1)^2 {\rightarrow} 0$ and $(f_2(x) - L_2)^2 {\rightarrow} 0$ as $x {\rightarrow} a$.
Now $0 \leq | f_1(x) - L_1 | \leq ( (f_1(x) - L_1)^2 + (f_2(x) - L_2)^2 )^{\frac{1}{2}} {\rightarrow} 0$. By the Squeeze Theorem, we have
Thus, if $f_1(x) {\rightarrow} L_1$ and $f_2(x) {\rightarrow} L_2,$ then $f(x) {\rightarrow} (L_1, L_2)$.
(2) The converse of (1):
$$\begin{array}{} 0 &\leq ( (f_1(x) - L_1)^2 + (f_2(x) - L_2)^2 )^{\frac{1}{2}} {\rm (green)} \\ &\leq \sqrt{2} {\rm max}\{ |f_1(x) - L_1|, |f_2(x) - L_2| \} {\rightarrow} 0 {\rm (orange)}. \end{array}$$
By the Squeeze Theorem, it follows $|| f(x) - L || {\rightarrow} 0$ as $x {\rightarrow} a$.
We have proven the following.
Theorem. $(f_1(x), f_2(x)) {\rightarrow} (L_1, L_2)$ if and only if $f_1(x) {\rightarrow} L_1$ and $f_2(x) {\rightarrow} L_2$.
Review exercise. Given $$L = \left| \begin{array}{r} 1 & 1 \\ 1 & -1 \end{array} \right|$$
compute: $$L^2 = \left| \begin{array}{r} 1 & 1 \\ 1 & -1 \end{array} \right| \left| \begin{array}{r} 1 & 1 \\ 1 & -1 \end{array} \right| = \left| \begin{array}{} 2 & 0 \\ 0 & 2 \end{array} \right|$$
Two cases:
- $m$ even, $m = 2n$:
$$L^{2n} = (L^2)^n = \left| \begin{array}{} 2 & 0 \\ 0 & 2 \end{array} \right|^n = \left| \begin{array}{} 2^n & 0 \\ 0 & 2^n \end{array} \right|$$
- $m$ odd, $m = 2n + 1$:
$$L^{2n+1} = L^{2n} L = \left| \begin{array}{} 2^n & 0 \\ 0 & 2 \end{array} \right| \left| \begin{array}{} 1 & 1 \\ 0 & 2^n \end{array} \right| = \left| \begin{array}{r} 2^n & 2^n \\ 2^n & -2^n \end{array} \right|$$
- $m$ even, $m = 2n$:
$$L^m e_1 = \left| \begin{array}{} 2^n & 0 \\ 0 & 2^n \end{array} \right| = \left| \begin{array}{} 1 \\ 0 \end{array} \right| = \left| \begin{array}{} 2^n \\ 0 \end{array} \right|$$
- $m$ odd, $m = 2n + 1$:
$$L^m e_1 = \left| \begin{array}{r} 2^n & 2^n \\ 2^n & -2^n \end{array}\right| = \left| \begin{array}{} 1 \\ 0 \end{array}\right| = \left| \begin{array}{} 2^n \\ 2^n \end{array}\right|$$
- $n = 1, 2, 3,...:$
$$\left| \begin{array}{} 2 \\ 0 \end{array}\right|, \left| \begin{array}{} 2 \\ 2 \end{array}\right|, \left| \begin{array}{} 4 \\ 0 \end{array}\right|, \left| \begin{array}{} 4 \\ 4 \end{array}\right|$$
Definition. For a function $f: {\bf R} {\rightarrow} {\bf R}^n$ we write $\displaystyle\lim_{x \rightarrow a} f(x) = L$ if $\displaystyle\lim_{x \rightarrow a} || f(x) - L || = 0.$
So we define limits of functions of several variables by means of the limit for functions of one variable, from Calc 1. This is typical in vector calculus.
To generalize the above theorem.
Theorem. Let $f: {\bf R} {\rightarrow} {\bf R}^n$ be a function. Then
where $f = (f_1, f_2, ..., f_n), L = (L_1, L_2, ..., L_n).$
Theorem (Properties of Limits). Suppose $\displaystyle\lim_{x \rightarrow a} f(x) = L,\displaystyle\lim_{x \rightarrow a} g(x) = M$. Then
- $\displaystyle\lim_{x \rightarrow a} ( f(x) + g(x) ) = L + M$
- $\displaystyle\lim_{x \rightarrow a} ( \alpha f(x) ) = \alpha L, \alpha \in {\bf R}$
- $\displaystyle\lim_{x \rightarrow a} < f(x), g(x) > = < L, M >$
- $\displaystyle\lim_{x \rightarrow a} || f(x) || = || L || for f: {\rightarrow} {\bf R}^n.$
Proof The idea is to treat the functions coordinate-wise.
- $\displaystyle\lim_{x \rightarrow a} ( f_i(x) + g_i(x) ) = L_i + M_i$
- $\displaystyle\lim_{x \rightarrow a} ( \alpha f_i(x) ) = \alpha L_i$
$$\begin{array}{} \displaystyle\lim_{x \rightarrow a} < f(x), g(x) > &= \displaystyle\lim_{x \rightarrow a} ( f_1(x) g_1(x) + f_2(x) g_2(x) + ... + f_n(x) g_n(x) ) \\ &=\displaystyle\lim_{x \rightarrow a} f_1(x) ⋅\displaystyle\lim_{x \rightarrow a} g_1(x) + ... \\ &= L_1 M_1 + L_2 M_2 + ... + L_n M_n {\rm \hspace{3pt} by \hspace{3pt} sum \hspace{3pt} rule \hspace{3pt} and \hspace{3pt} product \hspace{3pt} rule} \\ &= < L, M > \end{array}$$
$$\begin{array}{} \displaystyle\lim_{x \rightarrow a} || f(x) || &= \displaystyle\lim_{x \rightarrow a} ( < f(x), f(x) > )^{\frac{1}{2}} \\ &= (\displaystyle\lim_{x \rightarrow a} < f(x), f(x) > )^{\frac{1}{2}} {\rm \hspace{3pt} since \hspace{3pt}} \sqrt{} {\rm \hspace{3pt} is \hspace{3pt} continuous} \\ &= ( < L, L > )^{\frac{1}{2}} \\ &= || L || \end{array}$$
The last one deserves a special attention. Let's restate it first:
Theorem.
This theorem can be seen as equivalent to the continuity of the norm. Now, what about the converse?
The converse does not hold, i.e. from $\displaystyle\lim_{x \rightarrow a} || f(x) || = || L ||$ does not follow $\displaystyle\lim_{x \rightarrow a} f(x) = L$. To illustrate, you don't have to use vectors...
Example. Suppose $n = 1$ and $f$ is the sign function. Then $f(x) {\rightarrow} -1$, then $| f(x) | {\rightarrow} | -1 | = 1$.
Then $\displaystyle\lim_{x \rightarrow 0} f(x)$ does not exist, whereas $\displaystyle\lim_{x \rightarrow 0} | f(x) | = \displaystyle\lim_{x \rightarrow 0} 1 = 1.$
A partial converse holds for $L = 0$:
Theorem. If $\displaystyle\lim_{x \rightarrow a} || f(x) || = 0$ then $\displaystyle\lim_{x \rightarrow 0} f(x) = 0.$
Why? We have $\displaystyle\lim_{x \rightarrow 0} | || f(x) || - 0 | = \displaystyle\lim_{x \rightarrow 0} || f(x) || = 0$ and $\displaystyle\lim_{x \rightarrow 0} || f(x) - 0 || = \displaystyle\lim_{x \rightarrow 0} || f(x) || = 0.$
Same!
Continuity
As always in vector calculus, definitions follow the corresponding ones from Calc 1.
Definition. A function $f: {\bf R} {\rightarrow} {\bf R}^n$ is continuous at $x = a$ if
$$\displaystyle\lim_{x \rightarrow a} f(x) = f(a)$$
Which can be rewritten as
- $|| f(x) - f(a) || {\rightarrow} 0$ or
- $f(x) - f(a) {\rightarrow} 0$ or
- $f(x) {\rightarrow} f(a)$.
Theorem (Algebraic properties of continuous functions). Let $f: {\bf R} {\rightarrow} {\bf R}^n$, $g: {\bf R} {\rightarrow} {\bf R}^n$ be continuous at $x = a$. Then
- $f + g$ is continuous at $a$,
- $df$ is continuous at $a$,
- $< f, g >$ is continuous at $a$,
- $| f |$ is continuous at $a$.
Proof Using the limit theorem part 1 above, $$\begin{array}{} \displaystyle\lim_{x \rightarrow a} ( f(x) + g(x) ) &=\displaystyle\lim_{x \rightarrow a} f(x) +\displaystyle\lim_{x \rightarrow a} g(x) \\ &= f(a) + g(a) {\rm \hspace{3pt} using \hspace{3pt} continuity \hspace{3pt} of \hspace{3pt}} f, g \\ &= ( f + g )(a). QED \end{array}$$
A special algebraic property is that continuity is preserved under compositions. Recall the definition.
Let $f: {\bf R} {\rightarrow} {\bf R}^n, g: {\bf R} {\rightarrow} {\bf R}$. Then the composition $fg: {\bf R} {\rightarrow} {\bf R}^n$ is defined for each $x$ in the domain of $g$:
$$fg(x) = f( g (x) ).$$
Assume that range of $g$ lies in the domain of $f$. If $y = g(x) {\rightarrow} b$ as $x {\rightarrow} a$, $z = f(y) {\rightarrow} L$ as $y {\rightarrow} b$, then
$$fg {\rightarrow} L {\rm \hspace{3pt} as \hspace{3pt}} x {\rightarrow} a.$$
This comes from the theorem about coordinate-wise limits above.
Theorem (Compositions of continuous functions).
(5) Let $f: {\bf R} {\rightarrow} {\bf R}^n, g: {\bf R} {\rightarrow} {\bf R}$ be continuous and assume range $g \subset$ domain $f$. If $g$ is continuous at $x = a$ and $f$ is continuous at $y = b = g(a)$, then $fg$ is continuous at $x = a$.
Let's restate the property.
$$\displaystyle\lim_{x \rightarrow a} f( g(x) ) = f(b)$$
since
$$\displaystyle\lim_{x \rightarrow a} g(x) = b_z, \displaystyle\lim_{y \rightarrow b} f(y) = L, \displaystyle\lim_{x \rightarrow a} f( g(x) ) = L.$$
Hence
$$f(b) = f(\displaystyle\lim_{x \rightarrow a} g(x) ) = f( g(a) ).$$
What if $f$ is the norm?
Example. Consider $f(y) = {\rm sin \hspace{3pt}} y$ continuous. Here we have
$$\displaystyle\lim_{x \rightarrow 33} {\rm sin \hspace{3pt}} ( e^x + x^2 )^{\frac{1}{2}} = {\rm sin \hspace{3pt}}( \displaystyle\lim_{x \rightarrow 33} ( e^x + x^2 )^{\frac{1}{2}} ),$$
and because $\sqrt{}$ is continuous, we obtain
$${\rm sin \hspace{3pt}} ( \displaystyle\lim_{x \rightarrow 33} ( e^x + x^2 ))^{\frac{1}{2}} = ...$$
Tangents
Recall some motivation for differential calculus, from Calc 1.
We want to study motion. Some questions we may ask are:
- On a winding road what is the direction of the headlights?
- Where does the rock go when released from the slingshot?
The answer is consider the tangents.
For the slingshot, we write $$f(x) = ( 1 - x^2 )^{\frac{1}{2}}$$ the graph of which is the circle. Then we differentiate and find the tangent line to the circle at any point: the slope of the tangent line is equal to the value of the derivative of $f$ at the point.
This is the way the issue is handled in Calc 1.
There are some issues though. One is that strictly speaking the circle is given by $$f(x) = \pm ( 1 - x^2 )^{\frac{1}{2}},$$ with $\pm$. So, the method only works separately for the upper and lower halves of the circle. This is where parametric curves come handy.
Define $$g(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t), t\in[ 0, \frac{\pi}{4} ].$$
In addition to "In what direction?" we also consider "How fast?" (it's already clear that one can give one answer to both questions - in the form of a vector). Suppose it's released at time $t = \frac{\pi}{4}$. What is the velocity, with respect to $x$ and $y$, of the motion?
- $x(t) = {\rm cos \hspace{3pt}} t {\rightarrow} x'(t) = -{\rm sin \hspace{3pt}} t {\rightarrow} x'(\frac{\pi}{4}) = -\frac{1}{\sqrt{2}},$
- $y(t) = {\rm sin \hspace{3pt}} t {\rightarrow} y'(t) = {\rm cos \hspace{3pt}} t {\rightarrow} y'(\frac{\pi}{4}) = \frac{1}{\sqrt{2}}.$
Then the answer is the velocity: $v = ( -\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}).$
Further, if the rock is released, it will continue with this velocity indefinitely: $$s(t) = ( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}) + v( t - \frac{\pi}{4}), t \in [ \frac{\pi}{4}, \infty ),$$ where $( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ indicates the initial position, $v$ the velocity and $\frac{\pi}{4}$ the time since the release. This yields a straight line.
In the $n$-dimensional space, such a geometric approach is no longer valid. We have to take a more algebraic view.
Recall from Calc 1:
- Question: Given $y = f(x)$, what is the best linear approximation of $f$ around $x = a$?
- Answer: The tangent line, $g(x) = f(a) + f'(a) ( x - a ).$
Now we realize that the right term here is affine not linear.
Problem. Give the set of all affine functions passing through $(a,f(a))$ $$g(x) = f(a) + m ( x - a ).$$ which one is he best approximation of $f$ around $x = a$?
We know the answer: $m = f'(x).$
It's best but in what sense?
Let's rephrase the problem in the vector environment.
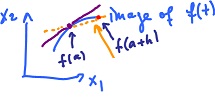
Let $f: {\bf R} {\rightarrow} {\bf R}^n, a \in {\bf R}$. What is the rate of change of $f$? We have
- $z:$ Change $f(a + h) - f(a) - f(a)$ a vector, the displacement
- $t$: Change $h$ a number, the time passed
Then the rate of change of $z$ with respect to $t$ can be expressed as $$\frac{f(a + h) - f(a)}{h}.$$ This is a vector. The instant rate of change is $$f'(a) = \displaystyle\lim_{h \rightarrow 0} \frac{f(a + h) - f(a)}{h}.$$ Also a vector.
How can we compute this? Suppose $f(t) = ( f_1(t), f_2(t), ..., f_n(t) )$, then $$\begin{array}{} f'(a) &= \displaystyle\lim_{h \rightarrow 0} \frac{\left( f_1(a + h), ..., f_n(a + h) ) - ( f_1(a), ..., f_n(a) \right)}{h} \\ &= \left( \displaystyle\lim_{h \rightarrow 0} \frac{f_1(a + h) - f_1(a) )}{h}, ..., \displaystyle\lim_{h \rightarrow 0} \frac{f_n(a + h) - f_n(a)}{h} \right) \\ &= ( f'_1(a), ..., f'_n(a) ). \end{array}$$
Theorem. The derivative $f'(a)$ exists iff $f'_i(a)$ exists for all $i = 1, ..., n$. Also $f'(a) = ( f'_1(a), ..., f'_n(a) )$.
Definition. Given $f: {\bf R} {\rightarrow} {\bf R}^n, a \in {\bf R}$, an affine function $k: {\bf R} {\rightarrow} {\bf R}^n$ is the best affine approximation of $f$ at $x = a$ if
- $k(a) = f(a)$,
- $\displaystyle\lim_{t \rightarrow a} \frac{f(t) - h(t)}{t - a} = 0.$
The last condition encodes the idea of approximation: not only the difference between $f$ and its approximation is "small" but it's small even relative to the change in the input, $t - a$.
The theorem below justifies "the" in the definition.
Proposition. The best affine approximation is unique.
Proof Let $k_1, k_2$ satisfy (1) and (2). Then
- $k_1(t) = f(a) + v_1(t - a)$
- $k_2(t) = f(a) + v_2(t - a)$.
Apply algebra along with (2) to conclude the proof.
Suppose $k(t) = f(a) + v( t - a )$ is the best affine approximation. Then $v$ is called the derivative of $f$ at $a$, so that $k(t) = f(a) + f'(a) ( t - a ).$
Example 2. $f(t) = ({\rm cos \hspace{3pt}} 5t, {\rm sin \hspace{3pt}} 5t)$, then $f'(t) = 5 (-{\rm sin \hspace{3pt}} 5t, {\rm cos \hspace{3pt}} 5t)$ and $|| f'(t) || = 5$. Constant speed!
Example 3. Let $f(t) = ({\rm cos \hspace{3pt}} t^2, {\rm sin \hspace{3pt}} t^2)$, then
$$\begin{array}{} f'(t) &= (-{\rm sin \hspace{3pt}} t^2 2t, {\rm cos \hspace{3pt}} t^2 2t) \\ &= 2t (-{\rm sin \hspace{3pt}} t^2, {\rm cos \hspace{3pt}} t^2). \end{array}$$
Further $|| f'(t) || = 2t$ as
$$|| (-{\rm sin \hspace{3pt}} t^2, {\rm cos \hspace{3pt}} t^2) || = 1. $$
The speed $|| f'(t) ||$ is not constant this time.
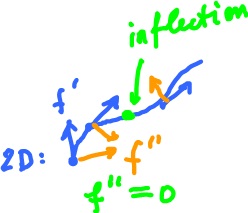
Recall however $< f, f' > = 0$, so $f \perp f'$, and $< f', f′′> = 0$ if $|| f'(t) ||$ is constant.
The speed is perpendicular to the acceleration.
Algebraic properties of the derivative
In this section we'll see how the derivative is affected by vector operations.
Addition and multiplication behave the exact same way as in dimension $1$, but there is no division...
Consider $f,g: {\bf R} {\rightarrow} {\bf R}^n$ and they have derivatives at a point $x = a$.
$$(f + g)' = f' + g'.$$
Proof. Coordinate-wise.
Scalar product rule.
$$(\alpha f)' = \alpha \cdot f'.$$
Same proof as above.
Dot product rule.
$$<f, g>' = <f', g> + <f, g'>.$$
Proof. $$\begin{array}{} &= (f_1 g_1, f_2 g_2, f_n g_n)', {\rm \hspace{3pt} where \hspace{3pt}} f_i, g_i: {\bf R} {\rightarrow} {\bf R} \\ &= (f'_1 g_1 + f_1 g'_1) + ... + (f'_n g_n + f_n g'_n) \\ &= (f'_1 g_1 + f'_2 g_2 + ... + f'_n g_n) + (f_1 g'_1 + f_2 g'_2 + ... + f_n g'_n) \\ &= <f', g> + <f, g'> \end{array}$$
Cross product rule.
$$(f \times g)' = f' \times g + f \times g', (n = 3)$$
What about the norm $||f||$?
$$\begin{array}{} (||f||^2)' &= (<f, f>)' \\ &= <f', f> + <f, f'> \\ &= 2 <f', f>. \end{array}$$
Example. Consider rotation again. This means that we assume that $|| f ||$ constant, where $f$ is the location. Then $|| f ||^2$ = constant, differentiate the equation. $( (|| f ||)^2 )′ = 0$, so $2< f', f' > = 0$, thus $< f', f > = 0$. Hence
$$f' \perp f.$$
Example. What if the speed is constant? What is acceleration then? Let $g$ denote location, $g'$ velocity, $|| g' ||$ the speed. Using the previous example with $f = g'$, we obtain
$$f ⊥ f'$$
or, in our notation,
$$g' ⊥ g' '.$$
Chain Rule. Let $f: {\bf R} {\rightarrow} {\bf R}^n, g: {\bf R} {\rightarrow} {\bf R}$, then $fg: {\bf R} {\rightarrow} {\bf R}^n$ if domain $g \supset$ range $f$.
If $f'$ and $g'$ exist, then
$$(f \circ g)' = f' \circ g \cdot g'.$$
Vector fields
Where do parametric curve come from? One source is vector fields.
Let us consider a few examples of vector fields in dim $2$.
Problem. Given directions (and magnitudes) everywhere, we are interested in finding the paths, i.e., parametric curves, of particles like water that follow these directions.
Consider a vector field $F: {\bf R}^n {\rightarrow} {\bf R}^n$, where $F$ plots points onto vectors. We want to find a path $f: {\bf R} {\rightarrow} {\bf R}^n$, satisfying
$$f'(t) = F( f(t) ),$$
where $f'$ denotes the velocity, $F$ a vector, and $f(t)$ a point.
Note that we can think of this problem as an ordinary differential equation: $$x' = F(x).$$
Example. The simplest example is one with $F(X) = u$ constant vector. If $f'(t) = u$, solve (through integration) as
$$f(t) = t ⋅ u + C, $$
where $t$ denotes time and $C$ the initial position $f(0)$,
$$f(0) = C.$$
The answer is an affine function.
Example. Rotation:
- $f'(t) = ( {\rm sin \hspace{3pt}} t, {\rm cos \hspace{3pt}} t)$ or
- $( f'_1(t), f'_2(t) ) = ( {\rm sin \hspace{3pt}} t, {\rm cos \hspace{3pt}} t)$ or
- $f'_1(t) = {\rm sin \hspace{3pt}} t, f'_2(t) = {\rm cos \hspace{3pt}} t.$
Solve $$f_1(t) = - {\rm cos \hspace{3pt}} t + C_1, f_2(t) = {\rm sin \hspace{3pt}} t + C_2.$$
So
$$f(t) = ( -{\rm cos \hspace{3pt}} t + C_1, {\rm sin \hspace{3pt}} t + C_2 ) = ( -{\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t) + C$$
We applied coordinate-wise anti-differentiation to get $f: {\bf R} {\rightarrow} {\bf R}^n.$
Exercise. Plot $f'$ and then a few paths.
Lengths as integrals
To define integrals properly we need some background.
Definition. Given a set of real numbers $S$, an upper bound $n$ of $S$ is a number $n < \infty$ or $\infty$, such that
Example.
- If $S = [0 , 1]$, what are the upper bounds? The upper bounds are $1, 2, 3, {\pi}, \infty$, etc.
- If $S = (0 , 1]$, the upper bounds are the same as above.
- If $S = \{1, 2, 3, 4, ... \}$, the only upper bound is $\infty$.
- If $S = \{\frac{1}{n}, n = 1, 2, 3, ... \}$, then $1$ is an (especially good) upper bound.
Definition. The least upper bound is the smallest of all the upper bounds of $S$.
Theorem. The least upper bound always exists.
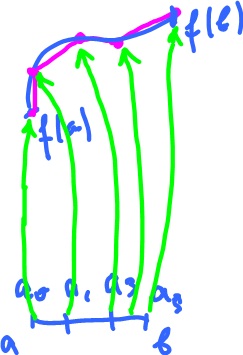
Let $f$ be a parametric curve
$$f : {\bf R} {\rightarrow} {\bf R}^n $$
and $b > a$. Define the length of the curve from $f(a)$ to $f(b)$.
We "approximate" the curve with segments. Pick $s$ points $A_1, A_2, ..., A_s$ on the curve with $A_i = f( a_i), a_i < a_{i+1}$ (note that this is a partition of the interval).
The length of segment $[A_i, A_{i+1}]$ is $$||A_i - A_{i+1}||.$$ Then the total length is
$$L({A_i}) \leq \displaystyle\sum_{i=1}^s||A_i - A_{i+1}||.$$
Suppose the "true" length is equal to $l$. Then $L \leq l.$
Review exercises.
(1) Suppose for $f,g: {\bf R} {\rightarrow} {\bf R}^q, < f, g >$ continuous. Does it mean that $f$ and $g$ are continuous?
No. As a counterexample consider $f,g: {\bf R} {\rightarrow} {\bf R}$ with $f = 0$. Then $f ⋅ g = 0$. But $g$ can be anything!
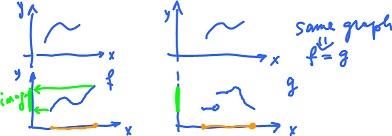
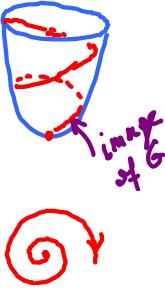
(2) Suppose $f$ is continuous and image $f$ = image $g$, does it mean that $g$ continuous too?
No. See the illustration. Note that
but this question is about the image.
(3) Find the angle of intersection of two curves:
$$({\rm cos \hspace{3pt}} t, 3 {\rm sin \hspace{3pt}} t) {\rm \hspace{3pt} and \hspace{3pt}} (2 {\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t).$$
We need to solve the equation:
$$({\rm cos \hspace{3pt}} s, 3 {\rm sin \hspace{3pt}} s) = (2 {\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t)$$
with different parameters! This vector equation turns into two regular equations:
$${\rm cos \hspace{3pt}} s = 2 {\rm cos \hspace{3pt}} t,$$
$$3 {\rm sin \hspace{3pt}} s = {\rm sin \hspace{3pt}} t,$$
from which we want to find $s$ and $t$. Then
$$1 = {\rm cos \hspace{3pt}}^2 t + {\rm sin \hspace{3pt}}^2 t = (1 / 2 {\rm cos \hspace{3pt}} s)^2 + (3 {\rm sin \hspace{3pt}} s)^2.$$
Now solve for $s$, then find $t$. Compute the derivatives of these two functions for those values of $s$ and $t$. Find the angle by means of the dot product.
Definition. Define the length as the least upper bound of
$$L({ A_i }). $$
Consider the length of a curve $f: [a, b] {\rightarrow} {\bf R}^n$. By theorem, the length always exists. If the length is finite,
$$L( f; [a, b] ) \neq \infty, $$
then $f$ is called rectifiable. Thus number is also called the arc length.
Theorem. Suppose $f: [a, b] {\rightarrow} {\bf R}^n$ is rectifiable and $\gamma: [c, d] {\rightarrow} [a, b]$ is monotone and continuous. Then
$$g = f \gamma: [c, d] {\rightarrow} {\bf R}^n$$
is rectifiable, and $L( f; [a, b] ) = L ( g; [c, d] ).$
This theorem is about a re-parametrization of the curve.
$L( f; [a, b] )$ is approximated by sum discussed above:
$$L({ A_i }) = \displaystyle\sum_{i=0}^{n-1} || f(a_{i+1}) - f(a_i) ||.$$
The idea is to turn this into an integral
$$\displaystyle\int_a^b h(x) dx.$$
As usual, this is done by recognizing the Riemann sum of some function, $h$:
$$\displaystyle\sum_{i=0}^{n-1} h(a_i) \Delta x, {\rm \hspace{3pt} where \hspace{3pt}} \Delta x = a_{i+1} - a_i.$$
To get to this point we re-write the sum
$$L({ A_i }) = \displaystyle\sum_{i=0}^{n-1} || f(a_{i+1}) - f(a_i) || \frac{\Delta x}{\Delta x}$$
to make
$$|| f(a_{i+1}) - f(a_i) || \frac{1}{\Delta x} = h(a_i).$$
Further
$$L({ A_i }) = \displaystyle\sum_{i=0}^{n-1} || f(a_{i+1}) - f(a_i) || / (a_{i+1} - a_i) \Delta x,$$
so that
$$\frac{|| f(a_{i+1}) - f(a_i) ||}{(a_{i+1} - a_i)} \rightarrow || f'(x) ||.$$
The limit is
$$L( f; [a, b] ) = \displaystyle\int_a^b || f'(x) || dx.$$
Example. The length of a circle of radius $r$ is equal to $2{\pi}r$. How do we know? Describe the circle as
$$f(t) = r ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t), t \in [0, 2{\pi}].$$
Now
$$f'(t) = r ( -{\rm sin \hspace{3pt}} t, {\rm cos \hspace{3pt}} t)$$
and
$$|| f'(t) || = r ({\rm {\rm sin \hspace{3pt}}}^2 t + {\rm cos \hspace{3pt}}^2 t)^{\frac{1}{2}} = r.$$
Then $$L = \displaystyle\int_0^{2 \pi} r dt = rt |_0^{2 \pi} = r (2{\pi} - 0) = 2{\pi}r.$$
Re-parametrization
Example. Let $g$ parametrize a circle with
$$g(t) = r({\rm cos \hspace{3pt}} (-t), {\rm sin \hspace{3pt}} (-t)), {\rm \hspace{3pt} and \hspace{3pt}} \gamma(t) = -t.$$
Then $|| g'(t) || = 1,$ i.e. by the formula the curve has the same length. Further, what about
$$g(t) = r ({\rm cos \hspace{3pt}} ({\pi} + t), {\rm sin \hspace{3pt}} ({\pi} + t)), \gamma (t) = {\pi} + 3?$$
Substituting for $\gamma = 3t$ yields
$$g(t) = r ({\rm cos \hspace{3pt}} 3t, {\rm sin \hspace{3pt}} 3t), {\rm \hspace{3pt} where \hspace{3pt}} t \in [0, 2{\pi} / 3]$$
and
$$|| g'(t) || = r \cdot 3.$$
Then
$$L = \displaystyle\int_0^{\frac{2 {\pi}}{3}} 3r dt = \frac{6}{3} {\pi}r = 2{\pi}r.$$
A variety of parametrizations will produce the same result.
Is there a special one or the best one?
What if we follow the curve with the speed be equal to $1$? This is indeed special and there are only two ways to do that. So, if $|| f' || = 1$ for all $t$, this is called the natural parametrization of the curve.
Example. What is the natural parametrization of the circle? The "standard" parametrization
$$g(t) = r ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t)$$
is not natural because $|| g'(t) || = r.$
Consider $\gamma(t) = \frac{t}{r}$, then
$$f(t) = r ({\rm cos \hspace{3pt}} \frac{t}{r}, {\rm sin \hspace{3pt}} \frac{t}{r})$$
and $|| f'(t) || = r \cdot \frac{1}{r} = 1$ since $\gamma'(t) = \frac{1}{r}$.
Observe that if $f$ is the natural parametrization, then
$$L( f; [0, t] ) = t.$$
Let $g: {\bf R} {\rightarrow} {\bf R}^n$ be a curve with natural parametrization, and let $f: {\bf R} {\rightarrow} {\bf R}^n$ denote another parametrization of the same curve. Then $g = f \gamma$, where $\gamma: {\bf R} {\rightarrow} {\bf R}$ is increasing.
The Chain Rule above yields $g'({\tau}) = f'( {\gamma}({\tau}) ) \cdot {\gamma}'({\tau})$ (note that ${\gamma}'({\tau})$ is a number here)
and
$$\begin{array}{} 1 &= || g'({\tau}) || \\ &= || f'( {\gamma}({\tau}) ) \cdot {\gamma}'({\tau}) || \\ &= || f'( {\gamma}({\tau}) ) || \cdot | {\gamma}'({\tau}) | \\ &= || f'( {\gamma}({\tau}) ) || \cdot {\gamma}'({\tau}). \end{array}$$
Then ${\gamma}'({\tau}) = \frac{1}{|| f'( {\gamma}({\tau}) ) ||}$ (re-parametrization).
Example. Consider a helix
$$f(t) = ({\rm cos \hspace{3pt}} t, {\rm sin \hspace{3pt}} t, t).$$
Then $f'(t) = ( -{\rm sin \hspace{3pt}} t, {\rm cos \hspace{3pt}} t, 1)$ and $|| f'(t) || = ( (-{\rm sin \hspace{3pt}} t)^2 + ({\rm cos \hspace{3pt}} t)^2 + 1^2 )^{\frac{1}{2}} = \sqrt{2}.$ Then
$${\gamma}'({\tau}) = \frac{1}{\sqrt{2}}, {\rm \hspace{3pt} hence \hspace{3pt}} {\gamma}({\tau}) = \frac{1}{\sqrt{2}} \cdot {\tau}.$$
Define
$$g({\tau}) = f( {\gamma}({\tau}) ) = \left( {\rm cos \hspace{3pt}} \frac{\tau}{\sqrt{2}}, {\rm sin \hspace{3pt}} \frac{\tau}{\sqrt{2}}, \frac{\tau}{\sqrt{2}} \right).$$
This is the natural parametrization and {\tau} is called the natural parameter.
Review exercise. Plot the curve:
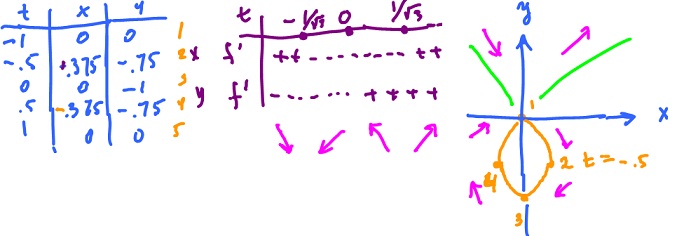
$$F(t) = ( t (t^2 - 1), t^2 - 1 )$$
$$F'(t) = ( 3t^2 - 1, 2t ), t = \pm \frac{1}{\sqrt{3}}, 0$$
Record the values of $F$ and $F'$ for a few values of $t$ in the table, then plot the curve:
Curvature
Let us first consider the circle again:
$$g(t) = ( r {\rm cos \hspace{3pt}} \frac{t}{r}, r {\rm sin \hspace{3pt}} \frac{t}{r} )$$
with radius $r$. Then the tightness of the turn, the curvature, is the reciprocal of the radius:
$$\kappa = \frac{1}{r}.$$
Definition. The curvature of the curve $z = g(t)$, where $t$ is the natural parameter, at $f(t)$ is defined by
$$\kappa = || g' '(t) ||.$$
It's like the strength of the $g$-force that you have to deal with when turn...
Example. Circle: $$g'(t) = ( -{\rm sin \hspace{3pt}} \frac{t}{r}, {\rm cos \hspace{3pt}} \frac{t}{r} ),$$
$$g' '(t) = ( - \frac{1}{r} {\rm cos \hspace{3pt}} \frac{t}{r}, - \frac{1}{r} {\rm sin \hspace{3pt}} \frac{t}{r} ).$$
$$\kappa = || g' '(t) || = \frac{1}{r} || ( {\rm cos \hspace{3pt}} \frac{t}{r}, {\rm sin \hspace{3pt}} \frac{t}{r} ) || = \frac{1}{r}.$$
Example. Helix:
$$g(t) = ( {\rm cos \hspace{3pt}} \frac{t}{\sqrt{2}}, {\rm sin \hspace{3pt}} \frac{t}{\sqrt{2}}, \frac{t}{\sqrt{2}}) {\rm \hspace{3pt} (natural \hspace{3pt}} parameter)$$
Then
$$g'(t) = ( -\frac{1}{\sqrt{2}} {\rm sin \hspace{3pt}} \frac{t}{\sqrt{2}}, \frac{1}{\sqrt{2}} {\rm cos \hspace{3pt}} \frac{t}{\sqrt{2}}, \frac{1}{\sqrt{2}})$$
$$g' '(t) = ( -\frac{1}{2} {\rm cos \hspace{3pt}} \frac{t}{\sqrt{2}}, -\frac{1}{2} {\rm sin \hspace{3pt}} \frac{t}{\sqrt{2}}, 0)$$
and
$$\kappa = || g' '(t) || = \frac{1}{2} || ( {\rm cos \hspace{3pt}} \frac{t}{\sqrt{2}}, {\rm sin \hspace{3pt}} \frac{t}{\sqrt{2}} ) || = \frac{1}{2}.$$
We define the radius of curvature as $\frac{1}{\kappa}$.
- Helix: $\frac{1}{\kappa} = 2$, radius $= 1$.
- Circle: $\frac{1}{\kappa} = 1$, radius $= 1$.
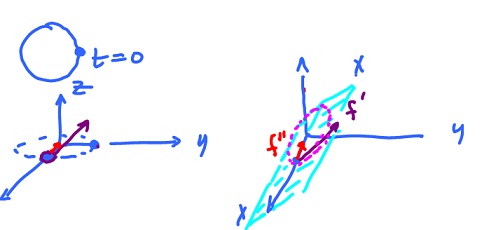
The osculating circle approximates the curve at the point and has radius equal to $\frac{1}{\kappa}$. This way the curvature of the circle is the same as that of the curve. The circle is located in the osculating plane determined by $g'$ and $g' '$, below.
Compare:
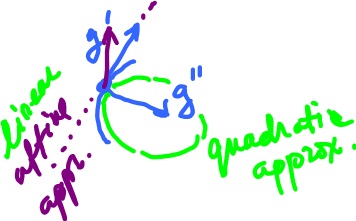
- $y = mx + b$ the best affine approximation, linear polynomial;
- $ax^2 + bx + c$, quadratic polynomial.
How do we find the osculating circle? Consider $f(t)$ at $t = a$, with $t$ the natural parameter. Compute $\kappa$, $R = \frac{1}{\chi}$.
The center of the circle is $f(a) + R \frac{f' '(a)}{|| f' '(a) ||}= f(a) + \frac{1}{\kappa^2} f' '(a).$
Example. Let us consider a helix, $a = 0, \kappa = 1 / 2, R = 2.$
Here
- $f(0) = ( 1, 0, 0 ),$
- $f'(0) = ( 0, \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}),$
- $f' '(0) = ( -\frac{1}{2}, 0, 0).$
What if t is not natural? Then we can plot $g(\tau) {\rightarrow} f( \gamma(\tau) ),$ and we know $\gamma$. Then the formula is
$$\kappa = \frac{||f'|| f' ' - < f', f' ' > f'}{||f'||^4}.$$
Example. Consider the curve $G(s) = ( s {\rm cos \hspace{3pt}} s, s {\rm sin \hspace{3pt}} s, s^2 + 1 )$ on the surface
$$x^2 + y^2 = z - 1.$$
This is another way of representing the curve:
$$x = s {\rm cos \hspace{3pt}} s, y = s {\rm sin \hspace{3pt}} s, z = s^2 + 1.$$
These $x, y, z$ have to satisfy the equation
$$( s {\rm cos \hspace{3pt}} s^2) + ( s {\rm sin \hspace{3pt}} s)^2 = ( s^2 + 1 ) - 1$$
or
$$s^2 {\rm cos}^2 s + s^2 {\rm sin}^2 s = s^2.$$
Now one can see from the Pythagorean Theorem that the equation
$$s^2 ( {\rm cos \hspace{3pt}}^2 s + {\rm sin \hspace{3pt}}^2 s) = s^2$$
holds.
Review exercise. (1) Consider a ray from $( 0, 1, 0, 1)$ through $( 1, 0, 1, 0)$.
Write $f(t) = tu + P, t \geq 0$, where
- $u$: vector direction
- $P$: the initial point $f(0) = P$.
Let $P = ( 0, 1, 0, 1)$. What is $u$? Define point $Q$ as $Q = ( 1, 0, 1, 0)$, then
$$\begin{array}{} u &= Q - P \\ &= ( 1, 0, 1, 0) - ( 0, 1, 0, 1) \\ &= ( 1, -1, 1, -1). \end{array}$$
Then the specific parametrization of the line is
$$f(t) = t ( 1, -1, 1, -1) + ( 0, 1, 0, 1), t \geq 0.$$
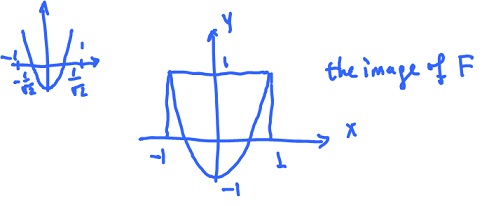
(2) Consider $F(t) = ( {\rm cos \hspace{3pt}} t, {\rm cos \hspace{3pt}} 2t), 0 \leq t \leq {\pi}$
What is the image of $F$? Let $x = {\rm cos \hspace{3pt}} t$ and $y = {\rm cos \hspace{3pt}} 2t = 2 {\rm cos \hspace{3pt}}^2 t - 1 = 2x^2 - 1$ (parabola). Then
$$x, y \in [ -1, 1].$$
For more see Parametric curves: exercises.