Quotient sets

The easiest way to construct the circle $S^1$ is to take segment $[0,1]$ and glue the end points together.

The gluing procedure is captured by the following equivalence relation on $X = [0,1]$:

• (1) $x \sim x$ for all $x$,
• (2) $0 \sim 1$.

The first part is required by the definition of equivalence relation and does not have to be repeated. Then $$S^1 = [0,1]/_{\sim},$$ i.e., the set of equivalence classes: $$X / _{\sim} = \{[x]: x∈X\} = \{ {0,1} \} \cup \{ {x}: x∈(0,1) \}.$$

Definition. Given a set $X$ and an equivalence relation $~$ on it, the corresponding quotient set $X/_{\sim}$ is the set of its equivalence classes: $$X / _{\sim} = \{[x]: x∈X\}.$$

In the next example, let

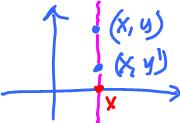
• $X = R^2$ and
• $(x,y) \sim (x,y')$ for all $x,y$.

Then the equivalence classes are the vertical lines. Instead of using the "gluing" metaphor, we say here that each of these lines collapses to a point. Indeed each of the vertical lines corresponds to its point of intersection with the $x$-axis. Hence, the quotient space is the real line. Algebraically, $$X/_{\sim} = \{ \{(x,y): y∈R\} : x∈R\} = \{ x : x∈R\} = R.$$

The function that takes each point to its equivalence class is called the quotient function

• $q: X → X/_{\sim}$ given by
• $q(x) = [x]$.

In the second example $q$ is the projection:

• $q: R^2 → R$ given by
• $q(x,y) = x$.

In the first example the quotient map $$f: [0,1] → S^1$$ is given by $$f(t) = (cos(πt), sin(πt))$$ for $t∈[0,1]$.

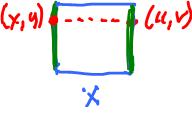
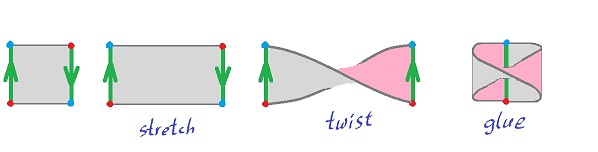
One can glue the two opposite edges of the square to create a cylinder. Here $$X = [0,1] \times [0,1] = \{(x,y): x∈[0,1], y∈[0,1]\}.$$ And the equivalence relation is given by

• $(x,y) \sim (u,v)$ if $y=v$ and $x,u=0$ or $1$,

or simply

• $(0,y) \sim (1,y)$.

The green arrows in the image above indicate how the two edges are attached to each other. If you reverse the orientation, you will get the Mobius band $M$:

The equivalence relation is given by

• $ (x,y) \sim (u,v)$ if $y=1-v$ and $x,u=0$ or $1$,

or simply

• $ (0,y) \sim (1,1-y)$.

For more examples of this, topological, kind see Quotient spaces.

A special kind of a quotient space is when a subset is collapsed to a single point. Given $X$ and a subset $A$, the equivalence relation is defined by:

• $x \sim y$ for all $x,y∈A$.

Then we use the notation: $$X/A,$$ read "$X$ mod $A$".

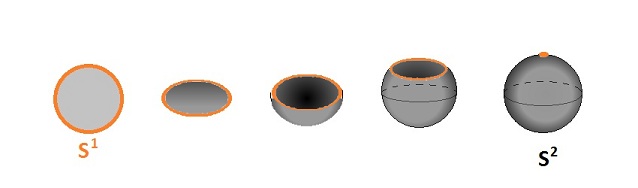
For example, one can construct the sphere $S^2$ by from the disk $D^2$ by collapsing its boundary to a point: $$S^2 = D^2 /S^1 .$$ The construction is illustrated below:

For algebraic examples, see Quotients of vector spaces.