This site is being phased out.
Measure vegetation coverage
Developing a Pixcavator protocol for estimating the area covered by plant material per square
Q. From these images "we want to derive the area of the board covered by plant material to serve as an index of plant density." We would like to "develop .. a simple protocol for estimating area-covered by plant material in our digital images with Pixcavator. "
This would be hard to accomplish with images similar to these. To capture the vegetation effectively, one has to separate it from the background. Then, ideally, the latter would have to either uniformly lighter or uniformly darker than the former (see Gray scale images). The light/dark squares make the task very challenging.
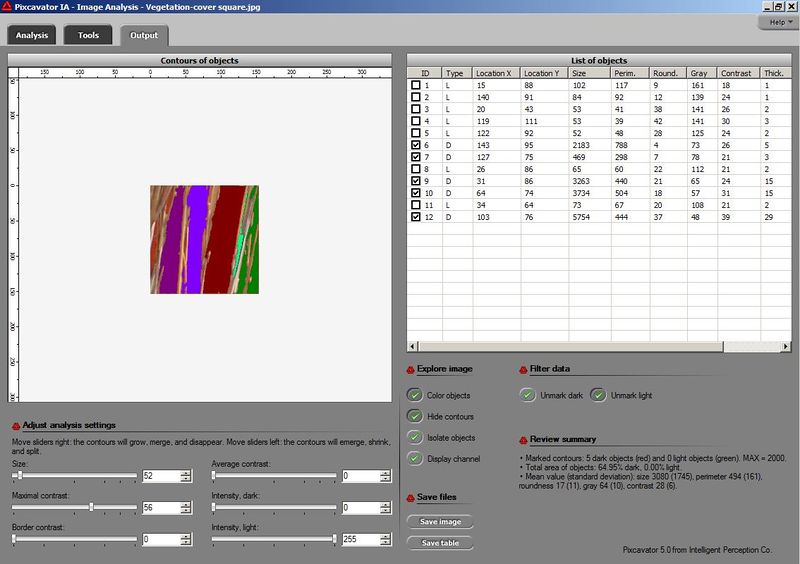
Instead, one can digitally isolate the squares within each image, so that the area covered by vegetation can be estimated from a set of sub-images (i.e., individual squares) with uniform background colors:
In the screenshot, the colored areas are the complement of the vegetation. Their total area is 64.95%, so the vegetation takes the rest, 35.05%.
Another approach is to replace the red throughout the image with something else. I tried that in the image attached but was only half successful. Somehow the red was replaced with gray not white. In this case, the vegetation is darker than the white squares but lighter than the gray squares. This creates edges and the computations become meaningless. However, I didn't really give this approach a lot of time. It is still possible that it could work. If it does, then there would be much less work than the alternative: cutting out the squares, saving them in separate files, then processing each. One correctly chosen color replacement can be repeated in all images...
Q. "Do you think any particular [single] color would better facilitate image analysis with Pixcavator?"
The goal is provide as much contrast as possible between what we want to capture and the background. Taking into account the color of the vegetation to be captured would be especially smart approach. If this is unpredictable then white and black are the two main possibilities.
Blue gives a good separation of the background. The main problem is to know where the bottom of the board is. One way is to use marks on the board that will convey its size and orientation to the computer. Some kind of calibrating markings on the board could make it possible to automate the part of the processing finding the board in the image.
I think the board should be white on one side and black on the other. Here's why. The color of the vegetation and the lighting conditions can vary. As a result, sometimes the vegetation may look somewhat light or somewhat dark. In the former case you want to put it on the dark background and in the latter on the light background, for better contrast. Then it makes sense to choose black and white because black is darker than any color and white is lighter than any color. Even though it is unlikely that the vegetation would be blue, black and white combination is the simplest solution.
In the image example, the blue board was darker than the green vegetation (under the green color channel). That created the necessary contrast to distinguish them. But the contrast of green with black would be even more pronounced. Certainly, there may be issues such as what white be like under direct sunlight or what if white gets scratched or dirtied in the field (spray paint should help). And digital imaging may produce colors different from reality. It's hard to know without testing.
There are a couple of issues unrelated to colors.
First, I didn't know where the bottom of the board was so I just guessed. This problem is easy to solve by selecting a board that is a square. (A square board would also ensure that one wouldn't put it on the wrong side - in the field - and mess up the computations as a result.)
Second, the board is a bit askew. So, instead of square/rectangle we have a parallelogram. A way to solve this is either to align the camera with the board somehow or deal with the image later, e.g. manually erasing the parts that stick out from the rectangle.
Third, if we know the proportions of the board, markings won't be necessary. Some marks may still be needed for proper alignment of the board if, for example, the top isn't horizontal with respect to the photo or if the photo is taken under an angle (off-center) turning the image of the board into a parallelogram. (It is my feeling that whatever issues you have in the field, they are easier to handle digitally, in the comfort of your office.)
Height and volume of vegetation
The area covered should be just a step towards what we are really interested in - the height of the vegetation (or volume, even better).
Let's consider how one can compute the height of vegetation from a digital image. The idea is very simple:
the average height = the area / the width.
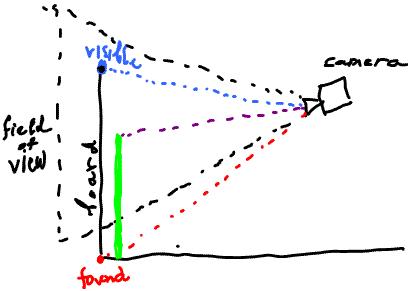
Consider now what we see in the image.
Views from a side (vegetation in green) and from above:
Assumptions:
- The board is a square and its dimensions are known.
- The board is vertical (otherwise it's impossible to know where the bottom is).
- The bottom of the board is horizontal on the horizontal (along the board) ground.
- The field of view of the camera includes the edge of the vegetation and the top of the board.
Then, the average height computed as below is independent from:
- the deviation of the angle of the camera from the horizontal,
- the distance from the camera to the board,
- the height of the position of the camera above the ground.
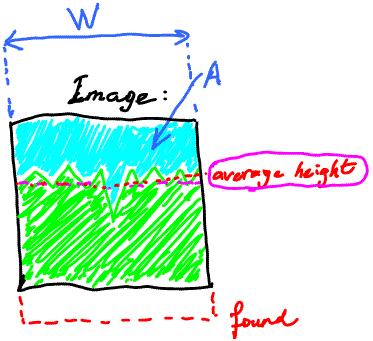
The measurements (the image in black, the bottom of the board in red):
These come from image analysis:
A = the area of the board visible above the vegetation (sq pixel), W = the width of the board (pixel).
This is known:
S = the length of the side of the board (in), which is assumed to be a square.
The average distance from the top of the board to the edge of the vegetation (pixel):
H0 = A / W.
The conversion factor (in/pixel) - can be found in a number of other ways:
C = S / W.
The average distance from the top of the board to the edge of the vegetation (in):
H1 = H0*C.
Average height of the vegetation above the ground (in):
H = S - H1.
Simplified:
H = S - H0 * S / W
= S - (A / W) * (S / W)
= S* (1 - A / W2).
Computing the average height interesting because, when combined with the shots from above (see Measuring seedling area), one can use it to evaluate the volume of the vegetation. Still to come...