This site is being phased out.
Integer-valued calculus
God made the integers, all else is the work of man. -- Leopold Kronecker
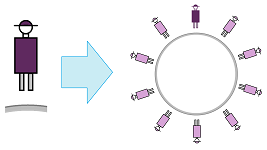
First question: does the universe have a hole (or tunnel) in it? Is it possible to travel in a straight line and arrive at the starting point from the opposite direction? Like this:
Second question: is the universe orientable? Can one go on a trip and then come back as a mirror image of himself? Including the internal organs, like this:
Since we can't step outside the universe and take a look, these questions are about intrinsic, topological properties of our universe.
Can calculus, as we know it, help to answer these two questions?
Let's start at a simple place, Calculus 3, dimension $2$: all vector fields on a plane region with a zero rotor (aka curl) are gradient -- provided the region is simply-connected. So, if we know all gradients of all functions and all line integrals of all vector fields, we can tell if there is a hole in the region. Thus, we can say that calculus on the plane is different from calculus on the punctured plane.
Let's look at the details... Consider a “rotation” vector field: $$V=<y,\ -x>,$$ and then its multiple defined on the punctured plane: $$F=\frac{V}{||V||^2}=\frac{1}{x^2+y^2}<y,\ -x>=\left< \frac{y}{x^2+y^2},\ -\frac{x}{x^2+y^2}\right>=<p,q>.$$
We compute the rotor of the latter first: $$\operatorname{rot}F=q_x-p_y=0.$$ The vector field is, therefore, irrotational. Next, suppose $C$ is the unit circle and $X=X(t)$ is its counterclockwise parametrization. Then $F(X(t))$ is parallel to $X'(t)$. Therefore, $F(X(t))\cdot X'(t)>0$. It follows that the line integral along the circle is positive: $$0=\oint_C F\cdot dX=\int_a^b F(X(t))\cdot X'(t)\, dt>0.$$ On the other hand, the line integral over a closed path of a gradient vector field would be $0$ according to the Fundamental Theorem of Calculus for gradient vector fields. A contradiction!
Because there is a hole in the space, there is a vector field that is irrotational but not gradient. And vice versa!
This point is easier to make if we switch to manifolds...
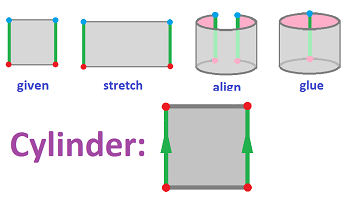
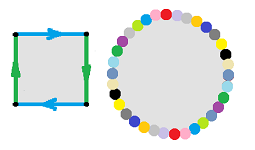
As an example, the analog of the punctured plane is the cylinder. We make it from the square by gluing together two of its opposite edges:
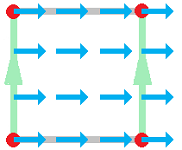
Consider a constant horizontal vector field defined on the cylinder: $$F=<p,q>=<1,0>.$$
We go through the same steps now. Compute the rotor first: $$\operatorname{rot}F=q_x-p_y=0.$$ The vector field is irrotational. Next, suppose $C$, parametrized by $X=X(t)$, is a path along the top edge of the cylinder. Then $F(X(t))$ is parallel to $X'(t)$. Therefore, $F(X(t))\cdot X'(t)>0$. It follows that the line integral along the circle is positive: $$0=\oint_C F\cdot dX=\int_a^b F(X(t))\cdot X'(t)\, dt>0.$$ On the other hand, the line integral over a closed path of a gradient vector field would be $0$ according to the Fundamental Theorem of Calculus for gradient vector fields on manifolds. A contradiction! Therefore, we have a vector field that is irrotational but not gradient.
Now we recast this construction in the language of differential forms.
Differential forms come from the integral theorems of $2$-dimensional calculus. First, Green's Theorem: $$\oint_C F\cdot dX=\iint_D \operatorname{rot}F\, dxdy,$$ where a loop $C$ is the boundary of a region $D$, $$\partial D=C.$$ Here, the integrand of the line integral on the left is a form of degree $1$ (with $X=<x,y>,\ dX=<dx,dy>$), while the integrand of the area integral on the right is a form of degree $2$: $$\phi=F\cdot dX\ \text{ and } \Psi=\operatorname{rot}F\, dxdy.$$ The latter is called the exterior derivative of the former: $$d\phi=\Psi.$$ In the particular case of the cylinder, the latter form is $0$. And the form $\phi$ is called closed.
Second, the Fundamental Theorem of Calculus of line integrals states: $$f(B)-f(A)=\int_C \operatorname{grad} f\cdot dX,$$ where $C$ is a path from $A$ to $B$, i.e., $$\partial C=B-A.$$ Every function $f$ on the plane is a form of degree $0$ and its exterior derivative $df$ is a form of degree $1$. This new form is given by the gradient of $f$: $$\phi=df=\operatorname{grad} f\cdot dX.$$ In the particular case of the cylinder, there is always such an $f$. And the form $\phi$ is called exact.
So, calculus on the plane is different from calculus on the cylinder, calculus on the sphere is different from calculus on the torus and so on. Suppose we have derivatives and integrals of all functions, on the former and on the latter, how can we tell the two apart? We state the idea above in the language of differential forms:
- “all vector fields with zero rotor are gradient” means
- “all closed $1$-forms are exact”.
This is true if and only if there are no tunnels. This happens on the plane and the sphere.
Discrete calculus makes things simpler. First, there are no limits. Second, the infinite-dimensional spaces of functions and forms are replaced with finite-dimensional ones. Third, the algebra of integers becomes a valid option...
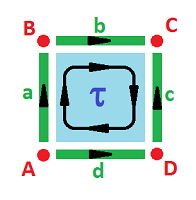
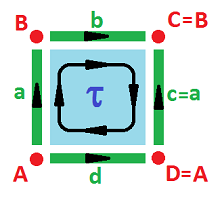
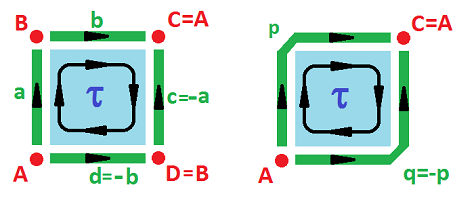
We first decompose the square into cells. The simplest choice is: four $0$-cells (vertices), four $1$-cells (edges), and one $2$-cell (a face):
We list below the cells' boundaries as chains (linear combinations) of cells: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-chains} & \partial & 1\text{-chains} & \partial & 0\text{-chains} \\ \hline & & \tau & \mapsto & \partial (\tau)=a+b-c-d \\ & & & & a & \mapsto & \partial (a)=B-A \\ & & & & b & \mapsto & \partial (b)=C-B \\ & & & & c & \mapsto & \partial (c)=C-D \\ & & & & d & \mapsto & \partial (d)=D-A \\ \end{array}$$ Invoking linear algebra now, we have Euclidean spaces with these generators and linear operators with these matrices: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} \text{}& & C_{2}=< \tau > & \ra{\partial} & C_{1}=< a,b,c,d > & \ra{\partial} & C_0 =< A,B,C,D > \\ &&& \left[\begin{array}{cc}1\\1\\-1\\-1\end{array}\right] && \left[\begin{array}{cc} -1&0&0&-1\\ 1&-1&0&0\\ 0&1&1&0\\ 0&0&-1&1 \end{array}\right]\\ \text{}& & C_{2}={\bf R} & \ra{\partial} & C_{1}={\bf R}^4 & \ra{\partial} & C_0 ={\bf R}^4 \end{array}$$ These spaces and operators form what is called the chain complex of the square.
Differential forms assign -- via integration -- a number to points, curves, surfaces, and solids, according to their degrees. Similarly, a discrete $k$-form simply assigns a number to each of the $k$-cells. They are dual of the chains and are called cochains. The main ones correspond to each cell and assign $1$ to the cell and $0$ to the rest. If the cell is $a$, this discrete form is denoted by $a^*$: $$a^*(a)=1\ \text{ and }\ a^*(b)=0.$$ The boundaries above give rise to the coboundaries, the replacements of the exterior derivatives, $$d=\partial^*,$$ of the cochains according to the following rule: $$\partial^*(a^*)(\tau)=a^*(\partial \tau).$$ These are the results: $$\begin{array}{ccrclclcccc} & & 2\text{-forms} &\partial^* & 1\text{-forms} &\partial^* & 0\text{-forms} \\ \hline & & \partial^*(a^*)=\tau^* & \leftarrowtail & a^* & & \\ & & \partial^*(b^*)=\tau^* & \leftarrowtail & b^* & & \\ & & \partial^*(c^*)=-\tau^* & \leftarrowtail & c^* & & \\ & & \partial^*(d^*)=-\tau^* & \leftarrowtail & d^* & & \\ & & & & \partial^*(A^*)=-d^*-a^* & \leftarrowtail & A^* \\ & & & & \partial^*(B^*)=a^*-b^* & \leftarrowtail & B^* \\ & & & & \partial^*(C^*)=b^*+c^* & \leftarrowtail & C^* \\ & & & & \partial^*(D^*)=-c^*+d^* & \leftarrowtail & D^* \\ \end{array}$$
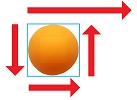
The meaning of a $1$-form is a flow along the edges and the meaning of its rotor, a $2$-form, is the amount of rotation of a ball placed in the flow:
Invoking linear algebra now, we have Euclidean spaces with these generators and linear operators $\partial^*$ with these matrices that happen to be the transposes of the ones of $\partial$: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} \text{}& & C^{2}=< \tau^* > & \la{\partial^*} & C^{1}=< a^*,b^*,c^*,d^* > & \la{\partial^*} & C^0 =< A^*,B^*,C^*,D^* > \\ &&&\left[\begin{array}{cc}1&1&-1&-1\end{array}\right]&&\left[\begin{array}{cc} -1&1&0&0\\ 0&-1&1&0\\ 0&0&1&-1\\ -1&0&0&1 \end{array}\right]\\ \text{}& & C^{2}={\bf R} & \la{\partial^*} & C^{1}={\bf R}^4 & \la{\partial^*} & C^0 ={\bf R}^4 \end{array}$$ It is called the cochain complex of the square. First, we confirm that the coboundary of the coboundary is zero: $$\begin{array}{ccccccccccc} \partial^*\partial^*=\left[\begin{array}{cc}1&1&-1&-1\end{array}\right]&\left[\begin{array}{cc} -1&1&0&0\\ 0&-1&1&0\\ 0&0&1&-1\\ -1&0&0&1 \end{array}\right]=0. \end{array}$$ It is the analog of the familiar: $\operatorname{rot}\operatorname{grad}=0$. Now, the kernel of the first linear operator (rank $1$), the exterior derivative of the $1$-forms, is $3$-dimensional. The image of the second linear operator (rank $3$), the exterior derivative of the $0$-forms, is $3$-dimensional, as well. In fact, these two are the same subspace of $C^1$! But the former is the closed $1$-forms and the latter is the exact $1$-forms. Therefore, we have, for the plane, again:
- “all closed $1$-forms are exact”.
For other cell decompositions, this conclusion will remain the same (according to Invariance of Cohomology).
Instead of decomposing the cylinder into cells, we create it from the square by an equivalence relation of its nine cells: $$a \sim c;\ A \sim D,\ B \sim C.$$
These are the cells and their boundaries: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-chains} & \text{boundary} & 1\text{-chains} & \text{boundary} & 0\text{-chains} \\ \hline \text{}& & \tau & \mapsto & b - d \\ & & & & a & \mapsto & B-A \\ & & & & b & \mapsto & 0 \\ & & & & d & \mapsto & 0 \\ \end{array}$$ This is the chain complex of the cylinder: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} \text{}& & C_{2}=< \tau > & \ra{\partial} & C_{1}=< a,b,d > & \ra{\partial} & C_0 =< A,B > \\ &&&\left[\begin{array}{cc}0\\1\\-1\end{array}\right]&&\left[\begin{array}{cc} -1&0&0\\ 1&0&0 \end{array}\right]\\ \text{}& & C_{2}={\bf R} & \ra{\partial} & C_{1}={\bf R}^3 & \ra{\partial} & C_0 ={\bf R}^2 \end{array}$$ These are the cochains: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-cochains} &\text{coboundary} & 1\text{-cochains} &\text{coboundary} & 0\text{-cochains} \\ \hline \text{generators:}& & 0 & \leftarrowtail & a^* & & \\ & & \tau^* & \leftarrowtail & b^* & & \\ & & -\tau^* & \leftarrowtail & d^* & & \\ & & & & -a^* & \leftarrowtail & A^* \\ & & & & a^* & \leftarrowtail & B^* \\ \end{array}$$ This is the cochain complex of the cylinder: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} \text{}& & C^{2}=< \tau^* > & \la{\partial^*} & C^{1}=< a^*,b^*,d^* > & \la{\partial^*} & C^0 =< A^*,B^* > \\ &&&\left[\begin{array}{cc}0&1&-1\end{array}\right]&&\left[\begin{array}{cc} -1&1\\ 0&0\\ 0&0 \end{array}\right]\\ \text{}& & C^{2}={\bf R} & \la{\partial^*} & C^{1}={\bf R}^3 & \la{\partial^*} & C^0 ={\bf R}^2 \end{array}$$ Now, the kernel of the first linear operator (rank $1$), the exterior derivative of the $1$-forms, is $2$-dimensional. The image of the second linear operator (rank $1$), the exterior derivative of the $0$-forms, is $1$-dimensional. These two can't be the same subspace of $C^1$! Therefore, we have for the cylinder, again:
- “not all closed $1$-forms are exact”.
In fact, it's easy to point out a non-exact closed $1$-form: $b^*+d^*$.
So, both calculus and discrete calculus detect, and are affected by, the tunnel of the cylinder.
Now, the second question, the orientability of the surfaces... While a tunnel is a $1$-dimensional topological feature, this one is $2$-dimensional. We will, therefore, concentrate on another part of the cochain complex.
Here's a simple computation on the plane: $$\operatorname{rot} <-y,0>=\operatorname{rot} <0,x> =1.$$ So, the constant function is the rotor of some vector field. We jump to the conclusion that all functions are. We can restate this idea in terms of differential forms, as follows:
- “all functions are rotors” means
- “all $2$-forms are exact”.
Does this hold for the projective plane? We make it from the square by gluing its edge to itself by identifying all pairs of antipodal points:
Is, this time, $1$ the rotor of some vector field? Even though neither $<-y,0>$ nor $<0,x>$ is properly defined on the projective plane, we can get another one: $$F= \left< -\frac{1}{2}y,\ \frac{1}{2}x \right>.$$ It is made from a rotation vector field $V=<-y,x>$ via division...
Its rotor is our constant function: $$\operatorname{rot}F=\operatorname{rot} \left< -\frac{1}{2}y,\ \frac{1}{2}x \right> =1.$$ We jump to the conclusion here that
- “all $2$-forms are exact”.
Now discrete calculus... The equivalence relation that makes the projective plane from the square is: $$p \sim q,$$ where $p=a+b$, $q=d+c$.
This is the chain complex of the projective plane with the generators identified: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-chains} & \text{boundary} & 1\text{-chains} & \text{boundary} & 0\text{-chains} \\ \hline \text{}& & \tau & \mapsto & 2p \\ & & & & p & \mapsto & 0 \\ \text{}& & C_{2} =< \tau > & \ra{\partial^*} & C_{1}=< p > & \ra{\partial^*} & C_0=< A > \\ &&&[2]&&[0]\\ \text{}& & C_{2} ={\bf R}^1 & \ra{\partial^*} & C_{1}={\bf R}^1 & \ra{\partial^*} & C_0={\bf R}^1 \\ \end{array}$$ From the boundaries we derive the coboundaries and from the chain complex we derive the cochain complex with the matrices of the coboundary operators: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-forms} &\partial^* & 1\text{-forms} &\partial^* & 0\text{-forms} \\ \hline \text{}& & 2\tau^* & \leftarrowtail& p^* & & \\ & & & & 0 & \leftarrowtail & A^* \\ \text{}& & C^{2}=<\tau^*> & \la{\partial^*} & C^{1} =< p^* > & \la{\partial^*} & C^0 =< A^* > \\ &&&[2]&&[0]\\ \text{}& & C^{2}={\bf R}^1 & \la{\partial^*} & C^{1}={\bf R}^1 & \la{\partial^*} & C^0 ={\bf R}^1 \end{array}$$ The former linear operator is the multiplication by $2$ and, therefore, is onto! So,
- “all $2$-forms are exact”.
This is the same as what we have for the plane. The topological difference is the non-orientability of the former but the forms behave the same way on both surfaces! Calculus will, therefore, fail to tell the projective plane from the plane.
So, we have shown that the real-valued calculus and discrete calculus fail to detect the non-orientability and tell the plane from the projective plane (or the cylinder from the Klein bottle, etc.).
Let's consider the integer-valued discrete calculus. First, because of the nature of the boundary operators and, therefore, coboundary operators, their matrices are integer-valued! Does the move from the reals to the integers make any difference then?
This is the cochain complex of the plane: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} \text{}& & C^{2}=< \tau^* > & \la{\partial^*} & C^{1}=< a^*,b^*,c^*,d^* > & \la{\partial^*} & C^0 =< A^*,B^*,C^*,D^* > \\ &&&\left[\begin{array}{cc}1&1&-1&-1\end{array}\right]&&\left[\begin{array}{cc} -1&1&0&0\\ 0&-1&1&0\\ 0&0&1&-1\\ -1&0&0&1 \end{array}\right]\\ \text{}& & C^{2}={\bf Z}^1 & \la{\partial^*} & C^{1}={\bf Z}^4 & \la{\partial^*} & C^0 ={\bf Z}^4 \end{array}$$ Nothing has changed except ${\bf R}$ is replaced with ${\bf Z}$. It still holds that
- “all $2$-forms are exact”, over ${\bf Z}$.
This is the cochain complex of the projective plane: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-forms} &\partial^* & 1\text{-forms} &\partial^* & 0\text{-forms} \\ \hline \text{}& & 2\tau^* & \leftarrowtail& p^* & & \\ & & & & 0 & \leftarrowtail & A^* \\ \text{}& & C^{2}=<\tau^*> & \la{\partial^*} & C^{1} =< p^* > & \la{\partial^*} & C^0 =< A^* > \\ &&&[2]&&[0]\\ \text{}& & C^{2}={\bf Z}^1 & \la{\partial^*} & C^{1}={\bf Z}^1 & \la{\partial^*} & C^0 ={\bf Z}^1 \end{array}$$ Nothing has changed except ${\bf R}$ is replaced with ${\bf Z}$. However, the former linear operator is the multiplication by $2$, which -- over the integers -- is not onto anymore! So,
- “not all $2$-forms are exact”, over ${\bf Z}$.
In fact, it is easy to point out a non-exact $2$-chain: $\tau^*$.
For other cell decompositions, the conclusion will continue to hold: some of the $2$-forms don't come from the rotors of flows.
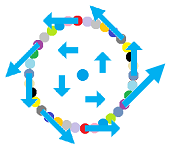
Specifically, the constant function on the $2$-cells with the smallest non-zero value, $1$, isn't one of them. Therefore, the balls on the projective plane can't rotate in unison at that speed. One will reach the same conclusion by simply following the rotations of the balls while making a full circle around the projective plane:
If we take a trip along an appropriate strip -- it's the Mobius strip -- of the projective plane, there will always be a conflict of directions at the end!
Thus, in contrast to the real-valued calculus, there is a difference between integer-valued calculus on the plane and integer-valued calculus on the projective plane. We have detected the non-orientability of the latter!
So, we needed the algebra of integers to detect non-orientability. Can we have “calculus over the integers”? Well, if the integral of a constant function over an interval is $1$, then what is the integral over a half of the interval? An infinite divisibility of the space implies an infinite divisibility of the ring of numbers...
Our conclusion is that calculus, as we know it, is unable to tell an orientable space from non-orientable!
Let's recast these results in the language of cohomology...
We use the cochain complex to find, over ${\bf R}$:
- the vector spaces of cocycles (the kernels of the coboundary operators) and
- the vector spaces of coboundaries (the images of the coboundary operators).
First, for the square and the plane, we have: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} & & 2\text{-cochains} & & 1\text{-cochains} & & 0\text{-cochains} \\ \hline \text{kernels (closed):} & & Z^2=<\tau^*> && Z^{1}=<a^*, b^*-d^* > & & Z^{0}=< A^*+B^* > \\ \text{images (exact):} & & B^2=<\tau^*> && B^{1}=< a^* > & & B^{0} = < 0 > \\ \text{quotients (cohomology):}& & H^2=0 && H^{1}=< [b^*]-[d^*] >\cong {\bf R}& & H^{0} = < [A^*]+[B^*] > \cong {\bf R} \end{array}$$ At the bottom, we compute the cohomology over ${\bf R}$ as the quotient of the cocycles over the coboundaries: $$H^k=Z^k/B^k.$$ So, the cohomology is identical to that of the circle but different from that of the plane (or a square). The conclusion doesn't change if we switch from the reals to the integers as the coefficient ring...
The de Rham cohomology $H^*_{dR}$ is defined the same way for the cochain complex of differential forms. It is known -- according to de Rham Theorem -- that the two cohomologies are isomorphic: $$H^*_{dR}(M;{\bf R})=H^*(M;{\bf R}),$$ for any smooth manifold $M$. So, the topological conclusions we derive from calculus, as we know it, are identical to those derived from discrete calculus over the reals.
We next use the cochain complex presented previously to find the cocycles and the coboundaries for the projective plane and then its cohomology: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} H^*({\bf RP}^2;{\bf R})& & 2\text{-cochains} & & 1\text{-cochains} & & 0\text{-cochains} \\ \hline \text{kernels (closed):} & & Z^2 = <\tau^*> && Z^1 = 0 & & Z^0 = < A^* > \\ \text{images (exact):} & & B^2 = <2\tau^*>=<\tau^*> && B^1 = 0 & & B^0 = 0 \\ \text{quotients (cohomology):}& & H^2=<\tau^*>/<\tau^*> \cong 0 && H^1 = 0 & & H^0 = < [A^*] > \cong {\bf R} \end{array}$$ Note how $B^2$ is simplified because we can divide. Same cohomology as the plane! Since $$H^2_{dR}({\bf RP}^2;{\bf R})=H^2({\bf RP}^2;{\bf R}),$$ we note, once again, that calculus, as we know it, is unable to tell an orientable space from non-orientable.
The chain complex and the cochain complex of the projective plane over ${\bf Z}$ consist of the modules of cocycles and coboundaries. Their generators are the same but the cohomology is different: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\la}[1]{\!\!\!\!\!\xleftarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{lccccccccccc} H^*({\bf RP}^2;{\bf Z})& & 2\text{-cochains} & & 1\text{-cochains} & & 0\text{-cochains} \\ \hline \text{kernels (closed):} & & Z^2 = <\tau^*> && Z^1 = 0 & & Z^0 = < A > \\ \text{images (exact):} & & B^2 = <2\tau^*> && B^1 = 0 & & B^0 = 0 \\ \text{quotients (cohomology):}& & H^2 = <\tau^*>/<2\tau^*>\cong {\bf Z}_2 && H^1 = 0 & & H^0 = < [A^*] > \cong {\bf Z} \end{array}$$ Note how $B^2$ is not simplified because we cannot divide. Different cohomology from the plane! The Universal Coefficient Theorem tells us that this is to be expected: the integer cohomology always gives us the real cohomology but not vice versa (as well as binary etc.).
The conclusions remain true for higher dimensions. For example, we have the following for a $3$-dimensional space. This is the $3$rd cohomology for the orientable Euclidean space vs. the non-orientable projective space: $$H^3_{dR}({\bf R}^3;{\bf R})=H^3_{dR}({\bf RP}^3;{\bf R})=0=H^3({\bf RP}^3;{\bf R})=H^3({\bf R}^3;{\bf R})=0.$$ Same, for the reals! But different for the integers: $$H^3({\bf R}^3;{\bf Z})=0 \ \ne\ H^3({\bf RP}^3;{\bf Z})={\bf Z}_2.$$ Once again, calculus, as we know it, cannot tell an orientable space from non-orientable, but the integer-valued one can.
There is a more interesting $3$-dimensional example. It is about electromagnetism.
If $E$ is the electric field and $B$ is the magnetic field (as functions of position and time), then the Maxwell–Faraday equation states: $$\operatorname{curl} E = − B',$$ where $B'$ is the time-derivative of $B$. In terms of differential forms, we have: $$de=-b',$$ where $e$ is a $1$-form and $b$ is a $2$-form (over space). So, for every choice of an electric field, there is a magnetic field. Conversely, in ${\bf R}^3$, every $2$-form is exact, therefore, there is an electric field for every magnetic field. In summary, they are paired up: there is an electromagnetic field. As we know, the reason for this is the fact that the de Rham $2$-cohomology of this space (and others such as the $3$-sphere) is trivial: $$H^2_{dR}({\bf R}^3;{\bf R})=0=H^2_{dR}({\bf S}^3;{\bf R})=0.$$ Otherwise, some choices of magnetic fields won't produce electric fields.
There are many spaces with a non-trivial $2$-cohomology, but let's take the product of the projective plane and the circle. From our previous computations for the projective plane and what we know about the circle, $$H^0({\bf S}^1;{\bf Z})={\bf Z},\quad H^1({\bf S}^1;{\bf Z})={\bf Z},$$ we derive, according to the Künneth Theorem: $$H^2({\bf RP}^2\times {\bf S}^1;{\bf R})=0 \ \ne\ H^2({\bf RP}^2\times {\bf S}^1;{\bf Z})={\bf Z}_2.$$ Once again, calculus, as we know it, cannot tell an orientable space from non-orientable, but the integer-valued one can.
Notes:
- The algebraic topology background is presented in my book Topology Illustrated.
- Discrete calculus (over any ring) is also presented in this book, including the part that requires a metric in order to handle lengths, areas, volumes, etc.
- On an elementary level, an exposition of discrete (real-valued) calculus is found in the draft of my other book Calculus Illustrated, along with calculus-as-we-know-it, starting with calculus of sequences (Chapter 1).
- In the preface to this book, I am making a case for teaching discrete calculus along or before calculus-as-we-know-it.
- Finally, how much do we really need to teach addition of fractions in elementary school?