This site is being phased out.
Calculus Illustrated -- preface
Calculus Illustrated by Peter Saveliev
History doesn't repeat itself but it often rhymes. -- Attributed to Mark Twain
Music is the pleasure the human mind experiences from counting without being aware that it is counting. -- Gottfried Leibniz
Contents
To the undergraduate student...
This book contains all math you need to know to be able to send a craft to the Moon.
The book is being written with undergraduates in mind, the ones, in fact, I have taught this material over the years.
Don't be intimidated by the length of the text. The core material would take much less room; most of the rest of the book is meant to explain and illustrate it. The material is often developed in manner of a slow ascend with reviews and even some repetitions. Some material is more advanced and is meant to be skipped if you face calculus for the first time. This applies (but not limited) to most of the proofs. Don't hesitate to move forward as fast as desired and then come back as necessary.
No need to memorize the formulas, initially. With enough time spent with the material, the main ones will eventually sink in. For the rest, you just need to be aware of them and be able to find the right one when necessary. Remember, formulas are easy, ideas are hard.
Spreadsheets (Microsoft Excel and its analogues) are used extensively for both illustrations and modeling. They are also to be used for projects. One can achieve as good results with packages specifically designed for physics simulations but I strongly encourage you to learn and use Excel. It is easy, it is universally applicable, it is installed on every PC, and it pays to know how to use it.
Some things are given in bold to separate them from the rest.
- Definition. New concepts are introduced -- to be used for reference -- with the term being defined given in italics. These concepts will re-appear a lot. They are to be remembered.
- Theorem. These are the most important facts and are to be remembered and to be used for reference. A theorem sometimes comes with its name included, in parentheses, as in Theorem (Fundamental Theorem of Calculus). Often, but not always, a theorem comes with a Proof. The proofs can sometimes be skipped at first reading. They end with $\blacksquare$.
- Notation. New notation and symbols are introduced -- to be used throughout the book.
- Example. Some of these can be skipped without violating of the flow of ideas, at your own risk. Examples end with $\square$.
- Exercise. These are the exercises to be done (or at least to consider) as you read the book.
Most of the in-text exercises are routine. They are not, however, repetitive (unless include “repeat”). Additional exercise sets are at the end of each part as well as online. Keep in mind that these exercises are no more than afterthoughts. They aren't what you study. In the hierarchy of importance, the short paragraphs that follow “Definition.” or “Theorem.” are at the very top.
Its highly detailed exposition makes the book a good choice for self-study.
To the graduate student...
This book contains all you need to know to be able to teach calculus.
I try to visualize everything, big or small. The pictures that come out are sometimes very precise but sometimes serve as mere metaphors for the concepts they illustrate. The hope is that they will serve as visual “anchors” in addition to the words and formulas.
There is little emphasis on closed-form computations and algebraic manipulations. I do think that a person who has never integrated by hand (or differentiated, or applied the quadratic formula, etc.) cannot possibly understand integration (or differentiation, or quadratic functions, etc.). However, a large proportion of time and effort can and should be directed elsewhere:
- understanding of the concepts and
- modelling in realistic settings.
The challenge of this approach is that it requires more rather than less abstraction.
The main formulas will have to be memorized, eventually.
Proofs are included for completeness; they are optional... unless, of course, you are to teach calculus at some point, then they aren't.
Most of the exercises are routine but they aren't what you study. If you understand the concepts, you’re doing fine. If you can follow the proofs, you’re great. And if you need a challenge, try to reproduce those proofs from memory. In a sense, every proof (and every example, etc.) is an exercise – with a solution!
Even if you are well-familiar with calculus, I suggest to start with the very first chapter called Calculus of sequences. It is dedicated entirely to discrete calculus. The chapter is meant to serve as a preview for those who are new at calculus and, for the rest, a review of the most fundamental ideas underlying calculus at their simplest.
To the teacher...
Most of the material comes from my lecture notes and the rest is something I have always wanted to talk about but never had the time. The book covers the standard material of Calculus 1-2-3 with a substantial review of precalculus and a preview of elementary ordinary and partial differential equations.
In the order of topics, the main difference from a typical textbook is: sequences before everything else. The reasons are:
- sequences are simpler than functions;
- limits of sequences are simpler than limits of functions (including the ones at infinity);
- the sigma-notation, the Riemann sums, and the Riemann integral without a sequences background is a challenge;
- a single section devoted to sequences followed by a quick transition to series often leads to confusion between the two;
- sequences are needed for modeling, which should start as early as possible.
It is unlikely that a person who has never plotted the graph of a function by hand can understand graphs or functions. However, what if we want to plot more than just a few points in order to visualize curves, surfaces, vector fields, etc.? Spreadsheets were chosen over graphic calculators for visualization purposes because they represent the shortest step from pen and paper: one cell - one number - one point on the graph. For more advanced tasks such as modelling, spreadsheets were chosen over other software and programming options for their wide availability and, above all, their simplicity. Nine out of ten, the spreadsheet shown was created from scratch in front of the students who were later able to follow the steps and create one of their own.
If at all possible, please don't make the student memorize the formulas, at least not until the end of the semester.
From the discrete to the continuous
It's no secret that a vast majority of calculus students will never use what they have learned. Poor career choices aside, a former calculus student might have trouble recognizing mathematics that surrounds him. Why is this happening?
Calculus is the science of change. From the very beginning, its peculiar challenge has been to study and measure continuous change: curves and motion along curves. These curves and this motion are given by formulas. Skillful manipulation of those formulas is what solves calculus problems. This approach was taken over 300 years ago and it has been extremely successful in sciences and engineering. The successes are well-known: projectile motion, planetary motion, flow of liquids, heat transfer, wave propagation, etc. The common way of teaching calculus follows this approach; an overwhelming majority of what the student does is manipulation of formulas on a piece of paper. As a result, all the problems the student faces were (or could have been) solved in the 18-19th century.
What has changed since? The computers have appeared, of course, and computers don't manipulate formulas. They can't solve -- in the traditional sense of the word -- those problems from the past centuries. Instead of continuous, computers excel at handling incremental processes and instead of formulas they are great at managing discrete (digital) data. That is why we apply various numerical methods to the results produced by calculus in order to generate algorithms that manipulate such data. The solutions are approximate but the applicability is unlimited. This approach was taken in the 20th century and it has been extremely successful in sciences and engineering. It is also circuitous: every concept in calculus starts -- often implicitly -- as a discrete approximation of a continuous phenomenon!
Calculus is the science of change, both incremental and continuous. The former part -- the so-called discrete calculus -- may be seen as the study of incremental phenomena and quantities indivisible by their very nature: people, animals, and other organisms, moments of time, locations of space, particles, some commodities, digital images and other man-made data, etc. With the help of the calculus machinery, called “limits”, we transition to the continuous part of calculus, especially when we face continuous phenomena and quantities infinitely divisible either by nature or by assumption: time, space, mass, temperature, money, some commodities, etc. Calculus produces definitive results and absolute accuracy but only for problems amenable to its methods. In the classroom, problems are simplified until they become manageable or, otherwise, we have to circle back to the discrete methods in search of approximations.
Within a typical calculus course, the student simply never gets to complete the “circle”! Later on, the graduate is likely to think of calculus only when he sees formulas and unlikely when he sees numerical data.
In this book, every concept of calculus is introduced in its discrete, “pre-limit”, incarnation -- otherwise commonly hidden inside proofs -- first and then used for modelling and applications well before its continuous counterpart emerges. The properties of the former are discovered first and then the matching properties of the latter are found by making the increment smaller and smaller, at the limit: $$\newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \begin{array}{ccccc} \begin{array}{|cc|}\hline\text{ discrete }\\ \text{ calculus }\\ \hline\end{array}& \ra{\quad\Delta x\to 0\quad} &\begin{array}{|cc|}\hline\text{ continuous }\\ \text{ calculus }\\ \hline\end{array} \end{array}$$
Even though there are no plans to translate the book, here is a translation into Russian of this part.
От дискретного к непрерывному
Не секрет, что подавляющее большинство студентов, изучающих курс математического анализа, никогда не будут использовать то, чему они научились. Потому что, помимо проблем с выбором карьеры, бывший студент часто не распознает математики, которая, как мы знаем, его окружает. Почему это происходит? Дифференциальное исчисление - это наука об изменениях. С самого начала его задачей было изучение и измерение непрерывных изменений: кривых и движения вдоль кривых. Эти кривые и это движение представлены формулами. Умелое манипулирование этими формулами - вот что решает проблемы дифференциального исчисления. Более 300 лет этот подход был чрезвычайно успешным в науке и технике. Успехи общеизвестны: движение снаряда, движение планет, движение потока жидкости, теплопередача, распространение волн и т. д. Соответствующий метод обучения основан на том же самом подходе: подавляющее большинство того, что делает студент, - это манипулирование формулами на листе бумаги. Но это означает, что все проблемы, с которыми сталкивается студент, были (или могли быть) решены в XVIII или XIX веках!
Этого недостаточно. Что изменилось с тех пор? Конечно, появились компьютеры, которые не манипулируют формулами. Они не помогают в решении - в традиционном смысле этого слова - проблем прошлых веков. Вместо этого компьютеры превосходно решают инкрементные задачи, а вместо формул они отлично справляются с дискретными (цифровыми) данными. Чтобы использовать эти преимущества, ученые «дискретизируют» результаты дифференциального исчисления и создают алгоритмы, которые манипулируют цифровыми данными. В результате, решения являются приблизительными, но их применимость не ограничена. С ХХ века этот подход был чрезвычайно успешным в науке и технике: аэродинамика (проектирование самолетов и автомобилей), обработка звука и изображений, исследование космоса, структуры атома и вселенной и т. д. Этот подход круговой - ведь каждая концепция в дифференциальном исчислении начинается - часто неявно - как дискретное приближение непрерывного явления!
Дифференциальное исчисление - это наука об изменениях, как инкрементных (постепенных), так и непрерывных. Первая часть - так называемое дискретное исчисление - может рассматриваться как исследование инкрементных явлений и величин, неделимых по своей природе: люди, животные и другие организмы, моменты времени, места в расположение в пространстве, элементарные частицы, некоторые товары, цифровые изображения и другие искусственные данные и т. д. С помощью конструкции, называемой «предел», мы неизменно переходим к непрерывной части дифференциального исчисления, особенно когда мы сталкиваемся с бесконечно делимыми, непрерывными явлениями и величинами, либо по их природе или предположению: время, пространство, масса, температура, деньги, некоторые товары и т. д. Дифференциальное исчисление дает окончательные результаты и абсолютную точность, но только для задач, поддающихся его методам! В системе образования проблемы упрощаются до тех пор, пока они не становятся приемлемыми; в противном случае мы возвращаемся к дискретным методам в поисках приближений.
В рамках типичного курса по дифференциальному и интегральному исчислению студент просто не может завершить этот «круг»! Позже, выпускник, вероятно, вспомнит об этом курсе, только когда увидит формулы, и редко, когда он увидит числовые данные. В этой книге каждая концепция дифференциального и интегрального исчисления сначала вводится в ее дискретном, «предлимитном» воплощении - обычно скрытом внутри доказательств - и затем используется для моделирования и приложения задолго до появления ее непрерывного аналога. Сначала исследуются свойства первого, а затем соответствующие свойства второго выводятся путем предельного перехода.
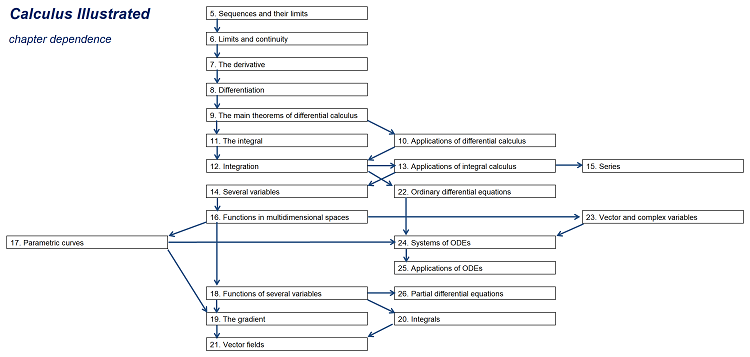
The chapter dependence chart
Below, $A\to B$ means that chapter $B$ shouldn't be read before chapter $A$. The material in the precalculus chapters, 1-4, are assumed to be known.