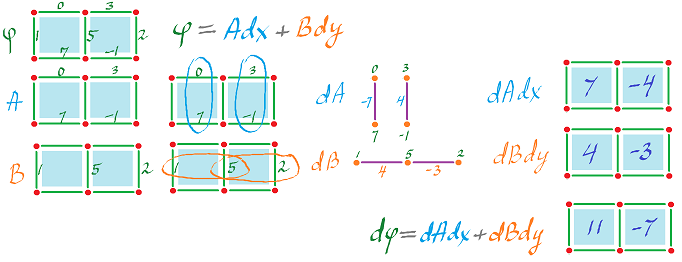This site is being phased out.
Algebraic operations with forms and cohomology
What about integration over "longer" intervals, not just cells?
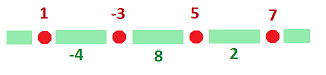
Easy: for $a,k \in {\bf Z}$, $$\displaystyle\int_{[a,a+k]} = \displaystyle\int_{[a,a+1]} df + \displaystyle\int_{[a+1,a+2]}df + \ldots + \displaystyle\int_{[a+k-1,a+k]} df $$ $$= f(a+1)-f(a) + f(a+2) - f(a+1) + \ldots + f(a+k) - f(a+(k-1)) $$ $$= f(a+k) -f(a).$$
So, we can now integrate over chains.
Works under: $\displaystyle\int_{[a,a+1]}df = f(a+1) - f(a).$
We will assume the following: $R$ is any cubical complex, i.e., a set of cells such that if cell $s \in R$, then all of its boundary cells also belong to $R$.
Dimension $1$: (degree $1$) Given $0$-form $f$:
Formula still works: $$df = f' dx,$$ where $f'[a,a+1] = f(a+1)-f(a)$, the difference.
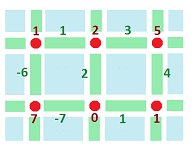
Dimension $2$: (degree $1$) See $0$-form $f$. Exterior derivative $df$:
Continuous and discrete: $$df = \nabla f \cdot dA,$$ where $dA = (dx,dy)$ and $\nabla f = (f_x,f_y)$.
Compute:
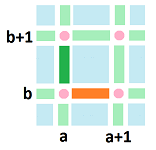
- 1.) $f_x([a,a+1] \times \{b\}) = f(a+1,b) - f(a,b)$
- 2.) $f_y(\{a \} \times [b,b+1]) = f(a, b+1) - f(a,b)$. So, $df = f_x' dx + f_y' dy$.
What about higher order exterior derivatives?
We have used this "definition":
If $\varphi \in C^k$ then $d \varphi \in C^{k+1}$ and $d \varphi$ is obtained from $\varphi$ by applying $d$ to each of the functions involved in $\varphi$.
Let's apply it to discrete forms.
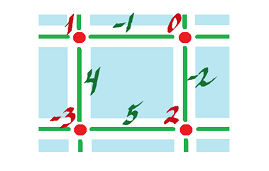
Example: $\varphi = A dx + B dy$, then $d \varphi = dA \hspace{1pt} dx + dB \hspace{1pt} dy$. What about co-chain?
Subtract vertically and horizontally:
Then, $dA = (0-7)dy = -7 dy$ which is
on $\alpha$.
$dA = (3 - (-1))dy = 4 dy$ on $\beta$.
Further:
$dB = (5-1)dx = 4dx$ on $\alpha$.
$dB = (2-5)dx = -3dx$ on $\beta$.
So, evaluated on $\alpha$, using antisymmetry to get the third line,
$\begin{align*} d \varphi &= dA \hspace{1pt} dx + dB \hspace{1pt} dy\\ &= -7 dy \hspace{1pt} dx + 4 dx \hspace{1pt} dy \\ &= 7 dx \hspace{1pt} dy + 4 dx \hspace{1pt} dy \\ &= 11 dx \hspace{1pt} dy. \end{align*}$
On $\beta$: $d \varphi = (4+3) dx \hspace{1pt} dy$.
$(5-1) - (0-7)$
$(2-5) - (3-(-1)) = -7$
How: horizontal difference $-$ vertical difference.
This is similar to smooth forms. Recall: $d(A dx + B dy) = (B_x - A_y)dx \hspace{1pt} dy$ (above)
Theorem: $d \colon C^k(R) \rightarrow C^{k+1}(R)$ is linear.
Theorem: (Product Rule/Leibniz Rule) $d(\varphi \psi) = d \varphi \cdot \psi + (-1)^k \varphi d \psi$.
Theorem: $dd \colon C^k(R) \rightarrow C^{k+2}(R)$ is zero.
For $R = {\bf R}^2$, $k=0$, proof is easy.
- $0$-form $f$ given:
- Compute $1$-form $df$.
- Compute $2$-form.
$\begin{align*} d(df) &= (B_x - A_y) dx \hspace{1pt} dy \\ &= ((-2 -4) - (-1 -5))dx \hspace{1pt} dy \\ &= 0. \end{align*}$
HOMEWORK: Prove $dd \colon C^1({\bf R}^3) \rightarrow C^3({\bf R}^3)$ is zero.
Smooth forms: $\Omega^1({\bf R})$, $1$-forms in ${\bf R}$ and $\Omega^0({\bf R})$, and $0$-forms in ${\bf R}$ are both vector spaces.
Also ${\rm dim} \Omega^0({\bf R}) = {\rm dim} C({\bf R}) = \infty$!
$\{1, x, x^2, \ldots\}$ is linearly independent (${\rm span} \leftarrow$ Taylor series).
${\rm \dim} {\bf R} =1$ (constant function)
Proof: Not all $a_0, \ldots, a_n$ are $0$:
$a_0+a_1x+a_2x^2+\ldots+a_nx^n = 0$?
This series is a function for every $x$.
In particular, $x=0$, so $a_0=0$ implying $a_1x+a_2x^2+\ldots+a_nx^n = 0$ \ldots = $x(a_1+a_2x+\ldots+a_nx^{n-1}) = 0$. But $x \neq 0$ for all $x$, so $a_1 + a_2x + \ldots+a_n x^{n-1}=0$.
Observe ${\rm dim} C^0[0,k] = k+1 < \infty$! Everything is computable!
From HOMEWORK: $[a,b] + [b,c] \sim [a,c]$ (definition).
- 1.) $[a,b] \sim [a,b]$
- 2.) $[a,b] \sim [c,d]$ implies $[c,d] \sim [a,b]$ (Symmetry)
- 3.) etc
To verify, rewrite $[a,b]+[b,c] \sim [a,d]+[d,c]$.
Also this: $[a,a] + [a,c] = 0 + [a,c]$, since $[a,a]$ is a $0$-cell and $[a,c]$ is a $1$-cell.
Generally, if $R$ is a cubical complex, ${\rm dim} C^k(R) = $ number of $k$-cells in $R$.
$\varphi \colon {\rm cell} \rightarrow {\rm a \hspace{3pt} number}$
$\ldots \stackrel{d_{k-1}}{\rightarrow} C^k \stackrel{d_k}{\rightarrow} C^{k+1} \stackrel{d_{k+1}}{\rightarrow} C^{k+2} \stackrel{d_{k+2}}{\rightarrow} \ldots$
These are vector spaces: ${\rm ker \hspace{3pt}} d_k$ is the set of closed $k$-forms, also known as cocycles and ${\rm im \hspace{3pt}} d_{k-1}$ is the set of exact $1$-forms, also known as coboundaries.
Since $dd=0$, then "every exact form is closed" or every coboundary is a cocycle (Poincare Lemma):
$${\rm im} d_{k-1} \subset {\rm ker \hspace{3pt}} d_k$$
Define the cubical cohomology (of $R$) as $H^k(R)={\rm ker \hspace{3pt}} d_k / {\rm im \hspace{3pt}} d_{k-1}$.
Proposition: Constant functions are closed forms (defined on vertices!).
Proof: If $\varphi \in C^0({\bf R})$, $d \varphi([a,a+1]) = [\varphi[(a+1)-\varphi(a)]dx = 0dx = 0$. (same for $C^0({\bf R}^n)$).
Proposition: Closed $0$-forms are constant on a path-connected cubical complex.
Proof: ${\bf R}^1$: $d \varphi([a,a+1]) = 0$, so $(\varphi(a+1) - \varphi(a))dx = 0$, so $\varphi(a+1) = \varphi(a)$, so $\varphi$ is constant on adjacent vertices.
Lemma: path-connected $\longleftrightarrow$ any two vertices can be connected by edges. (Easy)
Use it to finish the proof. (same for ${\rm dim \hspace{3pt}} 2$
Corollary: ${\rm dim \hspace{3pt} ker \hspace{3pt}} d_0 =$ number of path components.
What about the exact $0$-forms?
Just one, $0$.
To summarize:
Theorem: $H^0(R) = {\bf R}^m$, where $m$ is the number of path components of $R$.
Recall this fact about smooth forms: if $R$ is simply connected, then all closed forms are exact.
Hence $\Omega_{dR}^1(R) = 0$. Same for discrete: $H^1(R)=0$.
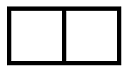
Example: Let's detect the hole in the circle. Let $R = $ 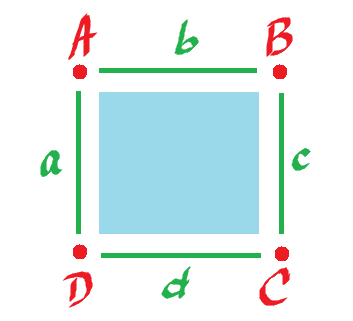 .
.
Compute $H^1(R)$. Consider the sequence $C^0 \stackrel{d_0}{\rightarrow} C^1 \stackrel{d_1=0}{\rightarrow} C^2 = 0$ (note: ${\rm ker \hspace{3pt}} d_1 = C^1$)
List the bases:
| $\varphi_1$ | $\varphi_2$ | $\varphi_3$ | $\varphi_4$ | |
| A | 1 | 0 | 0 | 0 |
| B | 0 | 1 | 0 | 0 |
| C | 0 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 1 |
| $\psi_1$ | $\psi_2$ | $\psi_3$ | $\psi_4$ | |
| a | 1 | 0 | 0 | 0 |
| b | 0 | 1 | 0 | 0 |
| c | 0 | 0 | 1 | 0 |
| d | 0 | 0 | 0 | 1 |
Find the formula for $d_0$, a linear operator, so we need its matrix, $4 \times 4$.
Just look at what happens to the basis elements:
$\varphi_1 =$ 
|
$d_0 \varphi_1 =$ 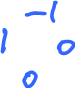 $= \psi_1-\psi_2$ $= \psi_1-\psi_2$
|
$\varphi_1 =$ 
|
$d_0 \varphi_1 =$  $= \psi_1-\psi_2$ $= \psi_1-\psi_2$
|
$\varphi_1 =$ 
|
$d_0 \varphi_1 =$  $= \psi_1-\psi_2$ $= \psi_1-\psi_2$
|
$\varphi_1 =$ 
|
$d_0 \varphi_1 =$  $= \psi_1-\psi_2$ $= \psi_1-\psi_2$
|
Find ${\rm im \hspace{3pt}} d_0$.
It's $C^1$.
Why? Check, are the columns linearly independent? No (just take the sum). Then $${\rm span}\{ d_0(\varphi_1),d_0(\varphi_2),d_0(\varphi_3),d_0(\varphi_4)\} \neq C^1.$$
Better way: ${\rm det \hspace{3pt}} d_0 = 0$, $d_0$ is not onto.
The image is a proper subspace. What's its dimension?
$d_0(\varphi_1) + d_0(\varphi_2) + d_0(\varphi_3) + d_0(\varphi_4) = 0$, so we can take one out: ${\rm span} \{ d_0(\varphi_1), d_0(\varphi_2), d_0(\varphi_3) \} = {\rm im \hspace{3pt}} d$. More? No, these are linearly independent (verify).
In fact, ${\rm rank \hspace{3pt}} d_0 = 3$ (${\rm det \hspace{3pt}} d_0 = 0$, so ${\rm dim \hspace{3pt} im \hspace{3pt}} d_0 < 4)$)
So, $H^1(R) = {\rm ker \hspace{3pt}}d_0 / {\rm im \hspace{3pt}} d_0 = {\bf R}^4 / {\bf R}^3 \simeq {\bf R}$.