This site is being phased out.
Robustness of topology
Redirect to:
The analysis of the robustness of the topology of digital images may start with this simple principle:
Then adding a single pixel shouldn't dramatically change the topology of the image. But it does! The example on the right shows that adding the red pixel merges three objects and also creates a hole (white object).
The we can say that these topological features aren't robust. In fact the robustness can be measured in term of how many dilations and erosions it takes to change the topology. These are the types of questions we need to answer:
- how many erosions does it take to split an object into two or more or make it disappear?
- how many dilations does it take to create a hole in an object or merge two objects?
- etc.
For example, an object separated from others will have higher robustness under dilation that one with closed neighbors. A round object will have higher robustness under erosion than an elongated one.
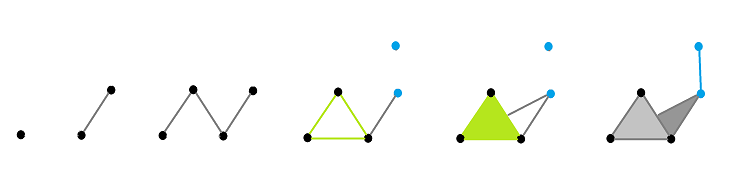
Parametrized complexes come from thresholding gray scale images and the Vietoris-Rips construction:
What we need is a way to measure robustness of the topological features of images. Besides robustness under dilation and erosion we will also take care of robustness under other transformations: translations, rotations, noise, blur etc.
The features we are concerned about are the homology groups: $$ K^{1}\hookrightarrow K^{2}\hookrightarrow K^{3}\hookrightarrow K^{4}% \hookrightarrow\ldots\ \hookrightarrow K^{s},$$ where the arrows represent the inclusions: $$i^{n,n+1}:K^{n}\hookrightarrow K^{n+1}.$$
and their homology: $$H_{\ast}(K^{1})\rightarrow H_{\ast}(K^{2})\rightarrow\ldots\ \rightarrow H_{\ast}(K^{s})\longrightarrow0. $$ These homomorphisms are induced by the inclusions and they record how the homology changes as the complex grows at each step. For example, a component appears, grows, and then merges with another one, or a hole is formed, shrinks, and then is filled. We refer to these events as birth and death of the corresponding homology class.
In order to evaluate the robustness of an element of one of these groups the persistence of a homology class is defined as the number of steps in the homology sequence it takes for the class to end at $0$:
- persistence = death date - birth date.
The $p$-persistent homology group of $K^{i}$ is defined as the image of $i_{\ast}^{i,i+p}.$ It is what's left from $H_{\ast}(K^{i})$ after $p$ steps in the filtration. Now the robustness of the homology classes of the filtration is evaluated in terms of the set of intervals $[birth,death]$ representing the life-spans, called barcodes, of the homology classes.
Our approach is similar but more algebraic. It consists of two steps.
First stage: we pool all possible homology classes in all elements of the filtration together in a single algebraic structure. The presence of noise at this point is ignored. The homology group $H_{\ast }(\{K^{n}\})$ of filtration $\{K^{n}\}$ captures all homology classes in the whole filtration -- without double counting. The latter is achieved by an equivalence relation that equates the classes that, in a sense, represent the same homology class in the filtration: $y=i_{\ast}^{n,n+1}(x)$.
Second stage: for a given positive integer $p,$ the $p$-noise group $N_{\ast}^{p}(\{K^{n}\})$ is comprised of the homology classes in $H_{\ast}(\{K^{n}\})$ with the persistence less than $p.$
Next, we "remove" the noise from the homology group of filtration by using the quotient: $$H_{\ast}^{p}(\{K^{n}\})=H_{\ast}(\{K^{n}\})/N_{\ast}^{p}(\{K^{n}\}). $$ In other words: if the difference between two homology classes is deemed noise, they are equivalent. This is the persistent homology group of filtration. The second stage can be repeated as needed.
The (persistent) homology group of filtration is a graded group and is intended to stand for the homology group of the data set that is behind the filtration.
In the case of image analysis, the homology group of the image, unlike the barcodes, captures only the topology independent from the gray levels. This is why one might say that our approach provides a coarser classification of the homology of filtrations.
Exercise: Consider another approach to robustness of -- via Hausdorff distance.