Quotients of complexes

Redirect to:

• Cell complex

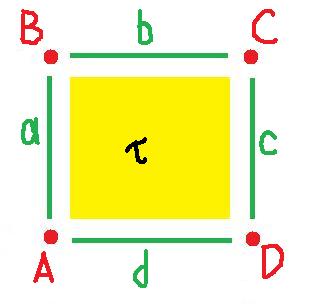
Let's consider how we build the cylinder from the square. The complex $K$ of the square is: $$\begin{array}{l} 0{\rm -cells}: A, B, C, D \\ 1{\rm -cells}: a, b, c, d \\ 2{\rm -cells}: \tau \end{array}$$

$${\rm Boundary \hspace{3pt} operator:} \partial \tau = a + b + c + d; \partial a = A + B, \partial b = B + C, {\rm \hspace{3pt} etc.}$$

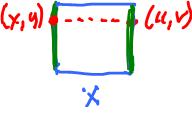
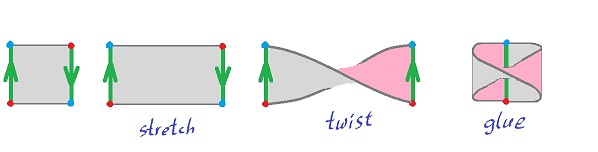
Now, we can create the cylinder $C$ by gluing two opposite edges with the following equivalence relation: $$(0,y) \sim (1,y).$$

But what about complexes? Can we interpret the gluing as equivalence of $a$ and $c$? Yes, but we also have to take care of the other cells as well: $$a \sim c,$$ $$A \sim D, B \sim C.$$

Certainly, this is not a cubical complex! But the we sill have our collection of cells (same exactly) only the boundary operator is different: $$\partial \tau = a + b + c + d = a + b + a + d = b + d,$$ $$\partial a = A + B, \partial b = B + C = 0, \partial c = A + B, \partial d = D + A = 0$$

Now, the chain complex of $K$ can be defined and its homology computed. The second line indicates that $b$ and $d$ are cycles and the first indicates that they are homologous. Hence $$H_1(C)= {\bf Z}_2.$$

Suppose now that we want to build the Mobius band ${\bf M}$. The equivalence relation is is given by $$(0,y) \sim (1,1-y).$$

Once again we can interpret the gluing as equivalence of $a$ and $c$. But this time they are attached to each other with $c$ upside down. It makes sense then to interpret this as an equivalence: $$a \sim -c,$$ $$A \sim D, B \sim C.$$

The boundary operator is: $$\partial \tau = a + b + c + d = a + b - a + d = b + d,$$ $$\partial a = A + B, \partial b = B + C = 0, \partial c = A + B, \partial d = D + A = 0$$

Same! Hence $$H_1({\bf M})= {\bf Z}_2.$$

Exercise. What do you get if you identify the boundary of the Mobius band to a single point? Solution:

A special kind of a quotient complex is seen when a subcomplex is collapsed to a single point. Given complex $X$ and a subcomplex $A$, the equivalence relation is defined by:

• $x \sim y$ for all $x,y \in A.$

Then we use the notation: $$X/A$$ (read "$X$ mod $A$").

In particular:

• ${\bf S}^1 = [0,1]/ \{0,1 \},$
• ${\bf S}^1 = {\bf R}/(- \infty,0] \cup [1, \infty).$

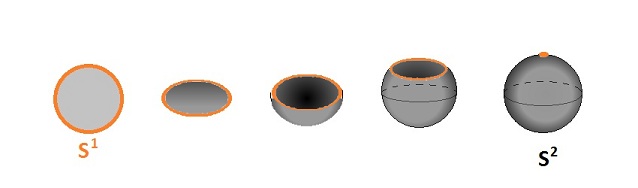
Also, one can construct the sphere ${\bf S}^2$ from the disk ${\bf D}^2$ by collapsing its boundary to a point:

• ${\bf S}^2 = {\bf D}^2/{\bf S}^1.$

Exercise. Try to glue together the opposite faces of a cube, one pair at a time...