Modelling motion on manifolds

Redirect to:

• ODEs

Let's recall how we describe motion in the Euclidean space. It is given by an ordinary differential equation (ODE): $$x'(t)=f(x(t)),$$ where $f:{\bf R}^n \to {\bf R}^n$ is a continuous vector field and $x:I \to {\bf R}^n$ is a differentiable parametric curve defined on an open interval $I$.

What about motion on manifolds?

We want to model a fluid flow. Then $x$ is the position of a given particle on manifold $M$ as a function of time $t$ and $f(x)$ is the velocity of this particle (or any other) if it happens to be at point $x$.

Recall that if we take all parametric curves through $a$ in $M$, then the union of all the tangent vectors at $a$ they produce is a vector space, $T_aM$, called the tangent space.

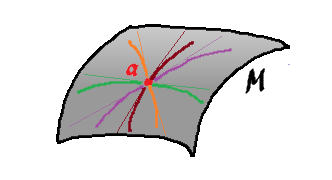
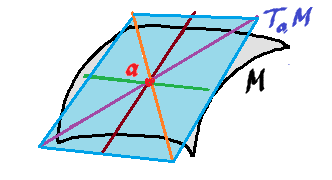
So, the velocity vector $f(x)$ belongs to the tangent space $T_xM$ of $M$ at $x$: $$f(x) \in T_xM.$$ But how do we capture this behavior for the whole $f$?

Recall that the tangent bundle of a manifold $M$ is $$TM = \displaystyle\bigsqcup_{a \in M} T_aM,$$ the disjoint union of all tangent spaces.

It follows first that $f$ is a function from $M$ to the tangent bundle of $M$: $$f:M \to TM.$$ In addition, $f$ has to respect the projection $p_M$ of the bundle: $$p_Mf=Id_M.$$ Under these conditions $f$ is called a vector field on manifold $M$.

With that in mind, the equation looks the same: $$x'(t)=f(x(t)).$$

We recast this problem in terms of differential forms as $$dx=f(x)dt.$$ All the parts are familiar, $u$ is still a parametric curve $$x:[0,1] \to M,$$ and a vector-valued $0$-form.

However, what about $dx$? In this setting we can't treat it coordinate-wise as in the Euclidean case,

• $x=(x_1,x_2,...,x_n)$, where each $x_i$ is a real-valued form, and
• $dx=(dx_1,dx_2,...,dx_n).$

Even though we can't use those, it is clear that vector-valued $1$-forms, velocities, should have their values in the tangent bundle of $M$!