Examples of maps

Redirect to:

• Continuous functions

There are several large classes of functions that are always continuous. The proof of that below relies on the relevant point-set topology. However, it's unnecessary if only subsets of the Euclidean space are involved. In that case we can use what we know about continuity of functions of several variables (see also Topology via Calculus).

Constant maps

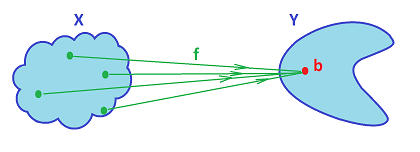
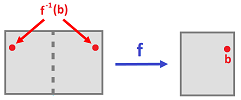
Suppose we have topological spaces $X$ and $Y$, the for any given $b \in Y$ we can define a constant function $f: X {\rightarrow} Y$ by

$f(x) = b$ for all $x \in X$.

This function is continuous, no matter what topologies $X$ and $Y$ have.

Indeed, suppose $U$ is open in $Y$. Then we have two cases:

• Case 1: $b \in U \Rightarrow f^{-1}(U) = X$, which is open.
• Case 2: $b \in X \setminus U \Rightarrow f^{-1}(U) = \emptyset$, which is open too.

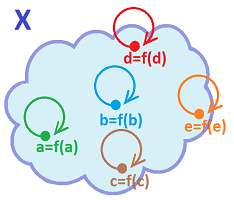
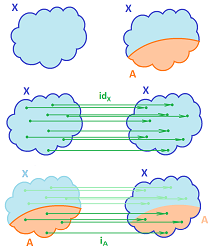
The identity map

Suppose we have a topological space $X$, then we we can define the identity function $i_X: X {\rightarrow} X$ by

$f(x) = x$ for all $x \in X$.

It is of course continuous, because $$f^{-1}(U) = U.$$

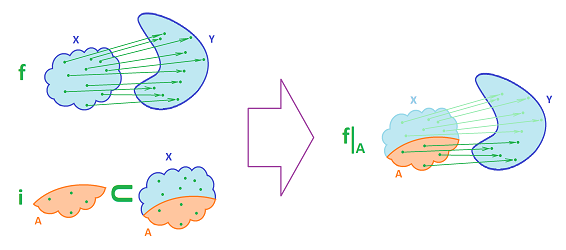
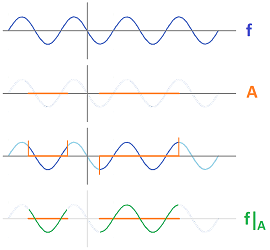
Restrictions

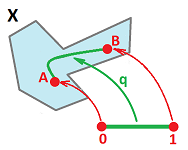
Suppose we have topological spaces $X$ and $Y$, a map $f: X \rightarrow Y$, and a subset $A$ of $X$. Then the restriction $f|_A: A {\rightarrow} Y$ of $f$ to $A$ is defined by

$f|_A(x) = f(x)$ for all $x \in A$.

It is always continuous, which follows directly from the definition of relative topology.

Theorem. The restriction of a continuous function is continuous.

Proof. Suppose we have a continuous function $f \colon X \rightarrow Y$ and a subset $A$ of $X$. Then the restriction $f_A \colon A \rightarrow Y$ of $f$ satisfies $f_A(x) = f(x)$ for all $x \in A$. Suppose $U$ is open in $Y$. Then $$f_A^{-1}(U) = f^{-1}(U) \cap A.$$ As the intersection an open, in $X$, set with $A$, this set is open in $A$. Hence $f_A$ is continuous. $\blacksquare$

Extensions

Inclusions

Suppose we have a topological space $X$ and a subset $A$ of $X$. Then the inclusion function $i_A: A {\rightarrow} X$ of $f$ is given by

$i_A(x) = x$ for all $x \in A$.

We can understand inclusions as restrictions of the identity maps.

From the definition of relative topology:

Theorem. The inclusion of a subset is continuous.

One can think of the projection $p: {\bf R}^2 {\rightarrow} {\bf R}$ as a self-map $p': {\bf R}^2 {\rightarrow} {\bf R}^2$ given by $p' = i_Rp$, where $i_R: {\bf R} {\rightarrow} {\bf R}^2$ is the inclusion of the $x$-axis into the plane.

Projections

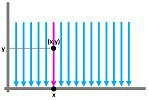
Let's start with the simple projection of the $xy$-plane on the $x$-axis, $p: {\bf R}^2 {\rightarrow} {\bf R}$. It is given by $$p(x,y) = x.$$

For each $b, p(x,b) = x$ is continuous function as it's the identity. For each $a, p(a,y) = a$ is continuous as a constant function. Therefore $p$ is continuous (cf. Continuity of functions of several variables).

What about the projection of the square $[0,1] \times [0,1]$ to the $x$-axis? It is continuous as the restriction of the map $p$ above. Then any subset in the plane can be projected to the $x$-axis.

More generally, if we have the product of topological spaces we can define a projection in the same manner: $$p_X: X \times Y {\rightarrow} X, p(x,y) = x.$$

In fact, the product creates two projections: $$p_X \colon X \times Y \rightarrow X {\rm \hspace{3pt} and \hspace{3pt}} p_Y \colon X \times Y \rightarrow Y {\rm \hspace{3pt} given \hspace{3pt} by}$$ $$p_X(x,y) = x, p_Y(x,y) = y.$$

Theorem. The projections are continuous.

Proof. Suppose $V$ is open in $X$. Then $f^{-1}(V) = V \times Y$ which is open in $X \times Y$ in the product topology since $Y$ is open in $Y$. $\blacksquare$

The projection of the cylinder on the circle is intuitively continuous - you can imagine how it collapses down on the plane:

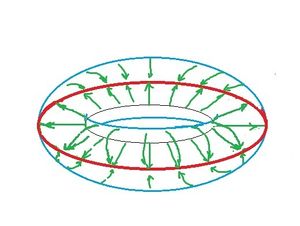
Projection of torus $p \colon {\bf T}^2 \rightarrow {\bf S}^1$ isn't as obvious as it might seem that in order to map it onto one of the longitude you'd have to tear it:

A more general concept is that of a self-projection which is any self-map $P:X \to X$ that satisfies $PP=P$.

Exercise. Think of a non-constant self-projection of the Mobius band.

Identifications

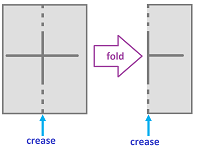
Consider first folding of the $xy$-plane, $$f(x,y) = (|x|,y).$$

It is Continuity of functions of several variables.

Now, the folding of the rectangle $[-1,1] \times [0,1]$ is given by the same formula and is continuous as a restriction of $f$.

Gluing might be a map from the interval to the circle.

It is called the identification function or the quotient function. It is best understood via quotient spaces.

See also Maps and homology.