This site is being phased out.
Open and closed sets
Redirect to:
Suppose the set of all neighborhoods $\gamma$ in $X$ is given. We define open sets as ones where every point has its own neighborhood:
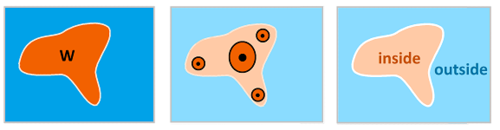
Definition. A subset $W$ of $X$ is called open (with respect to $\gamma$) if for any $x$ in $W$ there is a neighborhood $U$ ($\in \gamma$) of $x$ that lies entirely within $W$.
For example all "open" intervals, finite or infinite, are open in ${\bf R}$: $$(0,1), (0, \infty ), (- \infty ,0).$$
"Open" disks on the plane, and balls in the Euclidean space are also open.
Definition. A set is called closed if its complement is open.
For example all "closed" intervals, finite or infinite, are closed in ${\bf R}$: $$[0,1], [0, \infty ), (- \infty ,0].$$
"Closed" disks on the plane, and "closed" balls in the Euclidean space are also closed. Points too.
Some sets are neither closed nor open (unlike doors). Examples in in ${\bf R}$: $$[0,1),$$ $$P = \{ \frac{1}{n} \colon n=1,2, \ldots \}.$$
To see that the latter is neither (with respect to the standard Euclidean topology) consider two facts:
- $x=1$ does not have an interval around it that lies inside $P$;
- $x=0$ is in the complement of $P$ but it does not have an interval around it that lies inside in ${\bf R} \setminus P$.
However $P \cup \{0 \}$ is closed.
Exercise. Prove that if $U$ is open with respect to the disks it is also open with respect to the squares, and vice versa. Solution:
![]()
Theorem. The intersection of two open sets is open.
Proof. Rewrite the definition three times for each of the three sets involved, compare, then use (B2). More: ![]()
Theorem. The union of any collection of open sets is open.
Proof. Exercise. $\blacksquare$
To summarize...
Theorem. The set $\tau$ of all open sets satisfies the following conditions:
- (T1) $\emptyset, X \in \tau$;
- (T2) if $\alpha \subset \tau$ then $\cup \alpha \in \tau$;
- (T3) if $U,V \in \tau$ then $U \cap V \in \tau$.
Exercise. Prove (T1).
Definition. A collection $\tau$ that satisfies conditions (T1) - (T3) is called the topology of $X$ (with respect to the neighborhoods $\gamma$).
Corollary. The topology in ${\bf R}^2$ with respect to the disks is the same as the topology with respect to the squares.
For more details and examples see Neighborhoods and topologies.
Theorem. The union of two closed sets is open.
Proof. Rewrite the definition three times for each of the three sets involved, compare, then use (B2). $\blacksquare$
Theorem. The intersection of any collection of open sets is open.
Proof. Exercise. $\blacksquare$
To summarize...
Theorem. The set σ of all closed sets satisfies the following conditions:
- (T1') $\emptyset, X \in \sigma$;
- (T2') if $\alpha \subset \sigma$ then $\cap \alpha \in \sigma$;
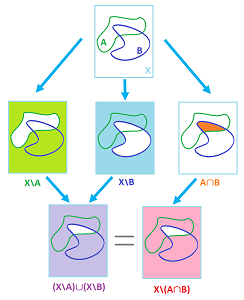
- (T3') if $P,Q \in \sigma$ then $P \cup Q \in \sigma$.
Proof. (T3') follows from (T3), illustrated below:
$\blacksquare$
From (T3) and (T3') it follows:
Corollary.
- The intersection of a finite number of open sets is open.
- The union of a finite number of closed sets is closed.
Proof. Exercise. $\blacksquare$
To see why the corollary can't be extended to infinite collections of sets consider these examples:
- $\cap \{( -\frac{1}{n}, \frac{1}{n}): n = 1,2, \ldots \} = \{0 \}$;
- $\cup \{[-1 + \frac{1}{n}, 1 - \frac{1}{n}] \colon n = 1,2, \ldots \} = (-1,1)$;
So, there is no (T3) for closed sets and no (T3') for open sets.
For more examples see Realizations of cubical complexes.