Cubical chain complex

Redirect to:

• Oriented chains

Suppose we have a cubical complex, which is used to represent geometric objects in a finite form. It is a list of "cells" combined with the information on how they are attached to each other.

Example. The cubical complex of the pixel at the origin is a list of cells of all dimensions:

• $ \{0 \} \times \{0 \}, \{1 \} \times \{0 \}, \{0 \} \times \{1 \}, \{1 \} \times \{1 \}, $
• $1: \{0 \} \times (0,1), (0,1) \times \{0 \}, (0,1) \times \{1 \}, \{1 \} \times (0,1), $
• $2: (0,1) \times (0,1).$

Now their boundaries:

• $\partial \{(0, 0) \} = 0, etc, $
• $\partial \{0 \} \times (0,1) = \{(0,0) \} + \{(0,1) \}, etc, $
• $\partial (0,1) \times (0,1) = (0,1) \times \{0 \} + \{0 \} \times (0,1) + (0,1) \times \{1 \} + \{1 \} \times (0,1).$

The right hand sides of these equations are chains. Chains are simply "sums" of cells. Important: $0$ is a chain too.

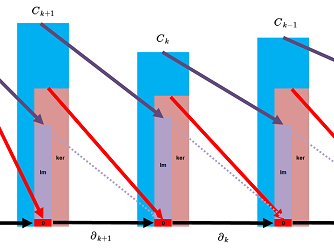
Given a cubical complex $K$, the set of all $k$-chains is called the chain complex $C_k(K)$ of $K$, or all together $C_*(K)$.

Now the boundary of a chain can be computed as the sum of the boundaries of the cells involved.

Definition. Given a chain $$s = a_1 + a_2 + ... + a_n,$$ where $a_1, a_2, \ldots, a_n$ are cells, the boundary $\partial s$ of $s$ is given by $$\partial s = \partial a_1 + \partial a_2 + ... + \partial a_n.$$

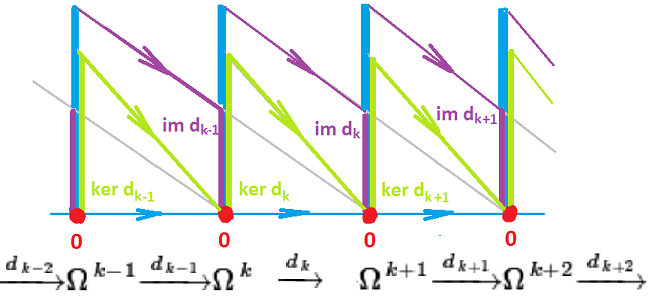
So the boundaries of $n$-cells are $(n-1)$-chains, and, moreover, the boundaries of $n$-chains are $(n-1)$-chains. Thus, the boundary is a linear operator $$\partial \colon C_{k}(K) → C_{k-1}(K)$$ and $$\partial \colon C_{*}(K) → C_{*}(K)$$ It is called the boundary operator.

Example. The boundary of the boundary of a $2$-cell: $$\begin{array}{} \partial \partial _k (n, n + 1) \times (m, m + 1) \\ = \partial ( (n, n + 1) \times \{m \} + \{n \} \times (m, m + 1) + (n, n + 1) \times \{m + 1 \} + \{n + 1 \} \times (m, m + 1) ) \\ {\rm (compute)} \\ = 0. \end{array}$$

Exercise. Check the computation above.

Theorem. $$\partial \partial = 0.$$

Exercise. Prove the theorem in this setting. Solution:

Exercise. Prove that $\partial \partial (3-cell) = 0$. Solution:

The chain complex then looks like this:

The above theorem is a counterpart if the Poincare Lemma and this is why it looks very similar to the cochain complex -- except unlike the exterior derivative operator $d$, the boundary operator $\partial$ decreases the dimension:

Chain complexes are used to compute homology of cubical complexes.