This site is being phased out.
Connected sum
Redirect to:
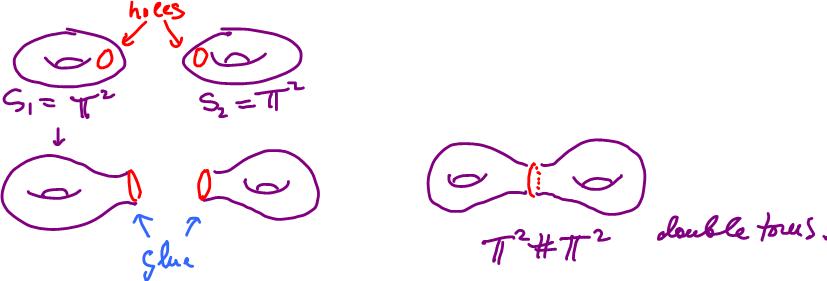
Any two surfaces can be attached to each other by punching holes in them and then gluing them together along these edges.
The result is called the connected sum $S_1 \# S_2$ of surfaces $S_1$, $S_2$.
For example, this is how you create the double torus by attaching two tori to each other in this fashion.
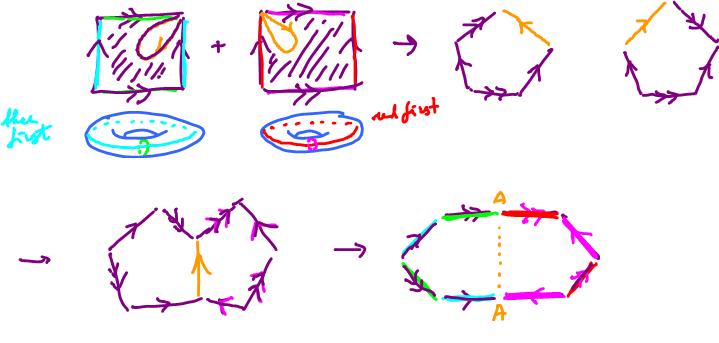
More precisely, one considers these diagrams:
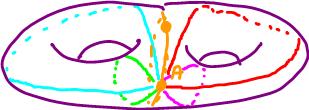
Then one can interpret the diagram by gluing along the edges:
These are the cuts:
Exercise. Prove $S \# {\bf S}^2 = S$.
Exercise. What is ${\bf P}$$^2 \# {\bf P}^2$?
Theorem (Classification of surfaces). (1) A compact connected surface is homeomorphic to
- the sphere ${\bf S}^2$, or
- the connected sum of $n$ tori ${\bf T}^2$, or
- the connected sum of $n$ projective planes ${\bf P}^2$.
(2) These options are not homeomorphic.
The options are: ${\bf S}^2, n{\bf T}^2, n{\bf P}^2$.
Exercise. Classify:
- ${\bf S}^2 \# {\bf S}^2,$
- ${\bf P}^2 \# {\bf K}^2,$
- ${\bf T}^2 \# {\bf K}^2,$
- ${\bf K}^2 \# {\bf K}^2.$
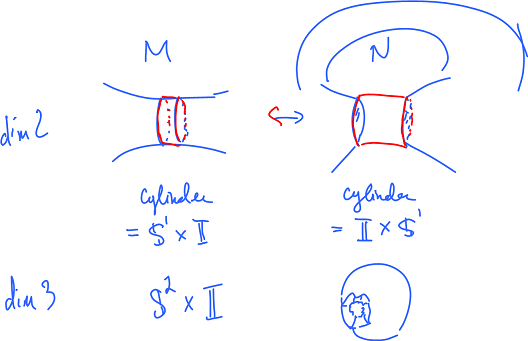
This is a particular case of surgery: