This site is being phased out.
Sub-pixel accuracy for distance measurement
Q: "The goal is to find the distance between two light emitters that are both within a single pixel. One will go dark after a period of time and the other will go dark after another period of time. ...we are looking to see if you see an issues in some of the techniques we are using or can propose better algorithms."
Papers:
- Myosin V Walks Hand-Over-Hand: Single Fluorophore Imaging with 1.5-nm Localization by Ahmet Yildiz, Joseph N. Forkey, Sean A. McKinney, Taekjip Ha, Yale E. Goldman, Paul R. Selvin, SCIENCE VOL 300 27 JUNE 2003.
- Single-molecule high-resolution imaging with photobleaching by Matthew P. Gordon, Taekjip Ha, and Paul R. Selvin, 6462–6465 PNAS, April 27, 2004, vol. 101, no. 17.
Let me summarize.
Problem:
- Given a few emitters going on and off, find their coordinates from a video.
Challenges:
- The emitters are blurred forming spikes.
- There is other noise.
- The spikes are just a few pixels in size.
- The sources are sometimes closer than the size of the pixel leading to overlapping spikes.
Main methods:
- Enhancing the images: smoothing and background removal.
- Averaging the corresponding spikes throughout the frames.
- Fitting a Gaussian to each spike, then the mean of this distribution is supposed to be the location of the emitter [2].
- MATLAB is used.
- A lot more is done...
Observations:
- Spikes are simply objects in gray scale images. The question is where to cut the spikes.
- Smoothing also smooths the spikes.
- Averaging the spikes affect the accuracy of the their coordinates. The reason is that the spikes switch on and off, merge, disappear. (It is a separate issue how to find out when it happens.) So, the spike is averaged with the noisy background.
- Instead of Gaussian fitting to find the distribution, it is better to use the data to find its mean and standard deviation, which produce a normal distribution if you need it. Taking the centroid is an alternative to finding the center of mass (i.e. the mean). The advantage of this approach is that it works (i.e., gives you the center of the emitter) even in the case the distribution isn't Gaussian such in the case of overlapping spikes.
- Gaussian fitting gives you the best normal curve to fit the data; the existence of a fit does not prove that the data is distributed normally. For that you need statistical methods. A problem is that this is such a small sample.
- Curve fitting the Gaussian to the histogram of the distances to evaluate the separations [2] assumes that the distribution is normal.
- Formula (1) in [1] has mismatched units.
The main issue however is this:
- Averaging the spikes obscures the fact that the coordinates of each spike varies from frame to frame.
How much do they vary? The answer will give you the best possible accuracy of the measurement.
Experiment 1:
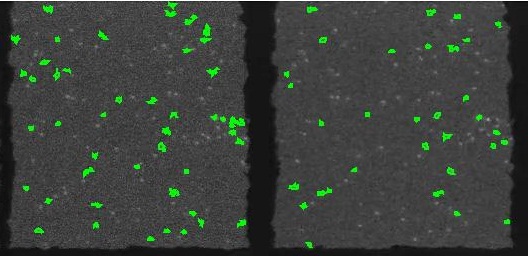
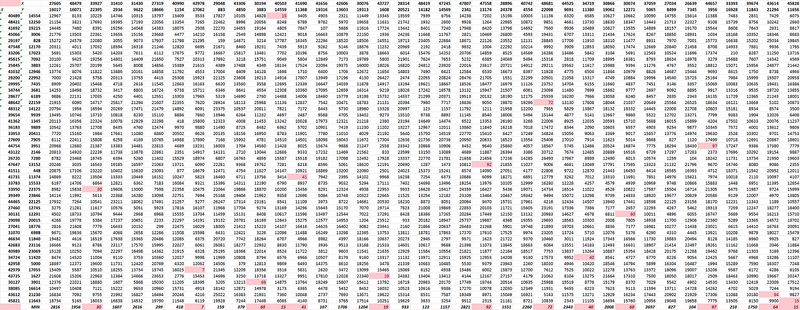
The goal was to test the approach in order to see of it's possible to track emitters from frame to frame and for that I used Pixcavator. I picked a couple of frames, fairly far apart from each other and converted them to bmp images. I analyzed each with Pixcavator with the same settings (15-50). The number of emitters detected was quite different but I was only interested in the ones easiest to track. I saved the lists of objects to Excel for both images. Then I put the coordinates (multiplied by 100) from the first image vertically and from the other horizontally (I had to transpose), and computed the distances between them in a large table. The entries with distance <100 are in red. These clearly correspond to the same emitters (not doubles) in these two frames. However, the distances are quite large:
0.30 0.55 0.70 0.60 0.40 0.36 0.94 0.56 0.72 0.83 0.29 0.30
pixels. So, the approach seems to work but the accuracy is low.
Experiment 2:
Instead of using the centroids of the spikes (as Pixcavator normally does), I used the centers of mass. The results are better. The distances are:
0.30 0.07 0.69 0.15 0.41 0.19 0.92 0.72 0.40 0.60 0.97 0.64 0.15
pixels.
See other examples of image analysis.