Selection votes

Social choice: the lottery of life

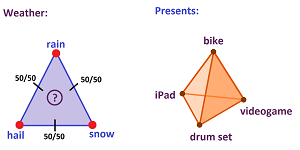
Suppose we face $n+1$ possible events or outcomes, $A_0, ...,A_n$. They are conveniently located at the vertices of an $n$-simplex $\sigma ^n=A_0...A_n$.

In addition to these “primary” events, we can also to consider their combinations. In what sense? These events are seen as mutually exclusive but all of them may come true. What happens is determined by the probabilities assigned to the primary events. These convex combinations of primary events are called lotteries, or, in the context of game theory, mixed strategies. The lotteries are conveniently represented by the points of the simplex $\sigma ^n$ and the barycentric coordinates of a point are the probabilities of the outcomes of the lottery. Then $\sigma ^n$ becomes the probability simplex.

Example. The midpoint between “rain” and “snow” represents the lottery when either is equally likely to appear while “hail” is impossible. The probabilities of the three events give the vector $(\tfrac{1}{2},\tfrac{1}{2},0)$ of barycentric coordinates of this point. $\square$

We next consider possible preferences of a person among these primary choices and, furthermore, among the lotteries.

The person's set of preferences is given by an order relation on the set of lotteries, i.e., the probability simplex $\sigma^n$. This means, as we know, that the following two axioms are satisfied:

• completeness: for any lotteries $x,y$, exactly one of the following holds:

$$x < y, \ y > x, \ \text{ or } y=x;$$

• transitivity: for any lotteries $x,y,z$, we have:

$$x \le y, \ y \le z \Longrightarrow x \le z.$$

Sometimes these preferences are expressed by a single function.

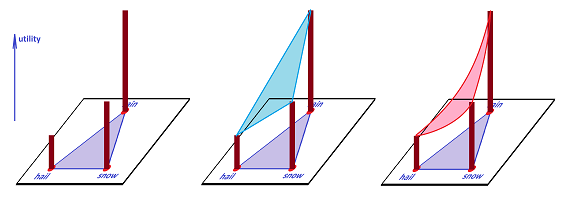
Definition. A utility of a given set of preferences is a function $$u:\sigma ^n\to {\bf R},$$ that satisfies: $$x < y \Longleftrightarrow u(x) < u(y).$$

Example. One may prefer: $$rain \ >\ snow\ >\ hail,$$ and define the utility function $u$ by assigning: $$u(r):=3, \quad u(s):=2, \quad u(h):=1.$$ Then, we may evaluate the lotteries by extending $u$ to the whole $2$-simplex, by linearity: $$u(t_1r+ t_2s+t_3h):=t_1\cdot 3+ t_2 \cdot 2+t_3 \cdot 1.$$ Of course, a circular preference, such as $$rain \ > \ snow \ > \ hail \ > \ rain,$$ doesn't have a corresponding utility function. $\hspace\fill\square$

Under certain special circumstances the preferences can be represented by a utility function of a very simple form -- a linear combination of the utilities of the primary outcomes: $$U(p_0, ...,p_n)= \displaystyle\sum_i p_iu_i,$$ where $u_0, ..., u_n$ are some numbers. This function is called the expected utility.

Of course, a person may have preferences that vary non-linearly but it is always assumed that the utility function is continuous.

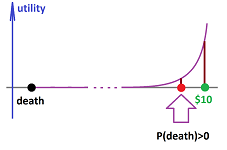
In the study of human behavior, this assumption may present a problem. Even though one would always choose $\$ 10$ over death, the continuity implies that, for a small enough probability $\alpha$, he would see a positive value in the following extreme lottery:

• death: probability $\alpha >0$; and
• $\$ 10$: probability $1-\alpha$.

Exercise. Show that, moreover, such a lottery (with death as a possible outcome) will have a higher utility than that of $\$ 1$, for a small enough $\alpha$.

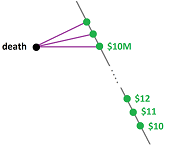
The reasons why we find this conclusion odd may be that, even though they are clearly comparable, death and $\$ 10$ seem incompatible! On the other hand, death and $\$ 10$ million may seem compatible to some people and these people would take part in such a lottery. To account for these observations, we should have an edge between “death” and $\$ 10$M but no edge between “death” and $\$ 10$:

Then, instead of a single simplex, the space of outcomes is a simplicial complex. The complex is meant to represent all possible or plausible lotteries. (Note that one can start with $\$ 10$ and continue gradually, in a compatible fashion, to worse and worse things until reaching death.)

Do we ever face a space of outcomes with a more complex topology, such as one with holes, voids, etc.?

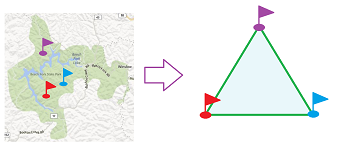
Let's recall the problem of social choice for two hikers: we are to develop a procedure for finding a fair compromise on the location of the camp on the shore of a lake. In the original statement of the problem, the choices of sites are arbitrary locations. Still, a simplicial interpretation can be justified too, as follows. Suppose there are three camp sites already set up on the shore of the lake and let's assume that they are the only ones available.

Either hiker has a preference location on the shore, but, for the record, he may have to make this choice by assigning an appropriate probability, or weight, to each camp site. For example, if the person's choice is located between camps $A$ and $B$ and twice as close to $A$ than to $B$, he may assign: $2/3$ to $A$, $1/3$ to $B$, and $0$ to $C$. That sets up a lottery for him. By allowing no more than two non-zero weights, we limit ourselves to the simplicial complex of the hollow triangle. (For the original problem, once the aggregation of the choices is completed and the compromise location is chosen, its coordinates are used for a lottery on the whole $2$-simplex.)

The expected utility exists under very natural restrictions, but only on the whole simplex! We state the following without proof.

Theorem (Von Neumann–Morgenstern Utility Theorem). Suppose two extra conditions are satisfied:

• continuity: if $x \le y \le z$, then there exists a probability $p\in [0,1]$ such that

$$px + (1-p)z = y;$$

• independence: if $x<y$ then for any $z$ and any $p\in (0,1]$,

$$px+(1-p)z < py+(1-p)z.$$ Then there is an expected utility.

Does an expected utility have to exist when some of the primary outcomes are incomparable?

What do we mean by that? Does a utility exist for the simplicial complex with no edge between “death” and $\$ 10$? The simplicial complex of the camp sites on the lake shore contains no $2$-face so that even though the pairs AB, BC, and AC are compatible and produce lotteries, the triple ABC does not. So, is there a utility on this hollow triangle?

We assume that the preferences satisfy the conditions of the theorem on each simplex $a$ of the complex $K$, as a partial order: $x<_ay$. We also assume that these partial orders are compatible in the sense that two orders on two simplices coincide on their intersection, which is also a simplex: $$x<_ay \Leftrightarrow x<_by, \ \forall a,b\in K, x,y \in a\cap b.$$ Then there is an expected utility $u_a:a\to {\bf R}$ for each of the simplices $a\in K$. Can those be patched together? In other words, is there $u:|K|\to {\bf R}$ with those of the simplices: $$u\Big|_a=u_a, \ \forall a\in K?$$

We use the fact that adding a constant and multiplying by another will create a new expected utility for the set of preferences.

Corollary. Suppose the conditions of the theorem are satisfied for each simplex of the simplicial complex $K$. Suppose also that these orders are compatible. Suppose the orders generate an acyclic directed graph on $K^{(1)}$. Then there is an expected utility for the whole $K$.

Proof. Every acyclic directed graph $G$ allows a topological sorting: $$(x,y)\in G \Leftrightarrow x<y.$$ The sorting is built as follows. (1) Start with a source $S$ and add it to top of the list. (2) Remove $s$ and all outgoing edges of $S$ from $G$. (3) Repeat. With the order of vertices found, apply the theorem to each $2$-simplex, $3$-simplex, etc. $\blacksquare$

To sum up, we have disallowed some lotteries/mixed strategies in order to prevent the participants from doing some silly things: betting $\$ 10$ against death or placing a camp in the middle of a lake. This decision has produced a space of choices with a possibly non-acyclic topology. This makes impossible some compromises or other desirable social arrangements.

From algebraic means to topological means

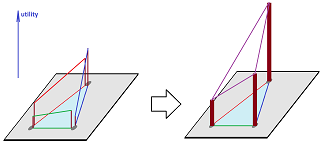
Definition. For a topological space $X$ and integer $m>1$, a map $f:X^m\to X$ is called a topological mean of degree $m$ on $X$ if $$f(s(u))=f(u),\ \forall u\in X^m,\ \forall s\in \mathcal{S}_m;$$ and $$f(x,x, ...,x)=x,\ \forall x \in X.$$

In 1943 Aumann states that the existence is a topological problem for arbitrary spaces; he solves it, however, for a few very special cases only. Thus the problem was open and well-known at the time. Eckmann decided to look at it from the viewpoint of algebraic topology in his paper published in 1954, more precisely, from the point of view of categories.

In order to transform the given topological mean into an algebraic mean he applied functors from topological spaces to groups (and continuous maps to homomorphisms). Below we have a commutative diagram of polyhedra and maps to be completed ($\delta $ is the diagonal map) by finding a map $f$ and, second, the same diagram with function ${\mathscr F}$, applied: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{cccccccccccc} & X\ & \ra{\delta} & X^m &&&& {\mathscr F}(X)\ & \ra{{\mathscr F}(\delta )=d} & {\mathscr F}(X^m) \\ &_{\operatorname{Id}} & \searrow & \ \quad \da{f=?} &&\ra{\quad {\mathscr F} \quad} && & _{\operatorname{Id}}\searrow & \ \ \ \da{ {\mathscr F}(f) =g=?} \\ & & & X&&&& & & {\mathscr F}(X) \end{array} $$

At this point, we observe that the non-triviality of these groups could make it impossible to complete the latter and, therefore, the former diagram. This clearly works when the functor preserves products; i.e., the product of $n$ copies of space $X$ becomes the product of $n$ copies of the corresponding group: $$ {\mathscr F} (X^n)={\mathscr F} (X)^n.$$

We also use the following two facts:

Proposition.

• $d:={\mathscr F}(\delta):{\mathscr F}(X)\to {\mathscr F}(X)^m$ is the diagonal function.
• $g:={\mathscr F}(f):{\mathscr F}(X)^m\to {\mathscr F}(X)$ is symmetric.

As a result, the last, algebraic, diagram becomes identical to the one in the Tally Theorem, which leads to a contradiction.

Each homotopy group is such a functor. But what about homology?

The “naive product formula” for homology implies the following:

Proposition. Suppose $X$ is path-connected and $p>0$. Suppose also:

• $H_k(X)=0,\ k=1,2,...,p-1;$
• $G:=H_p(X)\ne 0.$

Then, $$H_p(X^m)=G^m.$$

We can choose then ${\mathscr F}:=H_p$. The main result is the following:

Impossibility Theorem II. (1) Suppose $X$ is a path-connected polyhedron. If there is a topological mean on $X$ then $X$ has only trivial homotopy groups. (2) Suppose $X$ is a path-connected polyhedron and has torsion-free integral homology. If there is a topological mean on $X$ then $X$ is acyclic.

Example (yeast colonies). The development of an yeast colony is cyclic: each stage is just a point on the circle $W={\bf S}^1$. If two such colonies are to merge, what is the stage of the new one? The answer should be given by a function $f:{\bf S}^1\times {\bf S}^1\to {\bf S}^1$ that satisfies the axioms of symmetry and diagonality. Then the impossibility theorem indicates the discontinuous nature of such a merge. $\square$

Compromise for two

Let's imagine two hikers who are about to go into the woods and they need to decide where to set up their camp. Their preferred places don't match and we need to develop a procedure for them to find a fair compromise:

We are not speaking of a one-time compromise but a compromise-making procedure. The reason is that we want to solve the problem once and for all -- in case they decide to take a trip again.

The solution may be simple: take the middle point between the two locations, if possible:

Because of the last part, the answer depends on the geometry (and the topology!) of the set of possible choices, the forest.

So, this is what we have so far:

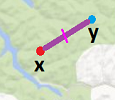
• the forest: a closed subset $W$ of ${\bf R}^2$,
• the location chosen by the first hiker: $x\in W$, and
• the location chosen by the second hiker: $y\in W$. $\\$

We need to find

• a compromise location $C\in W$, $\\$

and not just once, for these particular $x,y$, but for all possible pairs $x,y \in W$. It is then a function, which we will call the choice function, $$f:W\times W\to W,$$ that we are after.

Now, whenever $W$ allows, we choose the mid-point function: $$f(x,y):=\tfrac{1}{2}x+\tfrac{1}{2}y.$$ Such a choice is, of course, always possible when $W$ is convex. When it's not, the answer is unclear. We then want to understand when this problem does have a solution, a choice function $f$. The answer will depend on the set $W$.

But first, let's make sure that $f$ that we find will make sense as the answer in this particular situation.

First, the interests of both hikers should be taken into account equally. Certainly, a dictatorship of either one of the hikers can't be allowed: $$f(x,y)=x,\ \forall x,y.$$

We accomplish this by requiring that, if the two flip their preferences, the result will remain unchanged. Traditionally, this condition is called “anonymity”.

Anonymity Axiom (Symmetry): The choice function is symmetric: $$f(x,y)=f(y,x),\ \forall x\in W.$$

Unfortunately, a constant function $$f(x,y):=P,\ \forall x,y,$$ for some $P\in W$, demonstrates a kind of dictatorship (by a third party?) that passes the test of the Anonymity Axiom. This is why we also need to ensure that these two persons are the ones and the only ones who decide. We require that, if the two choices happen to coincide, that's the choice that will be made. Traditionally, this condition is called “unanimity”.

Unanimity Axiom (Diagonality): The choice function restricted to the diagonal is the identity: $$f(x,x)=x,\ \forall x\in W.$$

Naturally, we will require $f$ to be continuous. The justification is the same as always: a small change in the input -- the choice of one of the two hikers -- should produce only a small change in the output -- the compromise choice. As another way to look at this, the error (caused by limited accuracy) of the evaluation of the preferences won't dramatically change the result. Traditionally, this condition is called “stability”.

Stability Axiom (Continuity): The choice function $f:W\times W\to W$, where $W\times W \subset {\bf R}^4$, is continuous.

Finally, the social choice problem is:

Is there a function $f:W\times W\to W$ that satisfies these three axioms?

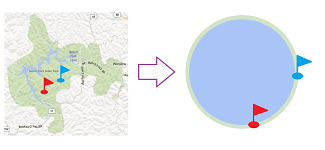
A positive answer won't tell us a lot. Consider how, when $W$ is homeomorphic to a convex set $Q$, we solve the problem for $Q$ and then bring the solution back to $W$:

Specifically, if $h:W\to Q$ is such a homeomorphism, our solution is $$f(x,y)=h^{-1}\Big( \tfrac{1}{2}h(x)+\tfrac{1}{2}h(y) \Big).$$ The solution is fair as it doesn't favor one hiker over the other, but would they be happy with it? As all the geometry of $Q$ is lost in $W$, such a “compromise” might be far away from the choices of either of the hikers.

We try to keep the constraints on $f$ as broad as possible and try to investigate what constraints on the topology of $W$ will make it possible that $f$ does exist. The example of the mid-point solution above already suggests that $W$ might have to be acyclic.

First, does $W$ have to be path-connected? In real life, the two persons may choose two different forests and there can be no fair compromise. The unfairness is seen from the fact that, even though the two hikers are treated equally, the two forests aren't (as if a third person chose a candidate ahead of time).

Next, does $W$ have to be simply connected? In practical terms, is it always possible to find a fair compromise between the two choices when there is a lake in the middle of the forest? To keep things simple, let's reduce the problem to the following:

• the hikers need to decide on a camping location on the shore of a circular lake:

When the two choices are close to each other, the solution can still be chosen to be the mid-point (along the arch). But what if they choose two diametrically opposite points, $x=-y$? Then there are two mid-points. Which one do we choose for $f(x,-x)$? A possible solution is to choose the one, say, clock-wise from first to second but that would violate the symmetry requirement.

We already know that some obvious solutions fail.

Let's observe that the diagonal of $W\times W$, $$\Delta (W):=\{(x,y)\in W\times W:\ x=y\} ,$$ is copied to $W$ by $f$.

Define the diagonal map $\delta:W\to W\times W$ by $\delta (x)=(x,x)$ (its image is the diagonal $\Delta (W)$ of $W$). Then, we can also interpret the axiom as the commutativity of this diagram: $$ \newcommand{\ra}[1]{\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{llccl} & W & \ra{\delta} & W\times W\\ & & _{\operatorname{Id}} \searrow & \da{f} \\ & & & W \end{array} $$

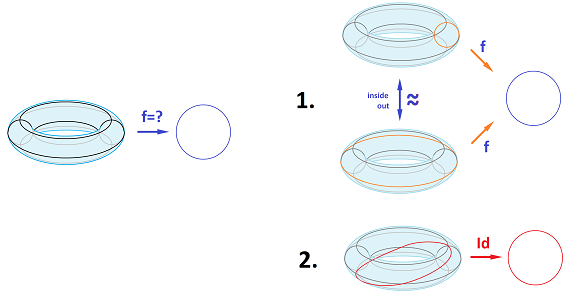
For the case of a lake, the choice space is a circle: $$W={\bf S}^1.$$ Then we recognize the product $W\times W = {\bf S}^1\times{\bf S}^1$ as the torus and its diagonal as just another circle:

Let's translate this topological problem into an algebraic one via homology.

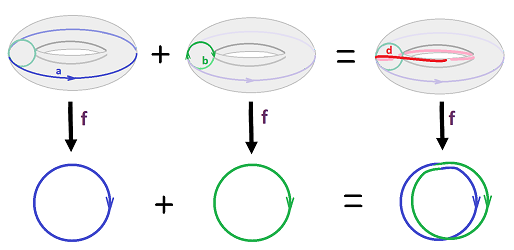
We know that $f$, if it exists, induces a homomorphism $$[f_1]:H_1({\bf S}^1)\to H_1({\bf S}^1)$$ on the homology groups: $$H_1({\bf S}^1)={\bf Z},\ H_1({\bf S}^1 \times {\bf S}^1)={\bf Z} \oplus {\bf Z}.$$ The problem then becomes: is there a homomorphism $$g:{\bf Z}\oplus {\bf Z}\to {\bf Z},$$ whether it comes from some simplicial map $f$ or not, that satisfies

• 1. $g(x,y)=g(y,x)$, and
• 2. $g(x,x)=x?$

The mathematical version of the problem and the two conditions are illustrated below:

Indeed, the image of the diagonal appears to be the double not the identity.

Let's restate these two problems in terms of commutative diagrams. Now the problem becomes, is it possible to complete this commutative diagram of simplicial complexes and simplicial maps, with some $f$? $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{ccccccc} & {\bf S}^1 & \ra{\delta} & {\bf S}^1 \times {\bf S}^1 \\ & _{\operatorname{Id}} & \searrow & \ \ \ \da{f=?} \\ & & & {\bf S}^1 \end{array}$$ The diagonal arrow is the identity according to the second condition. Applying homology to the above diagram yields a commutative diagram of groups and homomorphisms: $$ \newcommand{\ra}[1]{\!\!\!\!\!\!\!\xrightarrow{\quad#1\quad}\!\!\!\!\!} \newcommand{\da}[1]{\left\downarrow{\scriptstyle#1}\vphantom{\displaystyle\int_0^1}\right.} % \begin{array}{rcccccc} {\bf Z}\ & \ra{\delta _*=[1,1]^T} & {\bf Z} \oplus {\bf Z} \\ & _{\operatorname{Id}} \searrow &\ \ \ \ \da{g=?} \\ & & {\bf Z} \end{array} $$ The problem becomes, is it possible to complete this diagram, with some $g$? This is how the final contradiction is illustrated:

Other:

• the two hikers are to choose the time of the day to leave (repetitively);
• they are to choose the way to hang their hammock in the camp;
• they stopped in the middle of the forest and has to decide on the direction to follow.

Political creeds

This is a more general setup. There are $m$ voters, or agents, making their selections:

• the space of choices is a simplicial complex $W$;
• the choice made by the $k$th voter is a vertex $A$ in $W$. $\\$

Then a solution to the social choice problem is a compromise-producing rule, i.e., a function that converts the $m$ choices into one: $$f:(A_1, ...,A_m) \mapsto B,$$ where $ A_1, ...,A_m$, and $B$ are vertices in $K$, that satisfies the following three conditions:

• Continuity (Stability Axiom): The function $f:W^m \to W$ generated by its values on the vertices is a simplicial map. $\\$
• Symmetry (Anonymity Axiom): The function is symmetric; i.e.,

$$fs=f,\ \forall s\in S_m.$$

• Diagonality (Unanimity Axiom): The function restricted to the diagonal of $W^m$ is the identity; i.e.,

$$f\delta = \operatorname{Id}.$$

Typically, the political spectrum is understood as just left vs. right. Is there a way to see it as something with a non-acyclic topology?

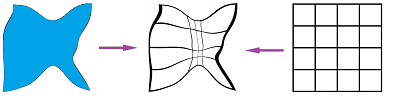
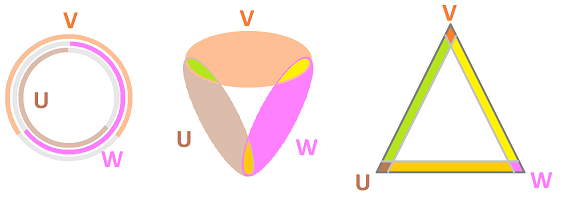
We utilize a common method of assigning topology to a set of data.

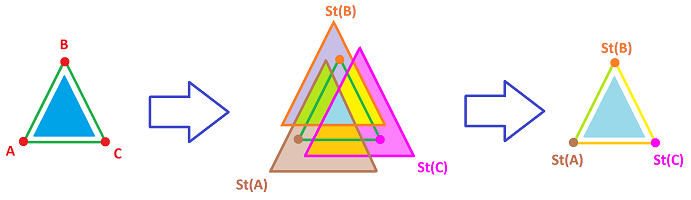
Now, we construct a simplicial complex from this open cover. The sets become the vertices and the intersections become the edges. We let $$L^{(0)}:= \{U,V,W \}.$$ These are the vertices of complex $L$. The $1$-simplices of $L$ come from the following rule: for every pair $G,H\in \gamma$, $$GH\in K \Longleftrightarrow G \cap H \ne \emptyset.$$ Further, the $2$-simplices of $L$ come from the following rule: for every triple $G,H,J\in \gamma$, $$GHJ\in K \Longleftrightarrow G \cap H \cap J\ne \emptyset.$$ There aren't any. The result is the circle ${\bf S}^1$.

This construction applied to a triangle is illustrated below:

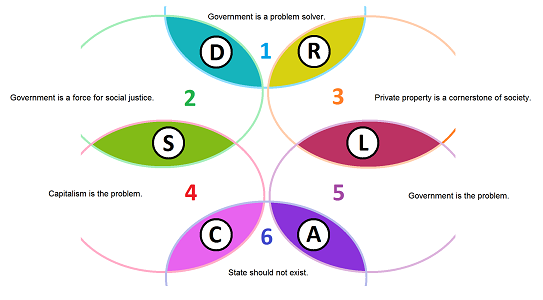
The six statements below are meant to represent an open cover of the political spectrum (in the US). In other words, we assume that everyone supports at least one of these statements:

• 1. Government is a problem solver.
• 2. Government is a force for social justice.
• 3. Private property is a cornerstone of society.
• 4. Capitalism is the problem.
• 5. Government is the problem.
• 6. State should not exist. $\\$

We call the sets of individuals supporting these statements $U_1, ...,U_6$ respectively. We now assign letters to the intersections of these sets. This way, we classify all individuals based on which statements they support under the assumption that no-one supports more than two:

• 1 and 2: $D:=U_1\cap U_2$,
• 1 and 3: $R:=U_1\cap U_3$,
• 2 and 4: $S:=U_2\cap U_4$,
• 3 and 5: $L:=U_3\cap U_5$,
• 4 and 6: $C:=U_4\cap U_6$,
• 5 and 6: $A:=U_5\cap U_6$.

Keep in mind that only the adjacency is represented in the complex and only the adjacency is illustrated; none of these concepts apply: “left-right”, “close-far”, “between”, “opposite”, or “extreme”:

The theorem above then claims that, if these issues are put to the vote, there can be no electoral system that would always produce a fair compromise, whether it is an idea or an individual.

A similar analysis shows that a compromise on colors may also be impossible -- without the gray:

In an attempt to resolve this “paradox”, we will allow choices that are more complex than just a single location or outcome: ratings. The topology of the space of choices will no longer be a problem.