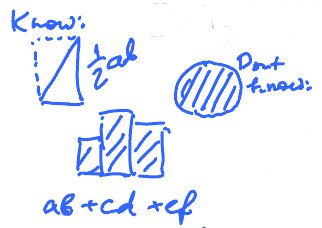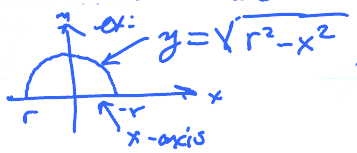This site is being phased out.
Preview of calculus: part 1
This is a part of Calculus 1: course.
There are two main problems in Calculus:
- Tangent Problem
- Area Problem
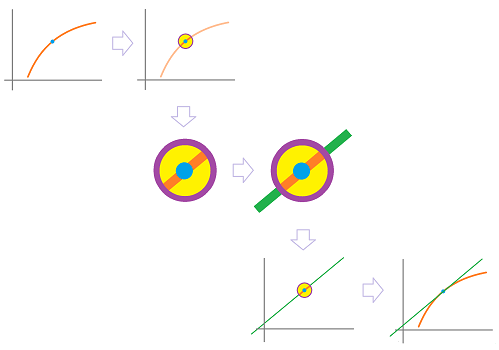
Tangent Problem
The word "tangent" means touch.
- Question
- What is the best way to describe the curve close to A?
- Answer
- We use a tangent line.
Why? The tangent line touches the point A and no where else in the curve. If we zoom in, they virtually merge.
One motivation comes from the study of motion.
Example 1:
- Question
- Where do the lights of a car traveling on a curvy road point?
- Answer
- The direction the lights point is a "tangent" to the road's curvature.
Example 2:
- Question
- Where would a rock released from a sling go (view from above)?
- Answer
- The rock's path is a straight line and we can measure its position.
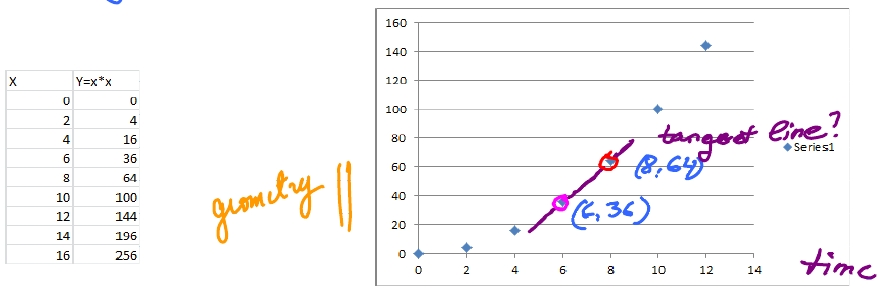
In real life, the position is given by DATA.
We measure the "rate of change" by measuring the slope of the line from one point to the next. From the graph above, this is the change in y over the change in x.
change in y = \(64 - 36 \)
change in x = \(8 - 6 \)
slope = \( \dfrac{\text{rise}}{\text{run}} = \dfrac{64-36}{8-6} = \dfrac{28}{2} = 14 \)
Continuous Curves
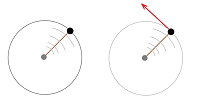
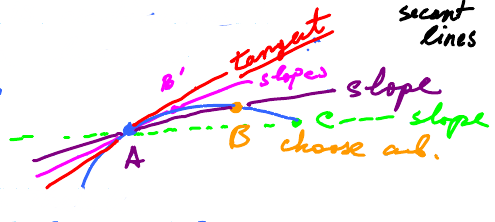
The rate of change of y with respect to x seems clear for discrete data but what if the change is continuous? We can't apply this algebra because there is no "next" point. When we draw secant lines, they cut the curve at various points. Ideally, we want to choose a line that just cuts one point on the curve; the tangent line.
We see that the line AB is better than AC and the closer our next point is to A, the better. But we can't have \( B = A \) as straight lines are defined by two points. Instead, we keep making the distance between \(A\) and \(B\) smaller.
This process is called 'limit and it's the essence Calculus.
What is this about?
To finish this process, we consider what the slope of the line would be as the limit of \( B - A \) approaches zero. This is called the derivative of \(AB\) and is the slope of the tangent line.
To illustrate the notion of limits, consider the sequence of numbers.
$$ 1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \ldots $$
Each step, the fraction gets smaller and smaller until it approaches an infinitesimal limit.
Area Problem
What is the area of a cardioid? and ellipse? or a circle?
You know that the area of a circle is \( a = \pi r^{2} \). But the real question is: What is the area? Do we understand it?
One thing we do know. The area of a rectangle \( a \times b\) is \( a b\). Further, triangles are the union of two rectangles. But what are the areas of curved objects?
To try to understand and compute these area, we approximate the curved areas by filling them with increasing number of rectangles or triangles and increasing the number of sides with each step. We can then calculate the area by calculating the area at each step and then taking the "limit".
The use of triangles makes the problem of determining the area more difficult than rectangles. For example, we can represent a circle using cartesian coordinates and represent it as the equation
$$ y = \sqrt{r^{2} - x^{2}} $$
where \( r \) is the radius and \( x \) is a point on the x-axis.
Then
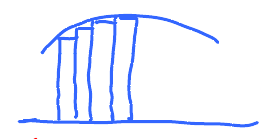
We can approximate the area under the graph through the use of rectangles, where the area under the graph \( \approx \) the sum of the areas of the rectangles.
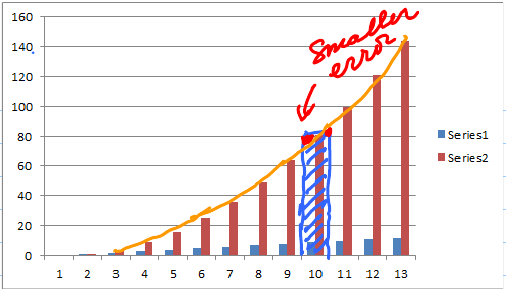
We find the total area under the curve by adding the areas of all the rectangles. We can improve accuracy by using thinner rectangles.
This time, the width of the rectangle is 1, then we have more rectangles to use and can reduce the error in our calculations. If we keep reducing the width to infinitesimal amounts and use an "infinite" number of rectangles, we can make the error disappear. This is what calculus is about.
Functions
Functions come from many sources and can be expressed in different forms.
- Algebraic Formula
- This can be represented by \( y = x^{2} \).
- Numerical Representation
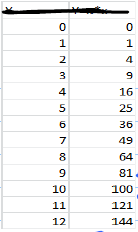
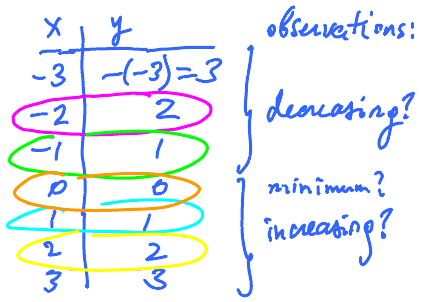
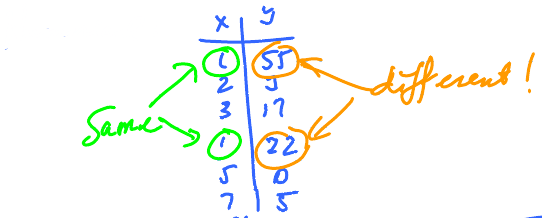
- This can be represented by the data in the table. These data in the table represents the same function above but, as we can see, there are gaps in the data. We can't tell, for example, what \( (1.5)^{2} \) is or even what \( (100)^{2} \) is.
Our algebraic representation is complete but the numerical representation listed in the table is not. (It always will be).
Q: Why isn't it complete?
The differences lie in the fact that one is a finite representation while the other is not. The numerical representation is limited by our ability to acquire data or to calculate it whereas the algebraic representation represents all possible numbers we can use.
Advantages of Numerical Representation
- Static, it has been calculated for you
- You can see patterns:
- If \( x \) is increasing, then \( y \) is increasing.
- If \( x \) grows faster, \( y \) also grows faster.
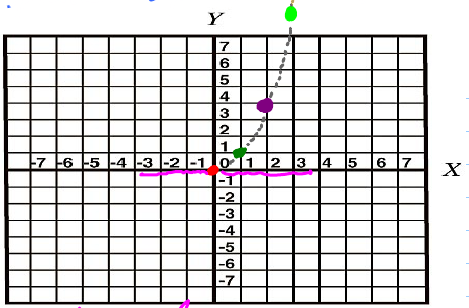
- We can use the data to plot points, which leads us to the graphical representation.
Graphical Representation
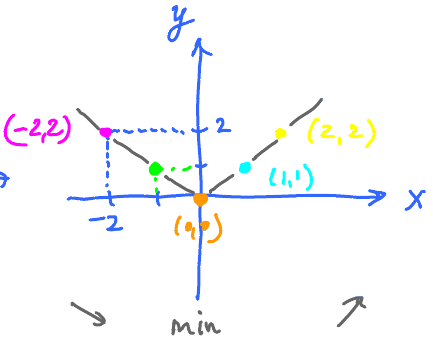
The graph above suggests that there is a tangent line at \( x = 0 \). Here the slope is horizontal or equal to zero.
Verbal Representation
The verbal representation contains no algebra. Rather it is more of an algorithm that tells us how to get a certain output given a certain input.
- Question
- How do we get from \( x \) to \( y \)?
- Answer
- Let \( y \) be equal to the square of \( x \) or \( x \) times \( x \).
This also gives us compete information about the function.
Example 3:
\( \dfrac{x^{2} + 1}{x^{2} -1} \)
- Step 1
- Multiply \( x \) by itself, call it \( y \).
- Step 2
- Add 1 to \( y \), call it \( z \).
- Step 3
- Subtract 1 from \( y \), call it \( u \).
- Step 4
- Divide \( z \) by \( u \).
This "verbal" representation can be used as the algorithm for a computer program.
In this case, \( x \) is the input, it passes through a "black box" and out comes \( y \). But we must be careful. If the denominator is zero, or rather \( x = 1 \), what happens? The function "explodes"!
Example 4:
\( y = f(x) = |x| \). Given an input of \( x \), describe a procedure for computing this function.
- Step 1
- Determine the sign, \( S \), of \( x \). If \( x \geq 0 \), then \( S = 1 \) else \(S = -1 \).
- Step 2
- Multiply \( S \) by \( x \).
- If \( x = 5 \), then \( S = 1 \).
- So $$ y = S \times x = 1 \times 5 = 5 $$ Here we see that \( x \) is positive. Thus \( S = 1 \).
- If \( x = -5 \), then \( S = -1 \).
- So $$ y = S \times x = -1 \times -5 = 5 $$ Here we see that \( x \) is negative. Thus \( S = -1 \).
- If \( x = 0 \), then \( S = 1 \).
- So $$ y = S \times x = 0 \times 1 = 0 $$ Here we see that \( x \) is neither negative nor positive but we set \( S = 1 \).
We can express this numerically...
We need more points to be sure of the trends.
Or graphically:
- Definition
- A function is a rule or procedure that assigns any number in a set \( D \), called the Domain, to one number in a set \( E \).
What does this definition mean?
- Any \( x \) in \( D \) has a counterpart in \( E \), and
- there is only one such counterpart.
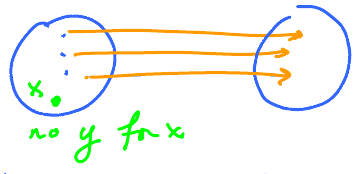
Not a function
Algebraically, plug \( x \) into the formula and see if it works.
Example: $$ f(x) = \frac{1}{x} $$
for \( x = 0 \).
It does not work as \( \frac{1}{0} \) is undefined.
Fact.
\( \dfrac{1}{x} \) is defined \( \forall x \neq 0 \). So, we can choose the domain to be all these numbers.
$$D = ( - \infty, 0 ) \cup ( 0, +\infty) $$
What about \( D_{1} = (0, \infty ) \)? it works too.
Example:
\( f(x) = \dfrac{1}{x} \), domain, \(D_{2} = [1,2] \)
The largest possible domain is called the natural domain.
Example:
\( f(x) = \dfrac{x^{2} + 1}{x^{2} - 1} \), find the domain.
There are some "problematic" algebraic operations:
- division (possibly by 0),
- square root (pf possibly negative numbers),
- 4, 6 roots (similar),
- tangents.
Solutions:
Don't divide by zero! So we need to ensure that the input \( x \) doesn't produce a 0 in the denominator.
Solve \( x^{2} - 1 = 0 \).
We see that \( x^{2} = 1 \). Thus \( x = -1\) and \( x = + 1\).
The function is defined by all values except \( \pm 1 \) or \( D = ( \infty, -1 ) \cup (-1 , 1) \cup ( 1, \infty) \).
Rule that defines functions
There is only one \( y \) for each \( x \).
Fact. The rule might fail for each of the four representations of \( f \).
Algebraic
Q: Is there an ambiguity in the formula?
Yes! As \( x = \pm 1 \).
Numerical
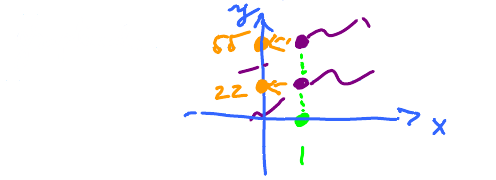
Graphical
So, this is not a function as there are two points above the same \( x \).
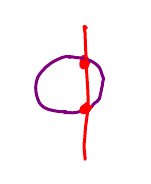
This is the vertical line test. Every vertical line crosses the graph at one point or less.
Algorithmic
- Step 1: ...
- ...
- ...
- Step 50: Add today's date to \( X \).
- ...
- ...
- Step 100: ...
$$\begin{aligned} x = 10 \Longrightarrow y & = 20 \\ y & = 21 \\ y & = 22 \end{aligned} $$
We can only deal with functions with single variables and inputs.