This site is being phased out.
Precalculus exercises
Contents
Algebra etc.
- Solve the quadratic equation $x^{2}+2x+10=0$ and represent the answer in the standard form $a+bi$, where $a$ and $b$ are real numbers.
- Solve the following equation: $\sqrt{x^2-7}-3=0$.
- Solve the following equation: $\left( x^2-7 \right)^3 -8=0$.
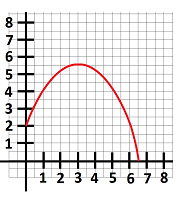
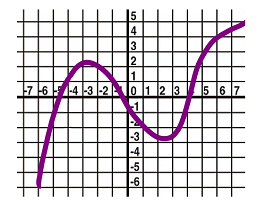
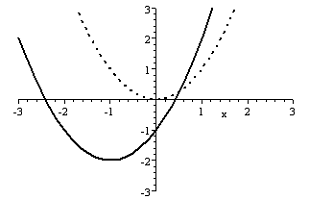
- Consider the parabola below. Find its vertex, its axis of symmetry, and its maximum or minimum.
- Find the exact values of the $x$-coordinates of the intersections between the parabola and the line below:
- There are $125$ sheep and $5$ dogs in a flock. How old is the shepherd?
- Let $h(x)=x^2+3x-10$. Find the $x$- and $y$-intercepts and sketch the graph of the function.
- Find an equation the solutions of which are $1$ and $2$.
Coordinate system
- Find the equation of the line passing through the points $(-1,1)$ and $(-1,5)$.
- What is the distance from the center of the circle $(x-1)^2+(y+3)^2=5$ to the origin?
- What is the distance from the the circle $x^2+(y+3)^2=2$ to the origin?
- Find the equation of the circle centered at $(-1,-1)$ and passing through the point $(-1,1)$.
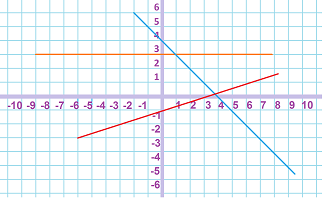
- Three straight lines are shown below. Find their slopes:
- Three straight lines are shown below. Find their equations:
Linear algebra
- Set up, but do not solve, a system of linear equations for the following problem: “Suppose your portfolio is worth $\$ 1,000,000$ and it consists of two stocks $A$ and $B$. The stocks are priced as follows: $A$ $\$2.1$ per share, $B$ $\$1.5$ per share. Suppose also that you have twice as much of stock $A$ than $B$. How much of each do you have?”
- In an effort to find the point in which the lines $ 2x -y=2 $ and $-4x+2y=1$ intersect, a student multiplied the first one by $2$ and then added the result to the second. He got $0=5$. Explain the result.
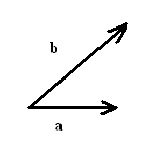
- Vectors $A$ and $B$ are given below. Copy the picture and illustrate graphically: (a) $A+B$, (b) $A-B$, (c) $||A||$.
- Find the angle between the vectors $<1,1>$ and $<1,2>$. Don't simplify.
- Solve the system of linear equations:
$$\left\{\begin{array}{lll} x&-y&=-1,\\ 2x&+y&=0.\\ \end{array}\right.$$
Polynomials
- Find the line passing through the point $(-1,2)$ and perpendicular to the line $y=-x-2016.$
- Suppose $f$ is a polynomial of degree $55$ and its leading term is $-1$. Describe the long term behavior of this function.
- For the polynomial $f(x)=-2x^2(x+2)^2(x^2+1)$, find its $x$-intercepts.
- Find a formula for a polynomial with these roots: $1$, $2$, and $3$.
- Find the equation satisfied by all points that lie $2$ units away from the point $(-1,-2)$ and by no other points.
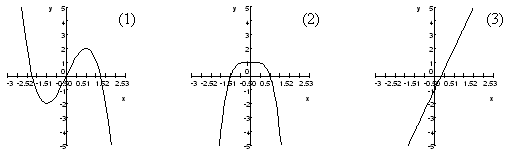
- For the polynomials graphed below, find the following:
$$\begin{array}{r|lll} &1&2&3\\ \hline \text{the smallest possible degree }&\\ \text{the sign of the leading coefficient }&\\ \text{the degree is odd/even } \end{array}$$
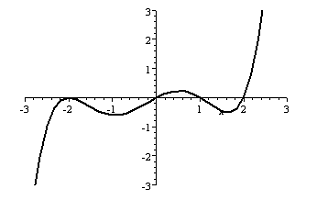
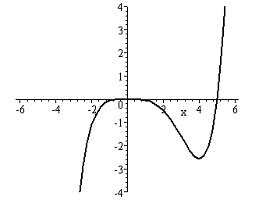
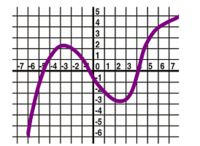
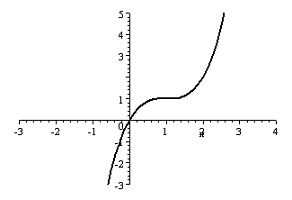
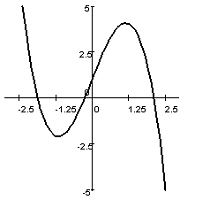
- Find a possible formula for the function plotted below:
- Find a possible formula for the function plotted below:
- For the polynomial $f(x)=-2x(x-2)^2(x+1)^3$, find its $x$-intercepts and its large scale behavior, i.e., $f(x)\to ?$ as $x\to \pm \infty$.
- Given $f(x)=-(x-3)^{4}(x+1)^{3}$. Find the leading term and use it to describe the long term behavior of the function.
- (a) Solve the equation $(x^2+1)(x+1)(x-1)=0$. (b) Solve the inequality $(x^2+1)(x+1)(x-1)>0$.
Functions
- The perimeter of a rectangle is $10$ feet. (a) Express the area of the rectangle in terms of its width. (b) Find the minimal possible area. (c) Find the maximal possible area.
- The area of a rectangle is $100$ sq. feet. (a) Express the perimeter of the rectangle in terms of its width. (b) Find the minimal possible perimeter. (c) Find the maximal possible perimeter.
- The graph of the function $y=f(x)$ is given below. (a) Find such a $y$ that the point $(2,y)$ belongs to the graph. (b) Find such an $x$ that the point $(x,3)$ belongs to the graph. (b) Find such an $x$ that the point $(x,x)$ belongs to the graph. Show your drawing.
- Make a hand-drawn sketch of the graph of the function:
$$f(x)= \begin{cases} -3 &\text{ if } x<0\\ x^2 &\text{ if } 0\le x<1\\ x &\text{ if } x>1 \end{cases}$$
- Find the implied domains of the functions given by:
$$\text{(a) } \frac{x+1}{\sqrt{x^2-1}};\ \text{(b) }\sqrt[4]{x+1}.$$
- Find the implied domain of the function given by:
$$\frac{1}{(x-1)(x^2+1)}.$$
- Find the implied domain of the function given by:
$$\frac{1}{\sqrt{x+1}}.$$
- Find the implied domain of the function given by:
$$(x-1)(x^2+1)2^x.$$
- Finish the sentence: “If a function fails the horizontal line test, then...”
- Restate (but do not solve) the following problem algebraically: “What are the dimensions of the rectangle with the smallest possible perimeter and area fixed at $100$?”
- A sketch of the graph of a function $f$ and its table of values are given below. Complete the table:
$$\begin{array}{r|ll} x&0& &3& &1\\ \hline y&2&4& &5& \end{array}$$
- Plot the graph of the function $y=f(x)$, where $x$ is the income (in thousands of dollars) and $f(x)$ is the tax bill (in thousands of dollars) for the income of $x$, which is computed as follows: no tax on the first $\$ 10,000$, then $5\%$ for the next $\$ 10,000$, and $10\%$ for the rest of the income.
- Plot the graph of the function $y=f(x)$, where $x$ is time in hours and $y=f(x)$ is the parking fee over $x$ hours, which is computed as follows: free for the first hour, then $\$1$ per every full hour for the next $3$ hours, and a flat fee of $\$5$ for anything longer.
- Explain the difference between these two functions:
$$\sqrt{\frac{x-1}{x+1}}\text{ and } \frac{\sqrt{x-1}}{\sqrt{x+1}}.$$
Features of graphs
- Is the function below even, odd, or neither?
$$f(x)=\frac{x}{e^x-1}+\frac{1}{2}x-1$$
- Give an example of an even function, an odd function, and a function that's neither. Provide formulas.
- Test whether the following three functions are even, odd, or nether: (a) $f(x)=x^3+1$, (b) the function the graph of which is a parabola shifted one unit up, (c) the function with this graph:
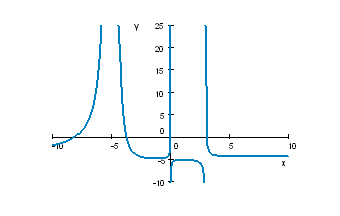
- Find horizontal asymptotes of these functions:
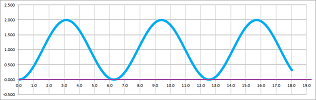
- Is $\sin x/2$ a periodic function? If it is, find its period. You have to justify your conclusion algebraically.
- Is $\sin x+\cos \pi x$ a periodic function? If it is, find its period. You have to justify your conclusion algebraically.
- Is $\sin x+\sin 2x$ a periodic function? If it is, find its period. You have to justify your conclusion algebraically.
- (a) State the definition of a periodic function. (b) Give an example of a periodic polynomial.
- Prove, from the definition, that the function $f(x)=x^2+1$ is increasing for $x>0$.
- The graph of a function $f(x)$ is given below. (a) Find $f(-4)$, $f(0)$, and $f(4)$. (b) Find such an $x$ that $f(x)=2$. (c) Is the function one-to-one?
- A sketch of the graph of a function $f$ is given below. Describe its behavior the function using words “decreasing” and “increasing”.
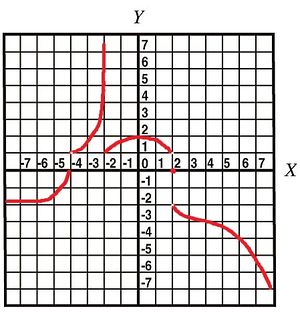
- The graph of the function $y=f(x)$ is given below. (1) Find its domain. (2) Determine intervals on which the function is decreasing or increasing. (3) Provide $x$-coordinates of its relative maxima and minima. (4) Find its asymptotes.
Compositions
- Find the composition $h(x)=(g\circ f)(x)$ of the functions $y=f(x)=x^{2}-1$ and $g(y)=3y-1.$ Evaluate $h(1)$.
- Represent the function $h(x)=2\sin^3x+\sin x+5$ as the composition of two functions one of which is trigonometric.
- (a) Represent function $h(x)=e^{x^3-1}$, as the composition of two functions $f$ and $g$, (b) Provide formulas for the two possible compositions of the two functions: “take the logarithm of” and “take the square root of”.
- Suppose function $f$ performs the operation: “take the logarithm of”, and function $g$ performs: “take the square root of”. (a) Verbally describe the inverses of $f$ and $g$. (b) Find the formulas for these four functions. (c) Find their domains.
- (a) Represent function $h(x)=\sqrt{x^2-1}$ as the composition of two functions $f$ and $g$. (b) Provide a formula for the composition $y=f(g(x))$ of $f(u)=u^{2}+u$ and $g(x)=2x-1$.
- Provide a formula for the composition $y=f(g(x))$ of $f(u)=\sin u$ and $g(x)=\sqrt{x}$.
- Provide a formula for the composition $y=f(g(x))$ of $f(u)=u^{2}-3u+2$ and $g(x)=x$.
- Find the inverse of the function $f(x)= 3x^2+1$. Choose appropriate domains for these two functions.
- (a) Represent the function $h(x)=\sqrt{x-1}$ as the composition of two functions. (b) Represent the function $k(t)=\sqrt{t^2-1}$ as the composition of three functions. (c) Represent the function $p(t)=\sin\sqrt{t^2-1}$ as the composition of four functions.
- (a) What is the composition $f\circ g$ for the functions given by $f(u)=u^2+u$ and $g(x)=3$? (a) What is the composition $f\circ g$ for the functions given by $f(u)=2$ and $g(x)=\sqrt{x}$?
- Is the composition of two functions that are odd/even odd/even?
- Represent this function: $h(x)=\frac{x^3+1}{x^3-1},$ as the composition of two functions of variables $x$ and $y$.
- Represent the composition of these two functions: $f(x)=\frac{1}{x}+1$ and $g(y)=\sqrt{y-1}$, as a single function $h$ of variable $x$. Don't simplify.
- Function $y=f(x)$ is given below by a list its values. Find its inverse and represent it by a similar table. $$\begin{array}{r|l|l|l}x &0 &1 &2 &3 &4 \\\hline y=f(x) &1 &2 &0 &4 &3 \end{array}$$
- What is the function that is its own inverse?
- Plot the inverse of the function shown below, if possible.
- Plot the graph of the inverse of this function:
- Represent this function: $h(x)=\tan (2x)$ as the composition of two functions of variables $x$ and $y$.
- Find the composition $h(x)=(g\circ f)(x)$ of the functions $y=f(x)=x^{2}-1$ and $g(y)=\frac{y-1}{y+1}$. Evaluate $h(0)$.
- Functions $y=f(x)$ and $u=g(y)$ are given below by tables of some of their values. Present the composition $u=h(x)$ of these functions by a similar table:
$$\begin{array}{r|c|c|c|c} x &0 &1 &2 &3 &4 \\ \hline y=f(x) &1 &1 &2 &0 &2 \end{array}$$ $$\begin{array}{c|c|c|c|c} y &0 &1 &2 &3 &4 \\ \hline u=g(y) &3 &1 &2 &1 &0 \end{array}$$
- Find the composition $h(x)=(g\circ f)(x)$ of the functions $y=f(x)=x^{2}-1$ and $g(y)=3y-1.$ Evaluate $h(1)$.
- Represent the composition of these two functions: $f(x)=1/x$ and $g(y)=\frac{y}{y^2-3}$, as a single function $h$ of variable $x$. Don't simplify.
- Represent this function: $h(x)=\frac{x^3+1}{x^3-1},$ as the composition of two functions of variables $x$ and $y$.
- Function $y=f(x)$ is given below by a list of its values. Is the function one-to one? What about its inverse? $$\begin{array}{r|l|l|l|l|l}x&0 &1 &2 &3 &4 \\ \hline y=f(x)&0 &1 &2 &1 &2 \end{array}$$
- Function $y=f(x)$ is given below by a list of its values. Is the function one-to one? What about its inverse? $$\begin{array}{r|l|l|l|l|l}x&0 &1 &2 &3 &4 \\ \hline y=f(x)&7 &5 &3 &4 &6 \end{array}$$
- Function $y=f(x)$ is given below by a list of some of its values. Add missing values in such a way that the function is one-to one. $$\begin{array}{r|l|l|l|l|l}x&-1 &0 &1 &2 &3 &4 &5\\ \hline y=f(x)&-1 & &4 &5 & &2 \end{array}$$
- Plot the graph of the function $f(x)=\frac{1}{x-1}$ and the graph of its inverse. Identify its important features.
- (a) Algebraically, show that the function $f(x)=x^{2}$ is not one-to-one. (b) Graphically, show that the function $g(x)=2^{x+1}$ is one-to-one. (c) Find the inverse of $g$.
- Find the formulas of the inverses of the following functions: (a) $f(x)=(x+1)^3$, (b) $g(x)=\ln (x^3)$.
- Sketch the graph of the inverse of the function below:
Transformations of functions
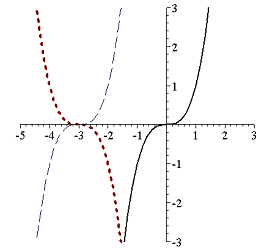
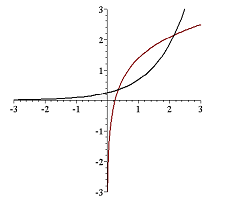
- The graph drawn with a solid line is $y=x^3$. What are the other two?
- The graph of one the functions below is $y=e^x$. What is the other?
- The graphs below are parabolas. One is $y=x^2$. What is the other?
- The graph below is the graph of the function $f(x)=A\sin x+B$ for some $A$ and $B$. Find these numbers.
- The graph of function $f$ is given below. Sketch the graph of $y=2f(x+2)+2$. Explain how you get it.
- By transforming the graph of $y=e^x$, plot the graph of the function $f(x)=2e^{x-3}$. Identify the domain, the range, and the asymptotes.
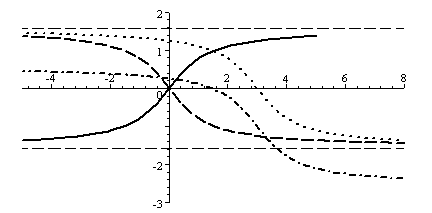
- One of the graphs below is that of $y=\arctan x$. What are the others?
- Half of the graph of an even function is shown below; provide the other half:
- Half of the graph of an odd function is shown below; provide the other half:
- The graph of the function $y=f(x)$ is given below. Sketch the graph of $y=2f(x)$ and then $y=2f(x)-1$.
- What is the relation between these two functions?
- Plot the graph of a function that is both odd and even.
- Give examples of odd and even functions that aren't polynomials.
- Is the inverse of an odd/even function odd/even?
- By transforming the graph of $y=\sin x$, plot the graph of the function $f(x)=2\sin (x-3)$. Identify the domain, the range, and the asymptotes.
- Give examples of an even function, an odd function, and a function that's neither. Provide formulas.
- The graph below is a parabola. Find its formula:
Early models
- The population of a city has doubled in $10$ years. Assuming exponential growth, how long does it take to triple?
- The population of a city has doubled in $10$ years. Assuming exponential growth, how much does it grow every year?
- Provide a formula for modeling radioactive decay. What is the half-life of an element?
- The population of a city declines by $10\%$ every year. How long will it take to drop to $50\%$ of the current population?
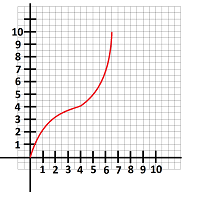
- The function $y=f(x)$ shown below represents the location (in miles) of a hiker as a function of time (in hours). Find the hiker's average velocity.
- A city loses $3\%$ of its population every year. How long will it take to lose $20\%$?
- Find the average rate of change of the function shown below on the interval $[1,6]$:
- A car start moving east from town A at a constant speed of $60$ miles an hour. Town B is located $10$ miles south of A. Represent the distance from town B to the car as a function of time.
Exponentials etc.
- Solve the equation: $2^x=3^{x+1}$. Don't simplify.
- Solve the equation: $3^x=3^{x+1}$.
- Solve the equation: $3^x=2$.
- Solve the equation: $2^x=2\cdot 3^{x+1}$. Don't simplify.
- To what power should you raise $3$ to get $10$?
- Find the domain, the range, and the asymptotes of the function $f(x)=\ln (x-3)+\ln 3$.
Other
- Given vectors $a=<1,2>,\ b=<-2,1>$, find their magnitudes and the angle between them.
- Compute $\displaystyle\sum _{n=1}^{4} n^2$.
- Find the equation of the line starting at the point $(1,2,3)$ in the direction of the vector $<1,1,1>$.
- Set up a system of linear equations -- but do not solve it -- for the following problem: “An investment portfolio worth $\$1,000,000$ is to be formed from the shares of: Microsoft - $\$5$ per share and Apple - $\$7$ per share. If you need to have twice as many shares of Microsoft than Apple, what are the numbers?”
- Set up a system of linear equations -- but do not solve -- for the following problem: “A mix of coffee is to be prepared from: Kenyan coffee - $\$3$ per pound and Colombian coffee - $\$5$ per pound. How much of each do you need to have $10$ pounds of blend with $\$3.50$ per pound?”
- Set up, do not solve, the system of linear equations for the following problem: “One serving of tomato soup contains $100$ Cal and $18$ g of carbohydrates. One slice of whole bread contains $70$ Cal and $13$ g of carbohydrates. How many servings of each should be required to obtain $230$ Cal and $42$ g of carbohydrates?”
- Solve the system of linear equations:
$$\begin{cases} x-y&=2,\\ x+2y&=1. \end{cases}$$
- Solve the system of linear equations and geometrically represent its solution:
$$\begin{cases} x-2y&=1,\\ x+2y&=-1. \end{cases}$$
- Geometrically represent this system of linear equations:
$$\begin{cases} x-2y&=1,\\ x+2y&=-1. \end{cases}$$
- What are the possible outcomes of a system of linear equations?