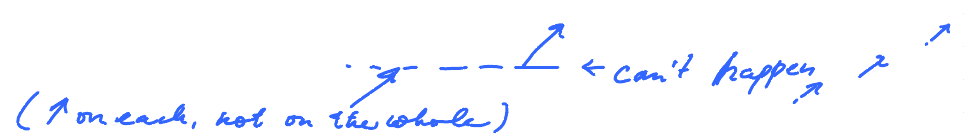Plotting the graph of a function

We can plot the graph of a function simply point by point, a la graphic calculator. Even though this point of view remains the best way to understand what the graph is, the approach is impractical for more complex functions.

These are the issues we're supposed to address:

1. Here we use $f(x)$ only

   * Domain

   * Intercepts

   * Symmetry (Odd and even functions)

   * Periodicity

   * Asymptotes

2. Here we use $f^{\prime}$.

   * Increasing/decreasing

   * Local max/min

   * Global too, possibly

3. Here we use $f^{\prime\prime}(x)$

   * Concavity

   * Inflection points

Let's learn this through examples

Example. Let $$f(x) = \frac{\sin x}{1 + \cos x}.$$ Step by step...

Part 1: using $f$.

Domain:

Recall $\sin$ & $\cos$ are defined for all $x$.

What's left is to make sure there is no division by 0. $$1 + \cos x,$$ solve for $x$. $$\begin{aligned} \cos x &= -1 \\ x&= -\pi + 2k\pi \end{aligned}$$ where $k$ is an integer.

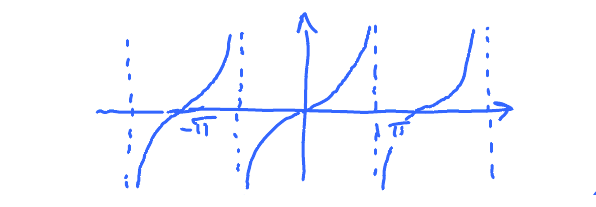
Conclusion about the domain: $$\begin{aligned} D & = \{x: x \neq -\pi + 2k\pi\}, k \text{ integer } \\ & =\ldots \cup (-\pi, \pi) \cup (\pi,3\pi) \cup \ldots \end{aligned} $$ Points are deleted:

Consider now the vertical asymptotes: $$\begin{aligned} \lim_{x \to -\pi} f(x) &= \lim_{x \to -\pi} \frac{\sin x}{1 + \cos x} \quad {\to \over \to} \frac{0}{0} \\ & \overset{\text{LR}}{=} \lim_{x \to -\pi} \frac{\cos x}{-\sin x} \\ &= \lim_{x\to -\pi} -\cot x = \pm \infty \end{aligned}$$ So, $x = -\pi + 2k\pi$ are vertical asymptotes, for each $k$ integer.

What about horizontal asymptotes? Just evaluate the limit $$\lim_{x \to \infty} f(x) = \lim_{x\to\infty}\frac{\sin x}{1+\cos x} \quad \left.{ \gets \text{ periodic} \over \gets \text{ periodic}} \right| \text{d.n.e} $$ So, no horizontal asymptotes.

Next...

$x$-intercepts

To find solve $f(x) = 0$, $$\begin{aligned} \frac{\sin x}{1 + \cos x} &= 0, \quad \sin x = 0 \\ x &= k\pi, \end{aligned}$$ where $k$ is an integer.

$y$-intercept

Set $x=0$, then $$ f(0) = \frac{\sin 0}{a + \cos 0} = 0.$$

Symmetry

Plug in $-x$ and see if we can get $f$. $$\begin{aligned} f(-x) &= \frac{\sin (-x)}{1 + \cos(-x)} \\ & = \frac{-\sin x}{1+ \cos x} \\ & = -\frac{\sin x}{1 + \cos x} \\ & = -f(x) \end{aligned}$$ So $f$ is odd.

Periodicity

$\sin$, $\cos$ are periodic with period $2\pi$: $$\begin{aligned} \sin (x + 2 \pi) &= \sin x \\ \cos (x + 2 \pi) &= \cos x \end{aligned}$$

Substitute

$$\begin{aligned} f(x + 2\pi) &= \frac{\sin(x + 2\pi)}{1 + \cos (x + 2pi)} \\ &= \frac{\sin x}{1 + \cos x} \\ &= f(x) \end{aligned}$$ So $f$ is $2\pi$-periodic.

Part 2: using $f^\prime$.

$$\begin{aligned} f^{\prime}(x) &= \left(\frac{\sin x}{1 + \cos x}\right)^{\prime} \\ & \overset{\text{QR}}{=} \frac{\cos x (1 + \cos x) - (-\sin x)\sin x}{(1 + \cos x)^{2}} \\ &= \frac{\cos x + \cos^{2}x + \sin^{2}x}{(1 + \cos x)^{2}} \\ \text{PT} &= \frac{\cos x + 1}{(1 + \cos x)^{2}} \\ &= \frac{1}{1 + \cos x} \end{aligned}$$ Now solve for $x$: $$\frac{1}{1+\cos x} = 0.$$ Never holds! Hence, no such $x$.

What is the sign of $\frac{1}{1+\cos x}$ then? It's positive $\frac{1}{1+\cos x} >0$ since $\cos x \geq 1$ always $$ 1 + \cos x \geq 0$$

So $$f^{\prime}(x) > 0,$$ if $x$ is in the domain of $f$.

Wrong: So, $f$ increasing, on domain of $f$: $$\ldots, (-\pi,\pi) \cup (\pi,3\pi) \cup \ldots$$ Conclusion that positive derivative means increasing behavior holds only for intervals!

Right: $f$ increases on each of the intervals: $$(-\pi,\pi), (\pi,3\pi), \text{etc}$$ On each but not on the whole...

In fact, it's periodic. So it can't be increasing throughout.

Part 3: using $f^{\prime\prime}$

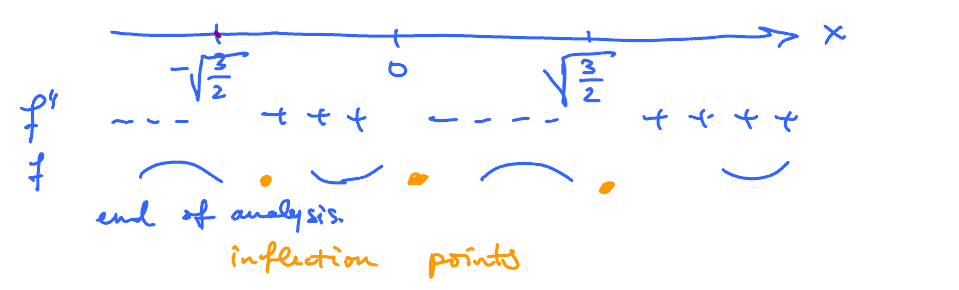
Compute the second derivative. $$\begin{aligned} \lim_{x \to \pm \infty} xe^{-x^{2}} &= \lim_{x \to \pm\infty} \frac{x}{e^{x^{2}}} \\ &\overset{\text{LR}}{=} \lim_{x \to \pm\infty} \frac{(x)^{\prime}}{(e^{x^{2}})^{\prime}} \\ &= \lim_{x \to \pm\infty} \frac{1}{\underbrace{2x}_{\pm\infty}e^{x^{2}}} = 0 \end{aligned}$$ Next, set $f^{\prime\prime}(x) = 0$, and solve for $x$ $$\sin x = 0,$$ so $x = \pi + 2k\pi$, where $k$ is an integer.

$$\begin{aligned} f^{\prime\prime}(x) & > 0 \text{ on } (-\pi,0) \text{ concave up} \\ f^{\prime\prime}(x) & < 0 \text{ on } (0,\pi) \text{ concave down} \end{aligned}$$

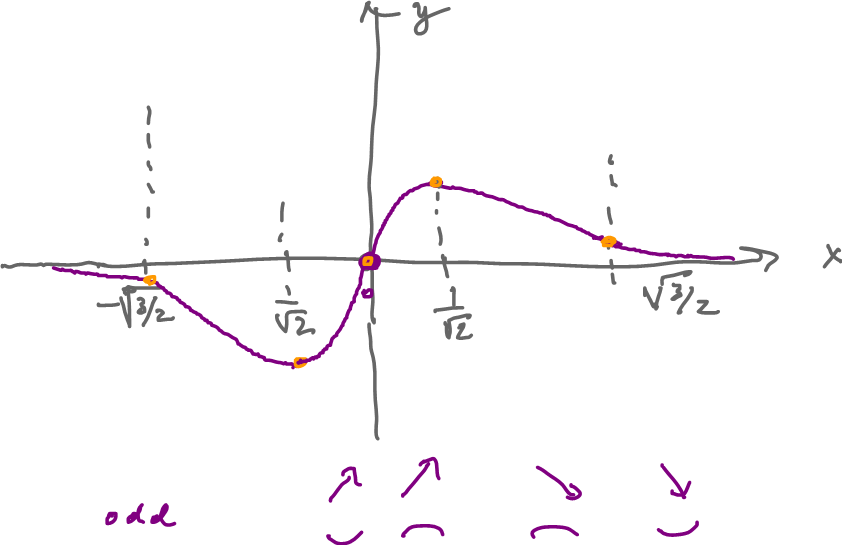
End Result

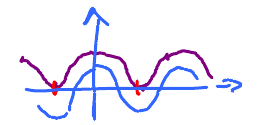
Keep in mind that the graph is only a way to verify the answer. The sketch is much less important than the data we have found.

Example. Let $$f(x) = xe^{-x^{2}}.$$

Part 1: using $f$

Domain 

$(-\infty,\infty)$ because $x$ & $x^{2}$, $e^{x}$ are defined for all $x$.

Vertical asymptotes 

none, because of the same reason and there is no division.

Horizontal Asymptotes 

Compute $\lim\limits_{x \to \pm\infty} f(x)$

Note: when $f$ is rational, then $\lim_{x \to \infty} f(x)$ (one limit) is sufficient. If not, you need $\lim_{x\to \pm\infty} f(x)$, i.e. two limits. $$\begin{aligned} \lim_{x \to \pm \infty} xe^{-x^{2}} &= \lim_{x \to \pm\infty} \frac{x}{e^{x^{2}}} \\ &\overset{\text{LR}}{=} \lim_{x \to \pm\infty} \frac{(x)^{\prime}}{(e^{x^{2}})^{\prime}} \\ &= \lim_{x \to \pm\infty} \frac{1}{\underbrace{2x}_{\pm\infty}e^{x^{2}}} = 0 \end{aligned}$$

$y=0$ is a horizontal asymptote at $\pm\infty$ and $-\infty$.

$x$-intercepts 

$xe^{-x^{2}} = 0$, solve for $x$.

$x=0$ works, if $x \neq 0$, then $e^{-x^{2}} = 0$ but $e^{x} \neq 0$, no none here. So $x=0$ is the only $x$-intercept. Same as the $y$-intercept.

Periodicity 

None

Symmetry 

$$\begin{aligned} f(-x) &= (-x) e^{-(-x)^{2}} \\ &= -x e^{-x^{2}} \\ &= -f(x)\end{aligned}$$

So $f$ is odd.

Part 2: using $f^{\prime}$

$$\begin{aligned} f^{\prime} &= \left( x e^{-x^{2}}\right)^{\prime}\\ &= e^{-x^{2}} + x\left( e^{-x^{2}} \right)^{\prime} \\ & = e^{-x^{2}} - 2x^{2}e^{-x^{2}} \\ & = e^{-x^{2}} \underbrace{( 1 - 2x^{2})}_{\text{only look at this}} \end{aligned}$$

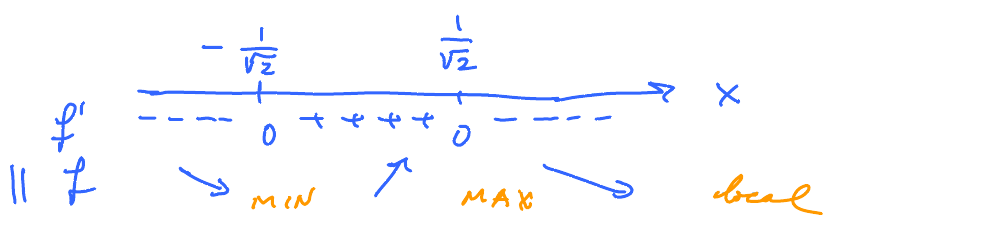
Is $f^{\prime}(x) > 0$ or $f^{\prime}(x) < 0$? We look at and solve $f^{\prime}(x) = 0$.

$$\begin{aligned} ( 1 - 2x^{2}) &= 0 \\ 2x^{2} &= 1 \\ x^{2} &= \frac{1}{2} \\ \therefore x &= \pm \frac{1}{\sqrt{2}} \end{aligned}$$

These are the only critical points.

Part 3: using $f^{\prime\prime}$

$$\begin{aligned} f^{\prime\prime}(x) &= \left( e^{-x^{2}} ( 1 - 2 x^{2} ) \right)^{\prime} \\ &= -2xe^{-x^{2}} ( 1 - 2x^{2}) + e^{-x^{2}} (-4x) \\ &= e^{-x^{2}} \underbrace{( -2x + 4x^{3} - 4x)}_{\text{Cubic Polynomial}} \\ & = \underbrace{e^{-x^{2}}}_{\to 0} \underbrace{2x(2x^{2} - 3)}_{\text{look at this only}} = 0 \end{aligned}$$ Solving, we get $$ x=0, \qquad x = \pm\sqrt{\frac{3}{2}} $$

Optimization = Finding max/min globally.