Internal structure of a vector space: part 2

Vector spaces as spans

Example: Suppose $u,v$ aren't multiples of each other. Then these are planes:

• ${\rm span}\{u,v,v\}$,
• ${\rm span}\{u,v,0\}$,
• ${\rm span}\{u,v,\lambda v\}$,
• ${\rm span}\{u,v,u+v\}$.

More generally: ${\rm span}\{u,v,au+bv\} = {\rm span}\{u,v\} = {\rm plane}$.

Observation: In these examples, adding a third vector doesn't enlarge the span!

This is called linear dependence.

Homework: Prove that no finite set of polynomials spans ${\rm P}$, the vector space of all polynomials: $${\rm span \hspace{3pt}} S \neq {\rm P}.$$

Example: To find the span of $$v_1=(1,0,0), v_2=(1,2,1), v_3=(1,3,1) \in {\bf R}^3,$$ we need to find all possible $(a,b,c)$ such that $$x(1,0,0)+y(1,2,1)+z(1,3,1) = (a,b,c)$$ for some $x,y,z$.

Rewrite: $x \left[ \begin{array}{} 1 \\ 0 \\ 0 \end{array} \right] + y\left[ \begin{array}{} 1 \\ 2 \\ 1 \end{array} \right] + z \left[ \begin{array}{} 1 \\ 3 \\ 1 \end{array} \right] = \left[ \begin{array}{} a \\ b \\ c \end{array} \right]$.

Now we need to find $x,y,z$ for the given $a,b,c$.

After some vector algebra, we get this:

$\left[ \begin{array}{} x+y+z \\ 0 + 2y + 3z \\ 0 + y + z \end{array} \right] = \left[ \begin{array}{} a \\ b \\ c \end{array} \right]$

Both sides are vectors in ${\bf R}^3$.

Break up component-wise:

$\left\{ \begin{array}{} x&+y &+z &= a \\ & 2y &+3z &= b \\ & y &+ z &= c \end{array} \right.$

Same procedure as if $a,b,c$ are specific.

One step ($E_2-2E_3$):

$\left\{ \begin{array}{} z &+ y &+ z &= a \\ & 2y &+ 3z &= b \\ & & z &= b - 2c \end{array} \right.$ ($*$).

Now just do the back substitution and you can find $x,y,z$.

So, the answer to "Can $(a,b,c)$ be represented this way?" is Yes.

Hence $(a,b,c) \in {\rm span}\{v_1,v_2,v_3\}$.

Since $(a,b,c)$ was arbitrary, then ${\rm span}\{v_1,v_2,v_3\} = {\bf R}^3$.

Question: When could the answer be No?

Imagine: $E_3$ is $0=b-2c$, then what? The answer is still yes, if $0=b-2c$. So not every $(a,b,c)$ is in the span! (Example (1,1,1))

Imagine: $E_3$ is $0=0$, then what?

Note: In all of the above examples, span has been a subspace.

Theorem: Given a non-empty finite set $\{v_1,\ldots,v_n\}$ in a vector space $V$, its span is a subspace of $V$.

Proof: Use the subspace theorem again. Three conditions...

Let $T = {\rm span}\{v_1,\ldots,v_n \}$.

Condition 1. Observe $v_1,\ldots,v_n \in T$, so $T \neq \emptyset$.

Condition 2. Given $u,w \in T$, show that $u+w \in T$.

They are linear combinations of $v_1,\ldots,v_n$:

• $u = a_1v-1+\ldots+a_nv_n,$ for some $a_1,\ldots,a_n \in {\bf R}$ and
• $w=b_1v_1+\ldots+b_nv_n$.

Then

• $u+w=(a_1+b_1)v_1+\ldots+(a_n+b_n)v_n$.

This is a linear combination of $v_1,\ldots,v_n$, so $u+w \in T$. We conclude that it's "closed under addition."

Condition 3. Given $u \in T$, $r \in {\bf R}$, some $a_1,\ldots,a_n \in {\bf R}$.

Again:

• $ru = r(a_1v_1+\ldots+a_nv_n) = (ra_1)v_1+\ldots+(ra_n)v_n$,

which is a linear combination of $v_1,\ldots,v_n$, so $rn \in T$.

So, it's "closed under scalar multiplication." $\blacksquare$

We can define ${\rm span \hspace{3pt}} S$, even if $S$ is infinite: $${\rm span \hspace{3pt}} S = \{a_1v_1 + \ldots + a_nv_n \colon v_1 \ldots v_n \in S, a_1 \ldots a_n \in {\bf R} \}$$ the set of all linear combinations of the elements of $S$.

Example: Is ${\rm span \hspace{3pt}} S$ still a subspace when $S$ is infinite?

Redundancy in spans, linear independence

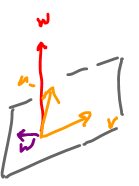
Recall this situation. Suppose $S = {\rm span}\{u,v\}={\bf R}^2$, then $T={\rm span}\{u,v,au+bv\}=S$. So, a new vector doesn't contribute to the span.

It's easy to see geometrically.

In ${\bf R}^3$, ${\rm span}\{u,v\}$ looks like this (black plane):

.

What if we add $w=au+bv$ with $a,b$ fixed?

Clearly, if $w$ is chosen within ${\rm span}\{u,v\}$ (purple), it's redundant!

How do we explain this algebraically?

Compare:

• $S$ consists of $pu+rv$, $p,r \in {\bf R}$ and
• $T$ consists of $xu+yv+z(au+bv)=(x+za)u+(y+zb)v$, $x,y,z \in {\bf R}$,

which is once again a linear combination of $u$ and $v$.

Then this element belongs to $S$. So $T \subset S$.

On the other hand, $S \subset T$ because I can represent $pu+rv$ as $xu+yv+z(au+bv)$, by letting $x=p$, $y=r$, $z=0$.

So, $T=S$.

Thus the presence in the set of linear combinations of the other elements is redundant, as far as the span is concerned.

Therefore elements can be removed when they are dependent on the others -- without changing the span.

The definition is the contrapositive to this idea.

Definition: Given a finite set $\{v_1,\ldots,v_n\}$ in $V$, it is called linearly independent if $a_1v_1+\ldots+a_nv_n=0$ implies that $a_1=a_2=\ldots=a_n=0$. Otherwise, the set is linearly dependent.

Example: For $u=5v$, $S=\{u,v\}$ is linearly dependent because there is a non-trivial linear combination of $u, v$ that adds up to $0$.

Find what to plug in: $-\frac{1}{5}u+1v=0$, $-\frac{1}{5} \neq 0$, $1 \neq 0$.

Theorem: $\{u,v\} \subset V$ is linearly dependent if and only if $v$ is a multiple of $u$ or vice versa.

Proof: ($\Rightarrow$) If $\{u,v\}$ is linearly dependent, then take the negation of the definition:

• for any $a,b \in {\bf R}$, $au+bv=0$ implies $a=b=0$.

This is the negation:

• for some $a, b \in {\bf R}$, $au+bv=0$, but $a \neq 0$ or $b \neq 0$.

This is given, prove $u=\lambda v$ for some $\lambda$, i.e., we have $a,b$, find $\lambda$.

Let $\lambda = -\frac{b}{a}$, then $au+bv=0$ implies $u=-\frac{b}{a}v$, done...

Comments?

What if $a=0$? Problem...

Let's fix the proof (use $a,b\neq0$).

• Case 1: Suppose $a\neq0$. Then let $\lambda = -\frac{b}{a}$, then $au+bv=0$ implies $u=-\frac{b}{a}v$.

• Case 2: Suppose $b \neq 0$. Find $\mu$ such that $v=\mu u$. Let $\mu = -\frac{a}{b}$, then $au+bv$ implies $v = -\frac{a}{b}u$.

($\Leftarrow$) Assume $v=\lambda u$. Need to show the negation of the definition holds.

Note: Original: $A \Rightarrow B$. Contrapositive: $B \Rightarrow A$. Negative: $\neg B \Rightarrow \neg A$.

We have $\lambda$, find $a,b$.

Let $a = ?$, $b = ?$.

How about: $v = \lambda u$ or $\lambda u - v = 0$?

So choose $a = \lambda$, $b=-1$. (no division by $0$!)

Next, assume $u=\mu v$, then same proof. $\blacksquare$

This was for two vectors. Let's generalize the theorem to the case of many vectors.

How?

"$v_1, \ldots, v_n \subset V$ is linearly dependent if and only if..."

What's the analogue of "is a multiple of the other"?

Answer: "is a linear combination of the rest".

Theorem: $v_1, \ldots, v_n \subset V$ is linearly dependent if and only if one of the vectors is a linear combination of the rest.

Proof: We follow the same idea...

($\Leftarrow$) The order of vectors doesn't matter, let's assume it's last one:

• (1) $v_n = \lambda_1v_1 + \ldots+\lambda_{n-1}v_{n-1}$.

Need to show the negation of the definition. Find $a_1,\ldots,a_n$ such that

• (2) $a_1v_1+\ldots+a_{n-1}v_{n-1}+a_nv_n=0$.

and not all $a_1,\ldots,a_n$ is $0$.

Compare these (1),(2).

Let's re-write (1):

• (3) $\lambda_1v_1 + \ldots+\lambda_{n-1}v_{n-1} - v_n=0$

This way they are aligned!

Need (3) $\rightarrow$ (2). Choose

• $a_1=\lambda_1,\ldots,a_{n-1}=\lambda_{n+1}a_n=-1$.

Done, since the coefficients are the same and $a_n \neq 0$.

Sidenote: What if $n=1$? What is linear independence of $\{v_1\}$? Use the definition: $a_1v_1=0$ implies $a_1=0$. So?

• $\{v \neq 0\}$ always linearly independent,
• $\{v=0\}$ always linearly dependent.

Exercise: What does adding $0$ to a set do to its linear independence?

Back to the proof.

($\Rightarrow$) Given that $\{v_1,\ldots,v_n\}$ is linearly dependent, prove one of them is a linear combination of the rest.

Rewrite:

• (4) $a_1v_1+\ldots+a_nv_n=0$ with not all $a_1,\ldots,a_n=0$.

The order doesn't matter, assume $a_n \neq 0$. Show $v_n$ is a linear combination of $v_1, \ldots, v_{n-1}$.

Since $a_n \neq 0$, we rewrite (4) as

• $\frac{a_1}{a_n}v_1 + \ldots + \frac{a_{n-1}}{a_n}v_{n-1}+v_n=0$, so
• $v_n = -\frac{a_1}{a_n}v_1 - \ldots - \frac{a_{n-1}}{a_n}v_{n-1}$.

$\blacksquare$

The idea of the proof is simple: pull one of the vectors from the left hand side to the right hand side or vice versa.

More on vector spaces as spans

Given a subset $S$ of a vector space $V$, we say that $S$ spans $V$ if ${\rm span \hspace{3pt}} S=V$.

So $$V= \{ a_1v_1+\ldots+_nv_n \colon a_1, \ldots, a_n \in {\bf R}, v_1 \ldots v_n \in S \}.$$

To determine that, we solve a system of linear equations.

Given a subset $S$ of a vector space $V$, we say that $S$ is linearly independent if for every $v_1,\ldots,v_n \in S$, $a_1v_1 + \ldots + a_nv_n =0$ implies $a_1=\ldots=a_n=0$.

To determine that, we solve a system of linear equations.

Example: Let $V={\bf R}^3$. Consider these spans below. The vectors are:

linearly independent: $\left\{ \begin{array}{} {\rm span}\{(1,0,0),(0,1,0),(0,0,1)\} &= {\bf R}^3 \\ {\rm span}\{(1,0,0),(1,1,0),(1,1,1)\} &= {\bf R}^3 \\ \end{array}{} \right\}$

linearly dependent: $\left\{ \begin{array}{} {\rm span}\{(1,0,0),(1,1,0),(1,1,1),(5,5,5)\} &= {\bf R}^3 \\ {\rm span \hspace{3pt}} {\bf R}^3 &= {\bf R}^3 \\ {\rm span}\{x-{\rm axis \hspace{3pt}} \cup y-{\rm axis \hspace{3pt}} \cup z-{\rm axis}\} &= {\bf R}^3 \end{array}{} \right\}$

So, very different sets span the same vector space.

Some are clearly too large. Some are "small".

We interested in the smallest ones, i.e., the ones without redundancy.

They are called bases of the space. However, we'll approach this issue from a different direction.

Observe:

• Fact 1: If $S$ spans $V$ then $S \cup A$ also spans $V$, for any set $A$.
• Fact 2: If $S$ is linearly dependent, $S \cup A$ is also linearly dependent.

The concept of basis of vector space

Definition: If a subset $S$ of $V$ is both linearly independent and spans $V$, then $S$ is called a basis of $V$.

Example: $i=(1,0,0)$, $j=(0,1,0)$, $k=(0,1,1)$ is the standard basis of ${\bf R}^3$.

Example: But this is also a basis: $(1,0,0)$, $(1,1,0)$, $(1,1,1)$.

Question: Is basis well defined?

To clarify the issue let's go back to calculus...

Recall the definition: The limit $\displaystyle\lim_{x \rightarrow a} f(x)$, is a number $L$ satisfying a certain condition ($\epsilon$-$\delta$).

Question: What can go wrong here?

Answer: What if it doesn't exist?

• 1. $\displaystyle\lim_{x \rightarrow 0}\left( \frac{1}{x}\right)-\lim_{x \rightarrow 0}\left( \frac{1}{x} \right) = 0$ becomes $L-L=0$, which is algebra with non-existing entities!
• 2. $\stackrel{\rm Thm?}{=} \displaystyle\lim_{x \rightarrow 0} \left( \frac{1}{x} - \frac{1}{x} \right) = \lim_{x \rightarrow 0} 0 = 0$, but the limits don't exist!

The problem is that the definition is "indirect". There is no algorithm for finding it, unlike, for example, addition.

Compare:

• Limit = number with certain condition.
• Basis = set with certain condition.

Does it exist? The answer isn't obvious.

We prove the answer is yes for ${\bf R}^n$.

Take $$\gamma = \{(1,0,\ldots,0), (0,1,0,\ldots,0), \ldots, (0,\ldots,0,1)\},$$ the standard basis of ${\bf R}^n$ commonly denoted by $$ = \{e_1,e_2,\ldots,e_n\}.$$

Theorem: The standard basis $\gamma$ is a basis of ${\bf R}^n$.

Proof:

• 1. ${\rm span \hspace{3pt}} \gamma = {\bf R}^n$.

For any vector $v=(a_1,\ldots,a_n)$, it is a linear combination of elements of $\gamma$

Indeed: $v=(a_1,\ldots,a_n)=a_1e_1 + a_2e_2 + \ldots + a_ne_n.$

• 2. $\gamma$ is linearly independent.

Suppose $a_1e_1 + \ldots + a_ne_n = 0$, rewrite:

$a_1 \left[ \begin{array}{} 1 \\ 0 \\ \vdots \\ 0 \end{array} \right] + \ldots + a_n \left[ \begin{array}{} 0 \\ \vdots \\ 0 \\ 1 \end{array} \right ] = 0$,

Or:

$\left[ \begin{array}{} a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right ] = \left[ \begin{array}{} 0 \\ 0 \\ \vdots \\ 0 \end{array} \right ]$

So $a_1=0$, $a_2=0$, $\ldots$, $a_n=0$. $\blacksquare$

We will prove that any subspaces of ${\bf R}^n$ have a basis.

Example: The polynomials ${\bf P}$.

Homework was: No finite subset $S$ of ${\bf P}$ spans ${\bf P}$. So, a basis of ${\bf P}$ has to be infinite.

Specifically, consider $$\gamma = \{1, x , x^2, \ldots, x^2, \ldots\}.$$

Exercise: Prove this is a basis.

Another basis will be as large, example: $$\gamma = \{1, (x-1), (x-1)^2, \ldots, (x-1)^n, \ldots\}.$$

More details. "Sorry for the long letter; I didn't have time to write a short one."

Let

• $S$ be the set, $S = \{p_1, \ldots, p_k\}$,

then let

• $n={\rm max}\{{\rm deg \hspace{3pt}} p_i \colon i=1,\ldots,k \}$,

and let

• $q=x^{n+1}$.

Prove that $q \not \in {\rm span \hspace{3pt}} S$.

Use this:

• ${\rm span \hspace{3pt}} S=\{{\rm span \hspace{3pt}}S' \colon S' \subset S, S'$ is finite$\}$ $= \{a_1v_1+\ldots+a_nv_n \colon v_1, \ldots, v_n \in S$, $a_1, \ldots, a_n \in {\bf R} \}$.
• $S$ is linearly independent if every $S' \subset S$ is linearly independent.

Homework:

• Hint 1. Use fact: if two polynomials are equal, then their corresponding coefficients are equal.
• Hint 2. No infinite sums!

How large is the vector space?

Definition: A vector space is called finite-dimensional if it has a finite basis, otherwise infinite-dimensional.

Example:

• ${\bf R}^n$ is finite dimensional while
• ${\bf P}$ is infinite dimensional.

All finite dimensional spaces are "like" ${\bf R}^n$. As a result bases can be found, easily.

Not so easy for infinite dimensional spaces.

Example: What is a basis of $C({\bf R})$, ${\bf F}({\bf R})$ (functions)?

Example: Take $V={0}$. What is its basis?

How about $\gamma = \{0\}$?

• 1. ${\rm span \hspace{3pt}} \gamma = \{ 0\}$
• 2. Is it linearly independent? No.

So, $\gamma = \emptyset$.

Definition: Given a vector space $V$, its dimension is the number of elements in its basis.

In particular, ${\rm dim}\{0\}=0$.

Question: Is it well defined?

Homework: Prove that the set of all powers form a basis of the space of all polynomials.

Question: What can go wrong?

Let's rewrite: The dimension of $V$ is the number of elements in a basis of $V$.

This already suggest some issues to deal with.

Question 1: Is there a basis? (Note: not $\{0\}$)

Assume that there is.

Question 2: What if there are infinitely many elements?

Question 3: Mismatched "the" vs. "a". There may be bases with different number of elements.

Compare to the concept of "the" limit. Rrcall the definition: a/the number satisfying a certain property. But we aren't allowed to use "the" until proven that there is only one. usually, prove the uniqueness by assuming there is two, not equal, finding contradiction.

(start with $\epsilon = \frac{(M-L)}{2}$, then show that there is no $\delta$.)

This isn't what we should expect:

• $V \rightarrow$ basis $\rightarrow$ dimension

This is:

We need to show that all bases have the same number of elements.

Lesson: In definitions, consider

• 1. existence,
• 2. uniqueness.

This will ensure that the concept is well defined.

Bases and dimensions

We develop some theory to deal with these issues. This is what we are after.

Comparison Theorem: Suppose

• 1. $V = {\rm span}\{w_1,\ldots,w_n\}$,
• 2. $\{v_1,\ldots,v_m\}$ is linearly independent.

Then $n \geq m$.

Let's start with the case of $n=1$.

Instance:

• 1. $V = {\rm span}\{w_1\}$ (a line).
• 2. $\{v_1,\ldots,v_m\}$ is linearly independent.

Then $m=1$.

Proof: So, we need to show that every linearly independent set has one element. It's geometrically obvious but we want to do it algebraically so that we can apply the ideas to the general case.

$V = {\rm span}\{w_1\}$, so every element $v \in V$ is a linear combinations of $w_1$, i.e., it's a multiple of $v$.

Apply this to each $v_1,\ldots,v_m$:

(*) $\left\{ \begin{array}{} v_1 = a_1w_1 \\ \vdots \\ v_m = a_mw_1 \end{array} \right.$

for some $a_1,\ldots,a_n \in {\bf R}$.

Proof of contradiction, assume $m>1$.

Contradiction with what? Condition 2, we'll show that $v_1,\ldots,v_m$ are linearly dependent, i.e., there are $c_1,\ldots,c_m \in {\bf R}$ not all $0$ such that $$c_1v_1+\ldots+c_mv_m=0.$$

Where do they come from? From (*).

Consider just two: $v_1 = a_1w_1$ and $v_2=a-2w_1$.

What linear combination of $v_1,v_2$ gives us $0$?

(**) $\left\{ \begin{array}{} \frac{1}{a_1}v_1 = w_1 \\ \frac{1}{a_2}v_2 = w_1 \end{array} \right.$, so $\frac{1}{a_1}v_1-\frac{1}{a_2}v_2=0$.

As long as $a_1,a_2 \neq 0$. If $a_1=0$, then $v_1=0$, then $\{v_1,\ldots,v_m\}$ is linearly dependent. $\blacksquare$

Lesson: $c_1=\frac{1}{a_1}$, $c_1 = -\frac{1}{a_2}$, they are solutions to a system. ($a_1x_1+a_2x_2=0$)