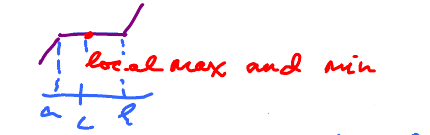Fermat's Theorem

Suppose $c$ is a local extreme point of $y = f(x)$. Then $$\left.\begin{aligned} f^{\prime}(c) & = 0 \quad \text{ or } \\ f^{\prime}(c) & \text{ does not exist} \end{aligned} \right\} \qquad \text{called critical points}. $$

Plan: To find max/min (global), find all critical points. What about vice versa? "Converse": local

$f^{\prime}(c) = 0$ then $c$ is a local extreme point of $f$. Not true!

Example

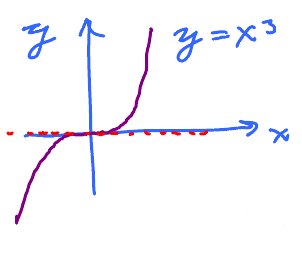
$f(x) = x^{3}$ at $x = 0$

$$\begin{aligned} f^{\prime}(x) &= 3x^{2} \\ f^{\prime}(0) & = 0 \end{aligned}$$ but this is not an extreme point.

Example

$$f(c) \begin{cases} & = f(x) \qquad \text{ on } (a, b) \\ & \leq \qquad \text{hold} \\ & \geq \qquad \text{hold} \end{cases}$$

Example: Global Extreme Points

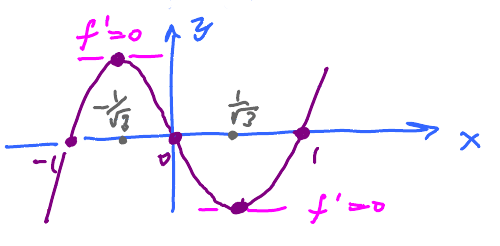
Find global extreme points of $y = f(x) = x^{3} - x$ on $[-2, 5]$.

Step 1:

Find all critical points. How? Use Fermat's theorem: $$ f^{\prime}(x) = 3x^{2} - 1 $$ Set it to 0, and solve for $x$. $$\begin{aligned} 3x^{2} - 1 &= 0 \\ x^{2} &= \frac{1}{3} \\ x & = \pm \frac{1}{\sqrt{3}} \end{aligned}$$ There are 2 critical points.

Step 2:

Compare the values of $f$ at these points and the end points of the interval $$\left.\begin{aligned} x: y &= x^{3} - x = x(x^{2} - 1) \\ \frac{1}{\sqrt{3}}: &\frac{1}{\sqrt{3}}\left(\frac{1}{3} - 1 \right) = -\frac{2}{3\sqrt{3}} \\ -\frac{1}{\sqrt{3}}: &-\frac{1}{\sqrt{3}}\left(-\frac{1}{3} - 1 \right) = \frac{2}{3\sqrt{3}} \\ -2&: -8 + 2 = -5 \gets \text{ min } \\ 5&: 12.5 - 5 = 120 \gets \text{ max } \end{aligned} \right\} \qquad \text{global}$$ $$\left.\begin{aligned} -2 &: -8 + 2 = -5 \gets \text{ min } \\ 5 &: 12.5 - 5 = 120 \gets \text{ max } \end{aligned} \right\} \qquad \text{global}$$

$$\lim_{x \to \pm\infty}(x^{3} - x) = \pm\infty$$

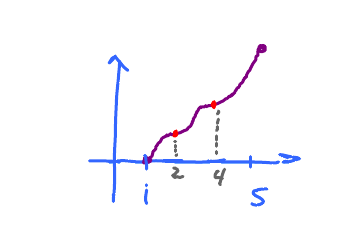
Example: No Local Max/Min

Plot with no local max/min showing critical points at 2, 4. Graph is continuous on $[1,5]$.

Exercise

$$f(x) = 2x^{3} - 3x^{2} - 12x + 1 $$ on $[-2,3]$. $$f^{\prime}(x) = 6x^{2} - 6x - 12 $$ defined for all $x$. Solve $$\begin{aligned} 6x^{2} - 6x - 12 &= 0 \\ x^{2} -x - 2 &= 0 \\ \text{QF} \qquad x &= \frac{1 \pm \sqrt{1 - (-2)4}}{2} \\ &= \frac{1 \pm 3}{2} = 2,1 \end{aligned}$$

$ $	$x$	$y$
Critical Points	2	$2\cdot 2^{3} - 3 \cdot 2^{2} - 12 \cdot 2 + 1 = 16 - 12 - 24 + 1 = -19$
Critical Points	-1	$2\cdot (-1)^{3} - 3 \cdot (-1)^{2} - 12 \cdot (-1) + 1 = -2 - 3 +12 + 1 = 8$
End Points	-2	$2\cdot (-2)^{3} - 3 \cdot (-2)^{2} - 12 \cdot (-2) + 1 = -16 - 12 + 24 + 1 = -3$
End Points	3	$2\cdot 3^{3} - 3 \cdot 3^{2} - 12 \cdot 3 + 1 = 54 - 27 -36 + 1 = -8$

Answer

• Global max value is $y = 8$ attained at $x = -1$ ( global max points).
• Global min value is $y = 19$ attained at $x = 2$ ( global min points).
• Global max is (-1,8), point on the graph.