This site is being phased out.
College Algebra -- Fall 2014 -- final exam
Name:_________________________ $\qquad$ 12 problems, 10 points each
- Justify every step you make with as thorough an explanation as possible, in English.
- Unless requested, no decimal representation of the answers is necessary.
- Start every problem at the top of the page.
$\bullet$ 1. Solve the following equation: $\left( x^2-7 \right)^3 -8=0$.
$\bullet$ 2. What is the distance from the center of the circle $(x-1)^2+(y+3)^2=5$ to the origin?
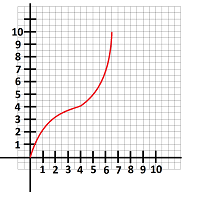
$\bullet$ 3. Plot the graph of the function $y=f(x)$, where $x$ is the income (in thousands of dollars) and $f(x)$ is the tax bill (in thousands of dollars) for the income of $x$, which is computed as follows: no tax on the first $\$ 10,000$, 5% for the next $\$ 10,000$, 10% for the rest of the income.
$\bullet$ 4. For the polynomial $f(x)=-2x(x-2)^2(x+1)^3$, find its $x$-intercepts and its large scale behavior, i.e., $f(x)\to ?$ as $x\to \pm \infty$.
$\bullet$ 5. Represent the composition of these two functions: $f(x)=1/x$ and $g(y)=\frac{y}{y^2-3}$, as a single function $h$ of variable $x$. Don't simplify.
$\bullet$ 6. Represent this function: $h(x)=\frac{x^3+1}{x^3-1},$ as the composition of two functions of variables $x$ and $y$.
$\bullet$ 7. Functions $y=f(x)$ and $u=g(y)$ are given below by tables of some of their values. Present the composition $u=h(x)$ of these functions by a similar table: $$\begin{array}{c|c|c|c|c} x &0 &1 &2 &3 &4 \\ \hline y=f(x) &1 &1 &2 &0 &2 \end{array}$$ $$\begin{array}{c|c|c|c|c} y &0 &1 &2 &3 &4 \\ \hline u=g(y) &3 &1 &2 &1 &0 \end{array}$$
$\bullet$ 8. Plot the graph of the inverse of this function:
$\bullet$ 9. Solve the equation: $2^x=3^{x+1}$. Don't simplify.
$\bullet$ 10. By transforming the graph of $y=e^x$, plot the graph of the function $f(x)=2e^{x-3}$. Identify the domain, the range, and the asymptotes.
$\bullet$ 11. Your savings account pays 3% per year (compounded interest). How long will it take to double your money?
$\bullet$ 12. Set up a system of linear equations -- but do not solve it -- for the following problem: "An investment portfolio worth $\$1,000,000$ is to be formed from the shares of: Microsoft - $\$5$ per share and Apple - $\$7$ per share. If you need to have twice as many shares of Microsoft than Apple, what are the numbers?"