This site is being phased out.
Calculus I -- Fall 2012 -- final exam
Name:_________________________
- Show enough work to justify your answers
- Write the problems in the given order, each problem on a separate page.
- Don't simplify unless very easy or absolutely necessary.
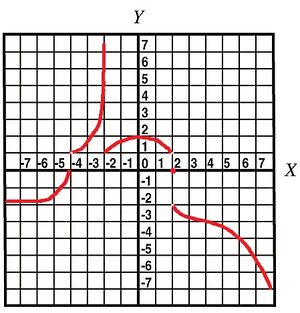
1. A sketch of the graph of a function $f$ is given below. Provide the important limits of $f$ that describe its behavior.
2. Differentiate $$\frac{\ln(\sin x)}{x}.$$
3. (a) State the definition of the derivative of function $f$ at point $x=a$ as a limit. (b) Sketch an illustration of this definition for $f(x)=x^2$ and $a=1$.
4. Find the linear approximation of $f(x)=\ln (x)$ at $a=1$. Use it to estimate $\ln(.99)$.
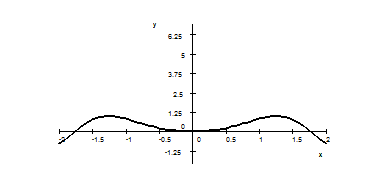
5. The graph of function $f$ is given below. Sketch the graph of the antiderivative $F$ of $f$ that satisfies $F(0)=1$.
6. Sketch the graph of the function $f(x)=x^{4}-x^2$. Provide justification for each feature of the graph.
7. Find the point on the parabola $y^2=2x$ that is closest to the point $(1,4)$.
8. A ladder 10 ft long rests against a vertical wall. If the bottom of the ladder slides away from the wall at the rate 1 ft/sec, how fast is the top of the ladder sliding down the wall when the bottom of the ladder is 6 ft from the wall?
9. Use substitution $u=1+x^2$ to evaluate the integral $$\int \sqrt{1+x^2} x^5 dx.$$
10. (a) State the definition of the definite integral $\int _a^bf(x)dx$ and illustrate the construction with a sketch. (b) Use the definition to justify that $\int _a^bcf(x)dx=c\int _a^bf(x)dx$ for a constant $c$.