This site is being phased out.
Applications of differential calculus
Contents
- 1 Solving equations numerically: bisection and Newton's method
- 2 How to compare functions, L'Hopital's Rule
- 3 Linearization
- 4 The accuracy of the best linear approximation
- 5 Flows: a discrete model
- 6 Motion under forces
- 7 Differential equations
- 8 Functions of several variables
- 9 Optimization examples
Solving equations numerically: bisection and Newton's method
Given a function $y=f(x)$, find such a $d$ that $f(d)=0$.
Algebraic methods only apply to a very narrow class of functions (such as polynomials of degree below $5$). What about a numerical solution? Solving the equation numerically means finding a sequence of numbers $d_n$ such that $d_n\to c$. Then $d_n$ are the approximations of the unknown $d$.
Let's recall how we interpreted the proof of the Intermediate Value Theorem as an iterated search for a solution of the equation $f(x)=0$. We constructed a sequence of nested intervals by cutting intervals in half. It is called bisection.
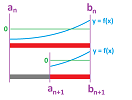
We have a function $f$ is defined and is continuous on interval $[a,b]$ with $f(a)<0,\ f(b)>0$ and we want to approximate a $d$ in $[a,b]$ such that $f(d) = 0$. We start with the halves of $[a,b]$: $\left[ a,\frac{1}{2}(a+b) \right],\ \left[ \frac{1}{2}(a+b),b \right]$. For at least one of them, $f$ changes its sign; we call this interval $[a_1,b_1]$.
Next, we consider the halves of this new interval and so on. We continue with this process and the result is two sequences of numbers.
Exercise. Write a recursive formula for these intervals.
These two sequences of numbers form a sequence of intervals: $$[a,b] \supset [a_1,b_1] \supset [a_2,b_2] \supset ...,$$ on each of which $f$ changes its sign: $$f(a_n)<0,\ f(b_n)>0\quad \text{ or }\quad f(a_n)>0,\ f(b_n)<0.$$ We concluded that the sequences converge to the same value, $a_n\to d,\ b_n\to d$, and, furthermore, from the continuity of $f$, we concluded that $$f(a_n)\to f(d),\ f(b_n)\to f(d).$$ Thus $d$ is an (unknown) solution: $f(d)=0$.
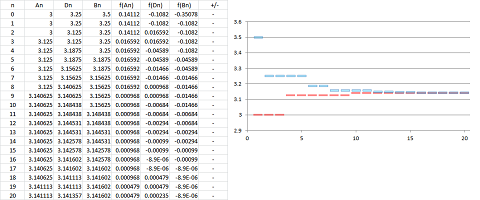
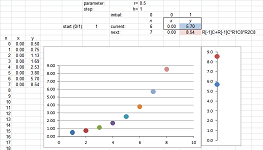
Example. Let's review how the bisection method solves a specific equation: $$\sin x=0.$$ We started with the interval $[a_1,b_1]=[3,3.5]$ and used the spreadsheet formula for $a_n$ and $b_n$: $$\texttt{=IF(R[-1]C[3]*R[-1]C[4]<0,R[-1]C,R[-1]C[1])},$$ $$\texttt{=IF(R[-1]C[1]*R[-1]C[2]<0,R[-1]C[-1],R[-1]C)}.$$
The values of $a_n,\ b_n$ visibly converge to $\pi$ (and so does $d_n$, the mid-point of the interval) while the values of $f(a_n),\ f(b_n)$ converge to $0$. $\square$
There are other methods for solving $f(x)=0$. One is to use the linearization of $f$ as a substitute, one such approximation at a time.
Suppose a function $f$ is given as well as the initial estimate $x_0$ of a solution $d$ of the equation $f(x)=0$. We replace $f$ in this equation with its linear approximation $L$ at this initial point: $$L(x)=f(x_0)+f'(x_0)(x-x_0).$$ Then we solve the equation $L(x)=0$ for $x$: $$L(x)=f(x_0)+f'(x_0)(x-x_0)=0.$$ In other words, we find the intersection of the tangent line with the $x$-axis:
The equation, which is linear, is easy to solve. The point of intersection is $$x_1=x_0-\frac{f(x_0)}{f'(x_0)}.$$ Then we repeat the process for $x_1$. And so on...
This is called Newton's method. It is a sequence of numbers given recursively: $$x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.$$
Warning: the method fails when it reaches a point where the derivative is equal to (or even close to) $0$.
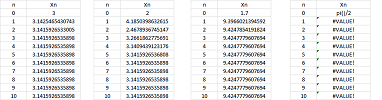
Example. Let's use Newton's method to solve the same equation as above: $$\sin x=0.$$ We start with $x_0=3$ and use the spreadsheet formula for $x_n$: $$\texttt{=R[-1]C-SIN(R[-1]C)/COS(R[-1]C)}.$$
The sequence converges to $\pi$ very quickly (left). However, as our choice of $x_0$ approaches $\pi /2$, the value of $x_1$ becomes larger and larger. In fact, it might be so large that the sequence won't ultimately converge to $\pi$ but to $2\pi,\ 100\pi$, etc. If we choose $x_0=\pi /2$ exactly, the tangent line is horizontal, failure... $\square$
Exercise. Solve the equation $\sin x=.2$.
How to compare functions, L'Hopital's Rule
How does one compare the “power” of two functions?
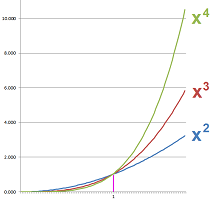
When they are power functions, say $x$ and $x^2$, or $x^2$ and $x^3$, the answer is known: the higher the power the stronger the function.
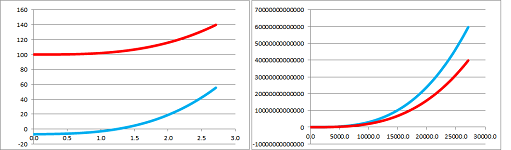
Same rule applies to polynomials. What about functions in general? What we learn from the power functions is that we don't look at the difference of two functions, $$(x^2+x)-x^2\to +\infty \text{ as } x\to +\infty,$$ but the ratio: $$\frac{x^2+x}{x^2}\to 1 \text{ as } x\to +\infty.$$
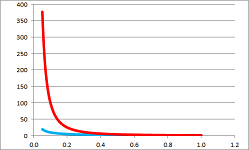
Example. We have encountered this problem indirectly many times when computing limits at infinity of rational functions. The method we used was to divide both numerator and denominator by the highest available power; for example: $$\begin{array}{lll} \frac{3x^3+x-7}{2x^3+100}&=\frac{3x^3+x-7}{2x^3+100}\frac{/x^3}{/x^3}\\ &=\frac{3+x^{-2}-7x^{-3}}{2+100x^{-3}}\\ &\to \frac{3}{2}& \text{ as } x\to \infty. \end{array}$$ We conclude that these two functions have the “same power” at infinity. We can see how they stay together below:
Even though the difference goes to infinity, the proportion remains visibly $3$ to $2$.
However, if we replace the power of the numerator with $4$, we see this: $$\begin{array}{lll} \frac{3x^4+x-7}{2x^3+100}&=\frac{3x^4+x-7}{2x^3+100}\frac{/x^4}{/x^4}\\ &=\frac{3+x^{-3}-7x^{-4}}{2x^{-1}+100x^{-4}}\\ &\to \infty& \text{ as } x\to \infty. \end{array}$$ We conclude that $3x^4+x-7$ is “stronger” at infinity than $2x^3+100$. We can see how quickly the former runs away below:
$\square$
Thus to compare two functions $f$ and $g$, at infinity or at a point, we form a fraction from them and evaluate the limit of the ratio: $$\lim \frac{f(x)}{g(x)}=?$$
Definition. If the limit below is infinite, or its reciprocal is zero, $$\lim \left|\frac{f(x)}{g(x)}\right|=\infty,\ \lim \left|\frac{g(x)}{f(x)}\right|=0,$$ we say that $f$ is of higher order than $g$, and use the following notation: $$f>>g\ \text{ and }\ g=o(f).$$ The latter reads “little o”.
The most important use of the latter notation is in the definition of the derivative: $$f'(a)=\lim_{\Delta x\to 0}\frac{\Delta y}{\Delta x}.$$ It can be rewritten as: $$\begin{array}{|c|}\hline \quad \Delta y=f'(a)\Delta x+o(\Delta x). \quad \\ \hline\end{array}$$
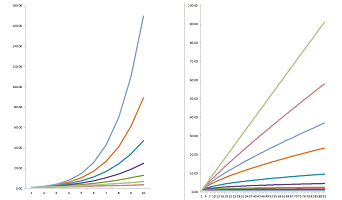
The method presented above allows us to justify the following hierarchy: $$...>>x^n>>...>>x^2>>x>>\sqrt{x}>>\sqrt[3]{x}>>...>>1.$$ Below, we see powers below $1$ on right and above $1$ on left:
Among polynomials, the degree plays the role of the order.
Theorem. For any two polynomials $P$ and $Q$, $\deg P<\deg Q$ if and only if $P=o(Q)$.
Exercise. Prove the theorem.
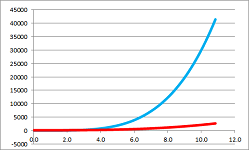
Next, where does $e^x$ fit in this hierarchy? Below, we compare $e^x$ and $x^{100}$:
The former seems stronger but, unfortunately, the methods of dividing by the higher power doesn't apply here. We will be looking for another method.
The idea of using limits to determine the relative “order” of functions also applies to their behavior at a point.
Example. Consider these functions are $0$: $$\frac{3+x^{-2}-7x^{-3}}{2+10x^{-3}}\to -\frac{7}{10} \text{ as } x\to 0.$$ We conclude that these two functions have the “same order” at $0$. However, below the numerator is of higher order at $0$ than the denominator: $$\frac{3+x^{-2}-7x^{-4}}{2+10x^{-3}}\to \infty \text{ as } x\to 0.$$ $\square$
We are thus able to justify the following hierarchy at $0$: $$...>>\frac{1}{x^n}>>...>>\frac{1}{x^2}>>\frac{1}{x}>>\frac{1}{\sqrt{x}}>>\frac{1}{\sqrt[3]{x}}>>...>>1.$$ Below, we compare $1/x$ and $1/x^2$:
However, the method fails for other types of functions: where does $\ln x$ fit in this hierarchy? We need a new approach...
Let's observe that the order of a function is determined by its rate of growth, i.e., its derivative. So, to compare two functions, we can try to compare their derivatives instead. After all, the derivative is a limit, by definition. We have computed so many derivatives by now that we can use the results to evaluate some other limits.
We can justify this idea for the following simplified case:
- $f(c)=g(c)=0$;
- $g'(c)\neq 0$.
Then $$\frac{f(x)}{g(x)} = \frac{f(x)-0}{g(x)-0}= \frac{f(x)-f(c)}{g(x)-g(c)} =\frac{\frac{f(x)-f(c)}{x-c}}{\frac{g(x)-g(c)}{x-c} }\to \frac{f'(c)}{g'(c)} \text{ by QR.}$$
Theorem (L'Hopital's Rule). Suppose functions $f$ and $g$ are continuously differentiable. Then, for limits of the types: $$x\to \infty \text{ and } x\to a^\pm,$$ we have $$\lim \frac{f(x)}{g(x)} = \lim\frac{f'(x)}{g'(x)}$$ if the latter exists, and provided the left-hand side is an indeterminate expression: $$\lim f(x) = \lim g(x) = 0, $$ or $$\lim f(x) = \lim g(x) = \infty.$$
An informal explanation why this works is that the denominators cancel below: $$\frac{\frac{\Delta f}{\Delta x}}{\frac{\Delta g}{\Delta x}}=\frac{\Delta f}{\Delta g}.$$
Warning: L'Hopital's Rule is not the Quotient Rule (of limits or of derivatives)!
Example. Compute $$\lim_{x \to \infty} \frac{x^{2} - 3}{2x^{2} - x + 1}.$$ The old method was to divide by the highest power. Instead, we apply L'Hopital's Rule: $$=\lim_{x \to \infty} \frac{2x}{4x-1}.$$ This is still indeterminate! So, apply LR again: $$=\lim_{x \to \infty} \frac{2}{4} = \frac{1}{2}.$$ $\square$
Warning: Before you apply L'Hopital's Rule verify that this is indeed an indeterminate expression.
Example. Compute $$\begin{array}{lll} \lim_{x\to 1} \frac{\ln x}{x-1} &&\leadsto\frac{0}{0}!\\ &=\lim_{x \to 1} \frac{\frac{1}{x}}{1} \\ &= \lim_{x \to 1} \frac{1}{x} \\ &= 1. \end{array}$$ $\square$
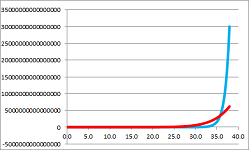
Example. Compute $$\begin{array}{lll} \lim_{x\to \infty}\frac{e^{x}}{x^{2}} && \leadsto\frac{\infty}{\infty}& \text{ ...apply LR}\\ &=\lim_{x\to\infty} \frac{e^{x}}{2x} & \leadsto\frac{\infty}{\infty} & \text{ ...apply LR}\\ &=\lim_{x \to \infty} \frac{e^{x}}{2} \\ &= \infty. \end{array}$$ $\square$
In fact, no matter how high the power is, it comes to zero after a sufficient number of differentiations. Meanwhile, nothing happens to the exponent: $$\lim_{x \to \infty} \frac{e^{x}}{x^{n}} = \infty. $$ Therefore, we have our hierarchy appended: $$e^x>>...>>x^n>>...>>x^2>>x>>\sqrt{x}>>\sqrt[3]{x}>>...>>1.$$
What about other indeterminate expressions? Below are the possible types of limits that correspond to algebraic operations:
- products:
$$0\cdot\infty;$$
- differences:
$$\infty - \infty;$$
- powers:
$$0^{0},\ \infty^{0},\ 1^{\infty}.$$ Idea: convert them to fractions.
Example. Evaluate: $$\lim_{x\to 0^{+}} x \ln x=?$$ How do we apply LR here? We convert to a fraction by dividing by the reciprocal: $$\begin{array}{lll} = \lim_{x\to 0^{+}} \frac{\ln x}{\frac{1}{x}} & \leadsto \frac{\infty}{\infty} \\ = \lim_{x \to 0^{+}} \frac{\frac{1}{x}}{-\frac{1}{x^{2}}}\\ = \lim_{x\to 0^{+}} -x = 0. \end{array}$$ $\square$
Example. Evaluate $$\lim_{x \to \infty}x^{\frac{1}{x}}=?$$ How do we convert to a fraction? Use log! $$\ln x^{\frac{1}{x}} = \frac{1}{x}\ln x. $$ Then, we use the fact that $\ln$ is continuous (the “magic words”): $$\begin{aligned} \ln\left( \lim_{x \to \infty} x^{\frac{1}{x}} \right) & = \lim_{x \to \infty}\left(\ln x^{\frac{1}{x}}\right) \\ &= \lim_{x \to \infty} \left(\frac{1}{x}\ln x\right) \\ &= \lim_{x\to\infty}\frac{\ln x}{x} \qquad \leadsto \frac{\infty}{\infty} \\ &\ \overset{\text{LR}}{=\! =\! =}\ \lim_{x\to\infty}\frac{\frac{1}{x}}{1} = 0. \end{aligned}$$ Therefore, $$\lim_{x\to\infty} x^{\frac{1}{x}} = e^{0} = 1. $$ $\square$
Exercise. What property of limits we used at the end?
Exercise. Prove $x>>\ln x>>\sqrt{x}$ at $\infty$.
Exercise. Compare $\ln x$ and $\frac{1}{x^n}$ at $0$.
Example. The condition of the theorem that requires the ratio to be an indeterminate expression must be verified. What can happen otherwise is illustrated below. If we apply L'Hopital's Rule, we get the following: $$\lim_{x\to +\infty}\frac{1+\frac{1}{x}}{1+\frac{1}{x^2}}\ \overset{\text{LR?}}{=\! =\! =}\ \lim_{x\to +\infty}\frac{\left( 1+\frac{1}{x}\right)'}{\left( 1+\frac{1}{x^2}\right)'}=\lim_{x\to +\infty}\frac{-\frac{1}{x^2}}{-\frac{2}{x^3}}=\frac{1}{2}\lim_{x\to +\infty}x=+\infty.$$ But the Quotient Rule for limits is applicable here: $$\lim_{x\to +\infty}\frac{1+\frac{1}{x}}{1+\frac{1}{x^2}}\ \overset{\text{QR}}{=\! =\! =}\ \frac{\lim_{x\to +\infty}\left(1+\frac{1}{x}\right)}{\lim_{x\to +\infty}\left(1+\frac{1}{x^2}\right)}=\frac{1}{1}=1.$$ A mismatch! L'Hopital's Rule is inapplicable because the limits of the numerator and the denominator of the original fraction exist! Here is another example: $$\lim_{x\to 1}\frac{x^{2}}{x} \ \overset{\text{LR?}}{=\! =\! =}\ \lim_{x \to 1}\frac{2x}{1} = 2...$$ $\square$
Exercise. Describe this class of functions: $o(1)$.
Linearization
It is a reasonable strategy to answer a question that you don't know the answer to by answering instead another one -- reasonably close -- with a known answer.
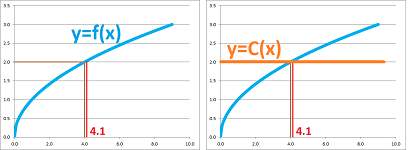
What is the square root of $4.1$? I know that $\sqrt{4}=2$, so I'll say that it's about $2$.
What is the square root of $4.3$? It's about $2$.
What is the square root of $3.9$? It's about $2$.
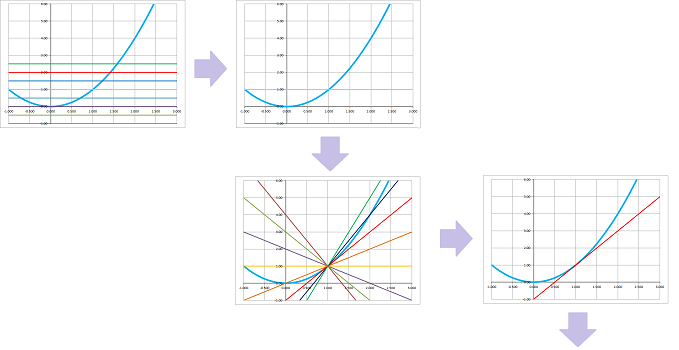
And so on. These are all reasonable estimates, but they are all the same! Our interpretation of this observation is that we approximate the function $f(x)=\sqrt{x}$ by a constant function $C(x)=2$.
It is a crude approximation!
The error of an approximation is the difference between the two functions, i.e., the function that gives us the lengths of these segments: $$E(x) = | f(x) - C | . $$ But what $C$ do we choose? Even though the choice is obvious, let's run through the argument anyway. We want to make sure that the error diminishes as $x$ is getting closer to $a$. In other words, we would like the following to be satisfied: $$E(x)=| f(x) - C |\to 0 \text{ as } x\to a,\ \text{ or } f(x) \to C \text{ as } x\to a.$$ It suffices to require that $f$ is continuous at $a$ if we choose $C=f(a)$!
As long as the number is “close” to $4$ we use it or we look for another number with a known square root. For example, $\sqrt{.99}\approx \sqrt{1}=1$, $\sqrt{10}\approx \sqrt{9}=3$, and so on.
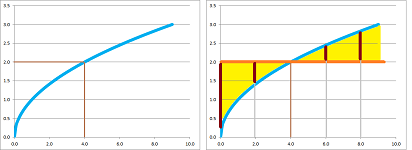
Can we do better that the horizontal line? Definitely!
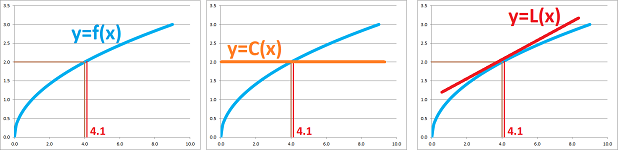
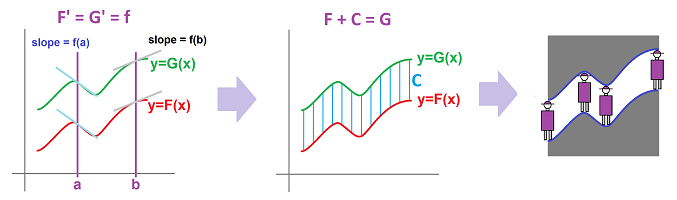
We already know that the tangent line “approximates” the graph of a function: when you zoom in on the point, the tangent line will merge with the graph:
There are many straight lines that can be used to approximate including the horizontal line and the tangent looks better!
What is so special about the tangent line?
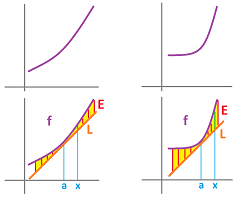
We are about to start using more precise language. Recall from Chapter 2 that the point-slope form of a line through $(x_0,y_0)$ with slope $m$ is given by (as a relation): $$ y - y_{0} = m(x - x_{0}). $$ Specifically, we have $$x_0=a,\ y_0=f(a).$$ Therefore, we have $$y-f(a)=m(x - a) .$$ At this point, we make an important step and stop looking at this as an equation of a line but as a formula for a new function: $$ L(x) = f(a) + m(x - a) .$$ It is linear polynomial (because the power of $x$ is $1$ while the rest of the parameters are constant). That's why it is called a linear approximation of $f$ at $x = a$.
Among these, however, when you zoom in on the point, the tangent line -- but no other line -- will merge with the graph. Indeed, the angle between the lines is preserved under magnification:
This is the geometric meaning of “best” approximation.
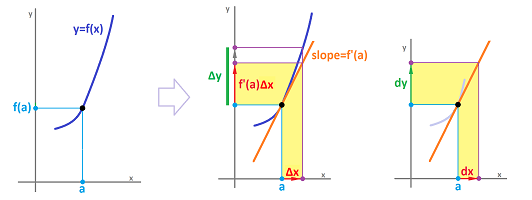
Now, algebra. Once again, let's look at the error, i.e., the difference between the two functions: $$E(x) = | f(x) -L(x) | . $$
For all of these approximations, we have, just as above, $$E(x)=| f(x) - L(x) |\to 0 \text{ as } x\to a.$$
Exercise. Prove this statement. Hint: use the “magic” words.
Then, how do we choose the “best” approximation? Will choose a function -- from among these -- with the error converging to $0$ the fastest possible. Specifically, we compare this convergence with that of the linear function: $$E(x)=| f(x) - L(x) |\to 0\ \text{ vs. }\ |x-a|\to 0.$$ We know how to compare the orders of convergence from our analysis of in the last section: look at the convergence of their ratio! Then, $E(x)$ converges faster if the limit of this ratio is zero; i.e., $$\frac{ f(x) -L(x) }{x-a}\to 0.$$ In other words, $$f(x) -L(x) =o(x-a).$$
Theorem (Best linear approximation). Suppose $f$ is differentiable at $x=a$ and $L(x)=f(a)+m(x-a)$ is any of its linear approximations. Then, $$\lim_{x\to a} \frac{ f(x) -L(x) }{x-a}=0 \Longleftrightarrow m=f'(a).$$
Proof. As $x\to a$, we have: $$\begin{array}{llcc} \frac{ f(x) -(f(a) + m(x-a)) }{x-a}&=&\frac{ f(x) -f(a)}{x-a} &-m \\ &\to& f'(a) &-m . \end{array}$$ $\blacksquare$
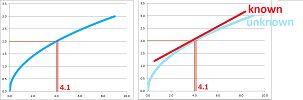
Example (root). Let's approximate $\sqrt{4.1}$.
We can't compute $\sqrt{x}$ by hand. In fact, the only meaning of $x=\sqrt{4.1}$ is that it is such a number that $x^2=4.1$. In that sense, the function $f(x)=\sqrt{x}$ is unknown.
With just a few exceptions such as $f(4)= \sqrt{4}=2$, etc. We will use these points as “anchors”. Then, we can use the constant approximation and declare that $\sqrt{4.1}\approx 2$.
The best linear approximation of $f$ is also known. The reason is that, as a linear function, it can be computed by hand. Let's find this function. $$\begin{aligned} f'(x) &= \frac{1}{2\sqrt{x}} \ \Longrightarrow \\ f'(4) &= \frac{1}{2\sqrt{4}} = \frac{1}{4}. \end{aligned}$$ The best linear approximation is: $$\begin{array}{lll} L(x) &= f(a) &+ f'(a) (x - a) \\ & = 2 &+ \frac{1}{4} (x - 4). \end{array} $$ This function is a replacement for $f(x)=\sqrt{x}$ in the vicinity of the “anchor point” $x=4$.
Next, $$\begin{aligned} L(4.1) &= 2 + \frac{1}{4}(4.1 - 4) \\ & = 2 + \frac{1}{4} \cdot 1 \\ & = 2 + 0.025 \\ & = 2.025. \end{aligned} $$ Thus, $2.025$ is an approximation of $\sqrt{4.1}$. $\square$
Exercise. Find the best linear approximation of $f(x)=x^{1/3}$ at $a=1$. Use it to estimate $1.1^{1/3}.$
Exercise. Use the best linear approximation of $f(x)=\sqrt{\sin x}$ to estimate $\sqrt{\sin \pi/2}$.
Replacing a function with its linear approximation is called linearization. Linearizations make a lot of things much simpler.
Example (integration). Linearization helps with integration. If we imagine that we don't know the antiderivative of $\sin x$, we can still make progress: $$\int \sin x\, dx\approx \int x\, dx=\frac{x^2}{2}+C.$$
In fact, the result is the quadratic approximation of $\cos x$! $\square$
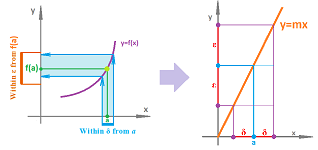
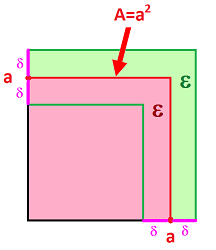
Example (limits). Not only all linear functions, $L(x)=mx+b,\ m\ne 0$, are continuous but also the relation, in the definition of continuity, between $\varepsilon$ and $\delta$ is very simple: to ensure $$|x-a|<\delta \Longrightarrow |L(x)-L(a)|<\varepsilon,$$ we simply choose: $$\delta=\tfrac{1}{m}\varepsilon.$$
We now interpret these two, as before:
- $\delta$ is the accuracy of the measurement of $x$ and
- $\varepsilon$ is the accuracy of the indirect evaluation of $y=L(x)$.
$\square$
Now, if $L$ is a linearization of function $y=f(x)$ around $a$, we can have a similar, approximate, analysis for $f$: we can make $\Delta f=f(a+\Delta x)-f(a)$ as small as we like by choosing $\Delta x$ small enough.
How do we find this $\Delta x$? We linearize: $$f'(a)=\frac{dy}{dx}\Bigg|_{x=a}\approx \frac{\Delta y}{\Delta x}.$$ Then, the change of the output variable is approximately proportional to the change of the input variable: $$\begin{array}{|c|}\hline \quad \Delta y\approx f'(a) \Delta x. \quad \\ \hline\end{array}$$ How well this approximation works is discussed in the next section. This idea can also be expressed via the differentials: $$\begin{array}{|c|}\hline \quad dy= f'(a) dx. \quad \\ \hline\end{array}$$ The equation is, in fact, their definition.
Example (error estimation). Let's revisit the example of evaluating the area $A=f(x)=x^2$ of square tiles when their dimensions are close to $10\times 10$.
Suppose the desired accuracy of $A$ is $\Delta A =5$, what should be the accuracy $\Delta x$ of measurement $x$? By trial-and-error, we discovered that $\Delta x=.2$ is appropriate: $$\begin{array}{lll} A&=(10 \pm .2)^2\\ &=10^2 \pm 2 \cdot 10 \cdot .2 +.2^2 \\ &\text{or }100.04 \pm 4. \end{array}$$ Instead, to get a quick “ballpark” figure, we find the derivative, $2x$, of $f(x)=x^2$ at $x=10$: $$f'(10)=2\cdot 10=20,$$ and then apply the above formula: $$\Delta A\approx f'(10) \Delta x=20\Delta x \ \Longrightarrow\ \Delta x \approx 5/20=.25.$$ So, in order to achieve the accuracy of $4$ square inches of the computation of the area of a $10\times 10$ tile, one will need the $1/4$-inch accuracy of the measurement of the side of the tile. $\square$
Exercise. What is the accuracy of the computation of the surface area of the Earth if the radius is found to be $6,360\pm 30$ kilometers? What about the volume?
Example. With enough “anchor” points, we can produce an approximation of the whole, unknown, function. The result for $f(x)=\sqrt{x}$ is shown below:
$\square$
As a summary, below we illustrate how we attempt to approximate a function around the point $(1,1)$ with constant functions first; from those we choose the horizontal line through the point. This line then becomes one of many linear approximations of the curve that pass through the point; from those we choose the tangent line.
In Chapter 15, we will see that these are just the two first steps in the sequence of approximations...
The accuracy of the best linear approximation
An “approximation” is meaningless if it comes as a single number.
We need to know more about what we have to make this number useful. How close is $3.14$ to $\pi$? Even more important is the question: how close is $\pi$ to $3.14$? Or, from the last section, how close is $\sqrt{4.1}$ to $2.025$? The answer to the question will give $\sqrt{4.1}$ an exclusive range of possible values.
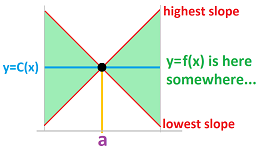
First, the constant approximation. Even though the function $y=f(x)$ coincides with $y=C=f(a)$ at $x=$, it may run away very fast and very far afterwards. How far? The only limit is the rate of growth of $f$, i.e., its derivative! So, we can predict the behavior of $f$ if we have a priori information about $|f'|$. Then we have a range of possible values for $f(x)$, for all $x$! The result is a funnel that contains the (unknown) graph of $y=f(x)$:
Indeed, we can conclude from the Mean Value Theorem that $$|f(x)-C(x)|=|f(x)-f(a)| =|f'(t)(x-a)|\le K|x-a|,$$ if we only know that $|f'(t)|\le K$ for all $t$ between $a$ and $x$.
Example. How close is $\sqrt{4.1}$ to $2$? We estimate the derivative of $f(x)=\sqrt{x}$: $$f'(t)=\frac{1}{2\sqrt{t}}\le\frac{1}{2\sqrt{4}}\le .25.$$ Then $$|\sqrt{4.1}-2|\le .25|4.1-4|=.025.$$ $\square$
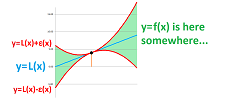
Next, the linear approximation. Two graphs below have the same tangent line but one is better approximated. What causes the difference?
There are slopes close to our location that are very different from that of the tangent line. The quantity that makes the slopes, i.e., the derivatives, change is the second derivative. We can then predict the accuracy of the approximation if we have a priori information about the magnitude of the second derivative.
Theorem (Error bound). Suppose $f$ is twice differentiable at $x=a$ and $L(x)=f(a)+f'(a)(x-a)$ is its best linear approximation at $a$. Then, $$E(x)=|f(x)-L(x)| \le \tfrac{1}{2}K(x-a)^2,$$ where $K$ is a bound of the second derivative on the interval from $a$ to $x$: $$|f' '(t)|\le K \text{ for all } t \text{ in this interval}.$$
The theorem claims that $E=o((x-a)^2)$.
When $K$ is fixed, we have a range of possible values of the function $y=f(x)$! The result is, again, a funnel that contains the (unknown) graph of $y=f(x)$:
This time, the two edges of the funnel are parabolas: $$y=L(x)\pm\frac{1}{2}K(x-a)^2.$$ Therefore, the value of $K$ makes the funnel wider or narrower.
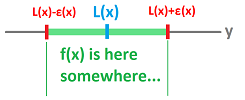
The practical meaning of the theorem is the following. For each $x$, this error bound, $$\varepsilon (x)= \tfrac{1}{2}K(x-a)^2,$$ is the accuracy of the approximation in the sense that the interval located on the $y$-axis $$[L(x)-\varepsilon (x),L(x)-\varepsilon (x)]$$ contains the true number, $f(x)$.
This interval is a vertical cross-section of the funnel.
Example (root). We continue with the last example: $$\sqrt{4.1}\approx L(4.1)=2.025.$$ Once again, the answer is unsatisfactory because it doesn't really tell us anything about the true value of $\sqrt{4.1}$. In fact, $\sqrt{4.1}\ne 2.025$! Let's apply the theorem. First, we find the second derivative: $$\begin{aligned} f(x) &= \sqrt{x} \ \Longrightarrow f'(x) = \frac{1}{2\sqrt{x}} \ \Longrightarrow \\ f' '(x) &= \left( \frac{1}{2\sqrt{x}} \right)'=\left( \frac{1}{2} x^{-1/2} \right)' \quad\text{ by PF}\\ &=\frac{1}{2} \left( -\frac{1}{2} \right) x^{-1/2-1}\\ &=-\frac{1}{4} x^{-3/2}. \end{aligned}$$ So, we need a bound for this function: $$|f' '(x)|=\tfrac{1}{4}\left|x^{-3/2}\right|$$ over the interval $[4,4.1]$. This is a simple, decreasing function.
Therefore, $$|f' '(x)|\le |f' '(4)|=\tfrac{1}{4}\left|4^{-3/2}\right|=\tfrac{1}{32}=0.03125.$$ This is our best choice for $K$! According to the theorem, our conclusion is that the error of the approximation cannot be larger than the following: $$E(x)=|f(x)-L(x)| \le \tfrac{1}{2}0.03125\cdot (x-4)^2.$$ Specifically, $$E(4.1)=\left|\sqrt{4.1}-L(4.1)\right| \le \tfrac{1}{2}0.03125\cdot (4.1-4)^2,$$ or $$\left|\sqrt{4.1}-2.025\right| \le 0.00015625.$$ Therefore, we conclude:
- $\sqrt{4.1}$ is within $\varepsilon = 0.00015625$ from $2.025$.
In other words, we have: $$2.025 - 0.00015625\le \sqrt{4.1}\le 2.025 +0.00015625,$$ or $$2.02484375 \le \sqrt{4.1} \le 2.02515625.$$ We have found an interval that is guaranteed to contain the number we are looking for! $\square$
Example (sin). Approximate $\sin .01$. Note that the constant approximation is $\sin .01 \approx \sin 0 =0$. So, we have $a=0$. Now we compute: $$\begin{array}{lll} f(x)=\sin x& \\ f'(x)=\cos x& \Longrightarrow& L(x)=0+\cos x \Big|_{x=0}(x-0)&\Longrightarrow& L(x)=x\\ f' '(x)=-\sin x& \Longrightarrow & |f' '(x)|=\sin x& \Longrightarrow &|f' '(x)|\le 1=K. \end{array}$$ Thus, $$\sin .01 \approx .01,$$ and, furthermore, the accuracy is at worst $$\varepsilon = \tfrac{1}{2}K(x-a)^2=.5\cdot 1\cdot .01^2=.00005.$$ Therefore, $$.01-.00005=.00995\le \sin.01 \le .01005 =.01+.00005.$$
Note that the choice of $K$ in the last example was best possible. This was, therefore, a worst-case scenario. In contrast, here $K=1$ isn't the best possible choice. By limiting our attention to the relevant part of the graph of $|f' '|$ we discover a better value for the bound $K=.01$. This improves the accuracy by a factor of $.01$. $\square$
Knowing the concavity of the function that we approximate cuts the funnel in half.
Corollary (One-sided error bound). Suppose $f$ is twice differentiable at $x=a$ and $L(x)=f(a)+f'(a)(x-a)$ is its best linear approximation at $a$. Suppose also that $|f' '(x)|\le K$ for all $x$ in $[a,b]$. Then,
- when $f$ is concave up (i.e., $f' '>0$), we have for each $x$ in $[a,b]$:
$$L(x)\le f(x) \le L(x)+\tfrac{1}{2}K(x-a)^2;$$
- when $f$ is concave down (i.e., $f' '<0$), we have for each $x$ in $[a,b]$:
$$L(x)-\tfrac{1}{2}K(x-a)^2\le f(x) \le L(x).$$
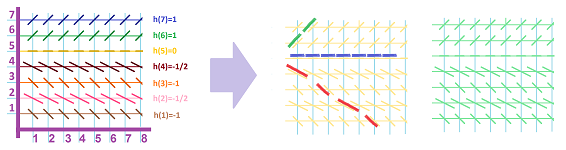
Flows: a discrete model
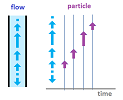
Previously, we considered an example of how functions appear as direct representations of the dynamics given by an indirect description: motion's velocity is derived from the acceleration and then the location from the velocity. The acceleration (or the force) is a function of time and so is the velocity. A different, and just as important, example of such emergence is flows of liquids. However, here the velocity is a function of location.
We start with a discrete model.
Suppose there is a pipe with the velocity of the stream measured somehow at each location. Similarly, this is a canal with the water that has the exact same velocity -- parallel to the canal -- at all locations across it. In other words, the velocity only varies along the length of the pipe or the canal. This makes the problem one-dimensional.
Problem: Trace a single particle of this stream.
We will simply apply the familiar formula to compute the location from the velocity.
A fixed time increment $\Delta t$ is supplied ahead of time even though it can also be variable.
We start with the following two quantities provided by the model we are to implement:
- the initial time $t_0$, and
- the initial location $p_0$.
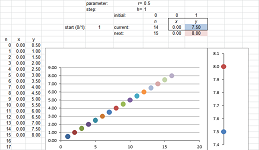
They are placed in the first row of the spreadsheet; for example: $$\begin{array}{c|c|c|c} &\text{iteration } n&\text{time }t_n&\text{velocity }v_n&\text{location }p_n\\ \hline \text{initial:}&0&3.5&--&22\\ \end{array}$$ This is the starting point. We would like to know the values of these quantities at every moment of time, in these increments.
As we progress in time and space, new numbers are placed in the next row of our spreadsheet. This is how the second row, $n=1,\ t_1=t_0+\Delta t$, is finished.
The current velocity $v_1$ given in the first cell of the row and the initial location $p_0$ is the last cell of the last row. The following recursive formula is placed in the second cell of the new row of our spreadsheet:
- next location $=$ initial location $+$ current velocity $\cdot$ time increment.
This dependence is shown below for $\Delta t=.1$: $$\begin{array}{c|c|ccccc} &\text{iteration } n&\text{time }t_n&&\text{velocity }v_n&&\text{location }p_n\\ \hline \text{initial:}&0&t_0=3.5&&--&&p_0=22\\ &&\downarrow&&&\swarrow&\downarrow\\ &1&t_1=3.5+.1&\to&v_1=33&\to&p_1=22+33\cdot .1\\ &&\downarrow&&&\swarrow&\downarrow\\ &2&t_2=?&\to&v_2=?&\to&p_2=?\\ \end{array}$$ Also, in a flow, the current velocity of a particle depends -- somehow -- on the current time or its (last) location, as indicated by the arrows. This dependence may be an explicit formula or it may come from the instruments readings.
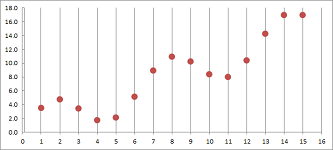
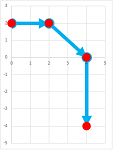
We continue with the rest in the same manner. As we progress in time and space, a number is supplied and are placed in each of the columns of our spreadsheet one row at a time: $$t_n,\ v_n,\ p_n,\ n=1,2,3,...$$ We then plotting the time and location on the plane with axes $t$ (horizontal) and $p$ (vertical). The result is a sequence of points developing one row at a time that might looks like this:
The first quantity in each row we compute is the time:
- next moment of time $=$ last moment of time $+$ time increment,
- $t_{n+1}=t_n+\Delta t$.
The next is the velocity $v_{n+1}$ which may be constant or may explicitly depend on the values in the previous row.
The $n$th iteration of the location $p_n$ is computed:
- next location $=$ last location $+$ current velocity $\cdot$ time increment,
- $p_{n+1}=p_n+v_{n+1}\cdot \Delta t$.
The values of the location are placed in the third column of our spreadsheet.
The result is a growing table of values: $$\begin{array}{c|c|c|c|c|c} &\text{iteration } n&\text{time }t_n&&\text{velocity }v_n&\text{location }p_n\\ \hline \text{initial:}&0&3.5&&--&22\\ &1&3.6&&33&25.3\\ &...&...&&...&...\\ &1000&103.5&&4&336\\ &...&...&&...&...\\ \end{array}$$ The result may be seen as three sequences $t_n,\ v_n,\ p_n$ or as the table of values of two functions of $t$. The result might look like this:
Let's implement this algorithm with a spreadsheet.
Example. Suppose that the velocity of the stream is constant: $$v_{n+1}=.5.$$
$\square$
Exercise. Find the recursive formula for the position.
Example. Suppose that there is a source of water in the middle of the pipe and the velocity of the stream is directly proportional to the distance from the source: $$v_{n+1}=.5\cdot p_n.$$
$\square$
Exercise. Find the recursive formula for the position.
Exercise. Modify the formulas for the case of a variable time increment: $\Delta t_{n+1}=t_{n+1}-t_n$.
What about a continuous flow?
We can imagine that the object moves from a given location to the next following a straight line. This does make the motion continuous. However, what if it is the relation between the position and the velocity that that holds continuously?
More precisely, we pose the following:
- Problem: suppose the velocity comes from an explicit formula as a function of the location $z=f(y)$ defined on an interval $J$, is there an explicit formula for the location as a function of time $y=y(t)$ defined on an interval $I$?
We assume that there is a version of our recursive relation, $$p_{n+1}=p_n+v_{n+1}\cdot \Delta t,$$ for every $\Delta t>0$ small enough. Then our two functions have to satisfy: $$v_n=f(p_n) \text{ and } p_n=y(t_n).$$
We substitute these two, as well as $t=t_n$, into the recursive formula for $p_{n+1}$: $$y(t+\Delta t)=y(t)+f(y(t+\Delta t))\cdot \Delta t.$$ Then, $$\frac{y(t+\Delta t)-y(t)}{\Delta t}=f(y(t+\Delta t)).$$ Taking the limit over $\Delta t\to 0$ gives us the following: $$y'(t)=f(y(t)),$$ provided $y=y(t)$ is differentiable at $t$ and $z=f(y)$ is continuous at $y(t)$. The above result is called a differential equation. Such equations are considered below and throughout the rest of the text.
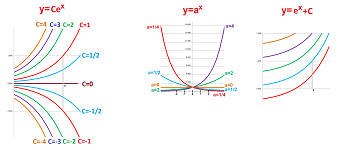
Example. Let's again consider the case when the velocity is proportional to the location: $$v_{n+1}=.5\cdot p_n.$$ For the continuous case, we have a differential equation: $$y'=.5\cdot y.$$ We already know its solution: $$y(t)=Ce^{.5t},$$ for any $C$. $\square$
Now a flow on the plane. In that case, we only show the two spatial coordinates and hide the time:
Instead of two (velocity -- location), there will be four main columns when the motion is two-dimensional and six when it is three-dimensional: $$\begin{array}{c|c|cc|cc|c} \text{}&\text{time}&\text{horiz.}&\text{horiz.}&\text{vert.}&\text{vert.}&...\\ \text{} n&\text{}t&\text{vel. }x'&\text{loc. }x&\text{vel. }y'&\text{loc. }y&...\\ \hline 0&3.5&--&22&--&3&...\\ 1&3.6&33&25.3&4&3.5&...\\ ...&...&...&...&...&...&...\\ 1000&103.5&4&336&66&4&...\\ ...&...&...&...&...&...&...\\ \end{array}$$
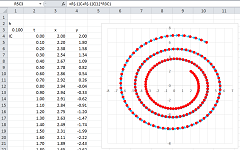
Example. Suppose the velocity of the flow depends on the location. In fact, let the velocity be proportional to the location: $$v_{n+1}=.2\cdot p_n,$$ for both horizontal and vertical. This is the result:
The particles are flying away from the center. For more complex patterns, the vertical and horizontal will have to be interdependent. For example, the horizontal velocity may be proportional to the vertical location and the vertical velocity proportional to the negative of the horizontal location:
$\square$
Motion under forces
The concepts introduced above allow us to state some elementary facts about the Newtonian physics, in dimension $1$.
All functions are functions of time.
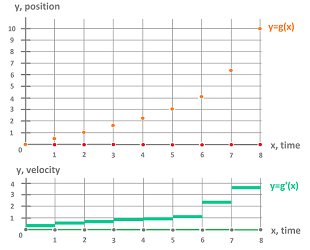
The main quantities are the following: $$\begin{array}{lllll} \text{quantity }&\text{incremental }&\text{nodes }&\text{continuous }\\ \hline \text{location: }&r&\text{ primary }&r&\\ \text{displacement: }&D=\Delta r&\text{ secondary }&D=dr&\\ \text{velocity: }&v=\frac{\Delta r}{\Delta t}&\text{ secondary }&v=r'&\\ \text{momentum: }&&\text{ secondary }&p=mv&\\ \text{impulse: }&J=\Delta p&\text{ primary }&J=dp&\\ \text{acceleration: }&a=\frac{\Delta^2 r}{\Delta t^2}&\text{ primary }&a=r' '& \end{array}$$
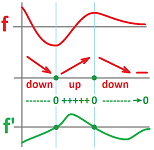
For example, the upward concavity of the function below is obvious, which indicates a positive acceleration:
Newton's First Law: If the net force is zero, then the velocity $v$ of the object is constant: $$F=0 \Longrightarrow v=\text{ constant }.$$
The law can be restated without invoking the geometry of time:
- If the net force is zero, then the displacement $dr$ of the object is constant:
$$F=0 \Longrightarrow dr=\text{ constant }.$$ The law shows that the only possible type of motion in this force-less and distance-less space-time is uniform; i.e., it is a repeated addition: $$r(t+1)=r(t)+c.$$
Newton's Second Law: The net force on an object is equal to the derivative of its momentum $p$: $$F=p'.$$
Newton's Third Law: If one object exerts a force $F_1$ on another object, the latter simultaneously exerts a force $F_2$ on the former, and the two forces are exactly opposite: $$F_1 = -F_2.$$
Law of Conservation of Momentum: In a system of objects that is “closed”; i.e.,
- there is no exchange of matter with its surroundings, and
- there are no external forces; $\\$
the total momentum is constant: $$p=\text{ constant }.$$
In other words, $$J=dp=0.$$ To prove, consider two particles interacting with each other. By the third law, the forces between them are exactly opposite: $$F_1=-F_2.$$ Due to the second law, we conclude that $$p_1'=-p_2',$$ or $$(p_1+p_2)'=0.$$
Exercise. State the equation of motion for a variable-mass system (such as a rocket). Hint: apply the second law to the entire, constant-mass system.
Exercise. Create a spreadsheet for all of these quantities.
To study this physics in dimension $2$ or $3$, one simply combines the three functions for each of the above quantities into one.
Suppose we know the forces affecting a moving object. How can we predict its dynamics?
Assuming a fixed mass, the total force gives us our acceleration. Then, we apply the same formula (i.e., anti-differentiation) to compute:
- the velocity from the acceleration, and then
- the location from the velocity.
We will examine a discrete model. As an approximation, it allows us to avoid anti-differentiation and rely entirely on algebra.
A fixed time increment $\Delta t$ is supplied ahead of time even though it can also be variable.
We start with the following three quantities that come from the setup of the motion:
- the initial time $t_0$,
- the initial velocity $v_0$, and
- the initial location $p_0$.
They are placed in the four consecutive cells of the first row of the spreadsheet: $$\begin{array}{c|c|c|c|c} &\text{iteration } n&\text{time }t_n&\text{acceleration }a_n&\text{velocity }v_n&\text{location }p_n\\ \hline \text{initial:}&0&3.5&--&33&22\\ \end{array}$$ Another quantity that comes from the setup is
- the current acceleration $a_1$.
It will be placed in the next row.
This is the starting point. We would like to know the values of all of these quantities at every moment of time, in these increments.
As we progress in time and space, new numbers are placed in the next row of our spreadsheet. This is how the second row, $n=1,\ t_1=t_0+\Delta t$, is completed.
The current acceleration $a_0$ given in the first cell of the second row. The current velocity $v_1$ is found and placed in the second cell of the second row of our spreadsheet:
- current velocity $=$ initial velocity $+$ current acceleration $\cdot$ time increment.
The second quantity we use is the initial location $p_0$. The following is placed in the third cell of the second row:
- current location $=$ initial location $+$ current velocity $\cdot$ time increment.
This dependence is shown below: $$\begin{array}{c|c|c|cccc} &\text{iteration } n&\text{time }t_n&\text{acceleration }a_n&&\text{velocity }v_n&&\text{location }p_n\\ \hline \text{initial:}&0&3.6&--&&33&&22\\ &&&& &\downarrow& &\downarrow\\ \text{current:}&1&t_1&66&\to&v_1&\to&p_1\\ \end{array}$$
These are recursive formulas just as in the last section.
We continue with the rest in the same manner. As we progress in time and space, numbers are supplied and placed in each of the four columns of our spreadsheet one row at a time: $$t_n,\ a_n,\ v_n,\ p_n,\ n=1,2,3,...$$
The first quantity in each row we compute is the time: $$t_{n+1}=t_n+\Delta t.$$ The next is the acceleration $a_{n+1}$ which may be constant (such as in the case of a free-falling object) or may explicitly depend on the values in the previous row.
Where does the current acceleration come from? It may come as pure data: the column is filled with numbers ahead of time or it is being filled as we progress in time and space. Alternatively, there is an explicit, functional dependence of the acceleration (or the force) on the rest of the quantities. The acceleration may depend on the following:
- 1. the current time, e.g., $a_{n+1}=\sin t_{n+1}$ such as when we speed up the car, or
- 2. the last location, e.g., $a_{n+1}=1/p_n^2$ such as when the gravity depends on the distance to the planet, or
- 3. the last velocity, e.g., $a_{n+1}=-v_n$ such as when the air resistance works in the opposite direction of the velocity,
or all three.
Exercise. Draw arrows in the above table to illustrate these dependencies.
Simple examples of case 1 and case 2 are addressed below and in the next section, respectively. More examples of case 1 are discussed in Chapter 11 and in the multidimensional setting in Chapter 17. Case 2 and case 3 are considered in Chapter 22.
The $n$th iteration of the velocity $v_n$ is computed:
- current velocity $=$ last velocity $+$ current acceleration $\cdot$ time increment,
- $v_{n+1}=v_n+a_n\cdot \Delta t$.
The values of the velocity are placed in the second column of our spreadsheet.
The $n$th iteration of the location $p_n$ is computed:
- current location $=$ last location $+$ current velocity $\cdot$ time increment,
- $p_{n+1}=p_n+v_n\cdot \Delta t$.
The values of the location are placed in the third column of our spreadsheet.
The result is a growing table of values: $$\begin{array}{c|c|c|c|c|c} &\text{iteration } n&\text{time }t_n&&\text{acceleration }a_n&\text{velocity }v_n&\text{location }p_n\\ \hline \text{initial:}&0&3.5&&--&33&22\\ &1&3.6&&66&38.5&25.3\\ &...&...&&...&...&...\\ &1000&103.5&&666&4&336\\ &...&...&&...&...&...\\ \end{array}$$ The result may be seen as four sequences $t_n,\ a_n,\ v_n,\ p_n$ or as the table of values of three functions of $t$.
Exercise. Implement a variable time increment: $\Delta t_{n+1}=t_{n+1}-t_n$.
Example (rolling ball). A rolling ball is unaffected by horizontal forces. Therefore, $a_n=0$ for all $n$. The recursive formulas for the horizontal motion simplify as follows:
- the velocity $v_{n+1}=v_n+a_n\cdot \Delta t=v_n=v_0$ is constant;
- the position $p_{n+1}=p_n+v_n\cdot \Delta t=p_n+v_0\cdot \Delta t$ grows at equal increments.
In other words, the position depends linearly on the time. $\square$
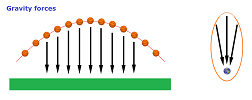
Example (falling ball). A falling ball is unaffected by horizontal forces and the vertical force is constant: $a_n=a$ for all $n$. The first of the two recursive formulas for the vertical motion simplifies as follows:
- the velocity $v_{n+1}=v_n+a_n\cdot \Delta t=v_n+a\cdot \Delta t$ grows at equal increments;
- the position $p_{n+1}=p_n+v_n\cdot \Delta t$ grows at linearly increasing increments.
In other words, the position depends quadratically on the time. $\square$
More interesting applications involve both vertical and horizontal components.
Instead of three (acceleration -- velocity -- location), there will six main columns when the motion is two-dimensional such as in the case of angled flight and nine when it is three-dimensional such as in the case of side wind: $$\begin{array}{c|c|ccc|ccc|c} \text{}&\text{time}&\text{horiz.}&\text{horiz.}&\text{horiz.}&\text{vert.}&\text{vert.}&\text{vert.}&...\\ \text{} &\text{}&\text{acceleration}&\text{velocity}&\text{position}&\text{acceleration}&\text{velocity}&\text{position}&...\\ \text{} n&\text{}t&a_n&v_n&x_n&b_n&u_n&y_n&...\\ \hline 0&3.5&--&33&22&-10&5&3&...\\ 1&3.6&66&38.5&25.3&-15&4&3.5&...\\ ...&...&...&...&...&...&...&...&...\\ 1000&103.5&666&4&336&14&66&4&...\\ ...&...&...&...&...&...&...&...&...\\ \end{array}$$
The shape of the trajectory is then unpredictable.
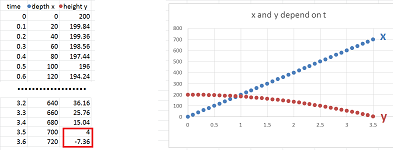
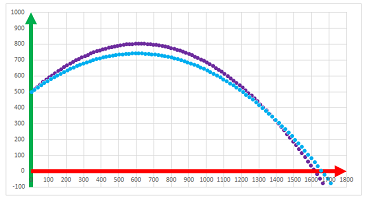
Example (cannon). A falling ball is unaffected by horizontal forces and the vertical force is constant: $$x:\ a_{n+1}=0;\quad y: b_{n+1}=-g.$$ Now recall the setup considered previously: from a $200$ feet elevation, a cannon is fired horizontally at $200$ feet per second.
The initial conditions are:
- the initial location, $x:\ x_0=0$ and $y:\ y_0=200$;
- the initial velocity, $x:\ v_0=200$ and $y:\ u_0=0$.
Then we have two pairs of recursive equations independent of each other: $$\begin{array}{lll} x:& v_{n+1}&=v_0, & &x_{n+1}&=x_n&+v_n\Delta t;\\ y:& u_{n+1}&=u_n&-g\Delta t, &y_{n+1}&=y_n&+u_n\Delta t. \end{array}$$
Implemented with a spreadsheet, the formulas produce the same results as the explicit formulas did before:
$\square$
Example ("solar" system). The gravity is constant (independent of location) in the free-fall model.
If we now look at the solar system, maybe the gravity is also constant?
The direction will, of course, matter!
$\square$
Differential equations
A differential equation is an equation that relates values of the derivative of the function to the function's values. To solve the equation is to find all possible functions that satisfy it.
Example. The simplest example of a differential equation is: $$f'(x)=0 \text{ for all } x.$$ We already know the solution:
- constant function are solutions, and, conversely,
- only constant functions are solutions.
$\square$
Example. We can replace $0$ with any function: $$f'(x)=g(x) \text{ for all } x.$$ We already know the solution:
- a solution $f$ has to be an antiderivative of $g$, and, conversely,
- only antiderivatives of $g$ are solutions.
$\square$
However, let's take a look at the problem with a fresh eye.
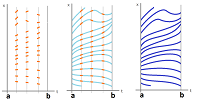
For the first kind of differential equation, we will be looking for functions $y=y(x)$ that satisfy the equation, $$y'(x)=g(x) \text{ for all } x.$$ What we know from the equation is the value of the derivative $y'(x)$ of $y$ at every point $x$ but we don't know the value $y(x)$ of the function itself. Then, for every $x$, we know the slope of the tangent line at $(x,y(x))$. As $y(x)$ is unknown, in order to visualize the data, we plot the same slope for every point $(x,y)$ on a given vertical line:
Thus, for each $x=c$, we indicate the angle $\alpha$, with $g(c)=\tan \alpha$, of the intersection of the graph of the unknown function $y=y(x)$ and the vertical line $x=c$.
Metaphorically, we are to create a fabric from two types of threads. The vertical ones have already been placed and the way the threads of the second type are to be weaved in has also been set.
The challenge is to devise a function that would cross these lines at these exact angles.
Is it always possible to have these functions? Yes, at least when $g$ is continuous. How do we find them? Anti-differentiation.
Example. A familiar interpretation is that of an object the velocity $v(x)=y'(x)$ of which is known at any moment of time $x$ and its location $y=y(x)$ is to be found.
These solutions fill the plane without intersections. They are just the vertically shifted versions of one of them. $\square$
For another kind of a differential equation, what if the derivative depends on the values of the function only (and not the values of the variable)?
We are looking for functions $y=y(x)$ that satisfy the equation, $$y'(x)=h(y(x)) \text{ for all } x.$$ What we know from the equation is the value of the derivative $y'(x)$ of $y$ at every point $(x,y)$ even though we don't know the value $y(x)$ of the function itself. Then, for every $y$, we know the slope of the tangent line at $(x,y)$. As $y(x)$ is unknown, in order to visualize the data, we plot the same slope for every point $(x,y)$ on a given horizontal line:
Thus, for each $y=d$, we indicate the angle $\alpha$, with $h(d)=\tan \alpha$, of the intersection of the graph of the unknown function $y=y(x)$ and the vertical line $x=c$ with $y(c)=d$.
Metaphorically, we are to create a fabric from two types of threads. The horizontal ones have already been placed and the way the threads of the second type are to be weaved in has also been set.
Is it always possible to have these functions? Yes, at least when $h$ is differentiable. The challenge is to devise a function that would cross these lines at these exact angles. How this can be done numerically is discussed later.
Example. An interpretation is a stream of liquid with its velocity known at every location $y$ and we need to trace the path of a particle initially located at a specific place $y_0$.
$\square$
Example. This is what happens when the velocity is equal to the location: $$y'=y.$$ To solve, what is the function equal to its derivative? It's the exponent $y=e^x$, of course. However, all of its multiples $y=Ce^x$ are also solutions:
These multiples of the exponent are shown on the left, not to be confused with the exponents of various bases (middle). Just as the differential equations of the first kind, these solutions fill the plane. $\square$
Exercise. What is the transformation of the plane that creates all these curves from one?
Exercise. Can the velocity be really “equal” to the location?
Exercise. What happens when the velocity is proportional to the location; i.e., $$y'=ky?$$
Compare and contrast: $$\begin{array}{lll} \text{DE: }&y'(x)=g(x)&y'(x)=h(y(x))\\ \hline \text{the slopes are the same along any }&\text{ vertical line }&\text{ horizontal line }\\ \text{the velocity is known at any }&\text{ time }&\text{ location }\\ \end{array}$$
Of course, differential equations are also common that have neither of these patterns:
Even though we can't solve those equations yet, once we have a family of curves, it is easy to find a differential equation it came from.
Example. What differential equation does the family of all concentric circles around $0$ satisfy?
This family is given by: $$x^2+y^2=r^2,\ \text{ real } r.$$ We simply differentiate the equation implicitly: $$x^2+y^2=r^2\ \Longrightarrow\ 2x+2yy'=0.$$ That's the equation. $\square$
Example. What about this family of hyperbolas?
This family is given by: $$xy=C,\ \text{ real } C.$$ Again, we differentiate the equation implicitly. We have: $$y+xy'=0.$$ $\square$
Functions of several variables
Optimization examples
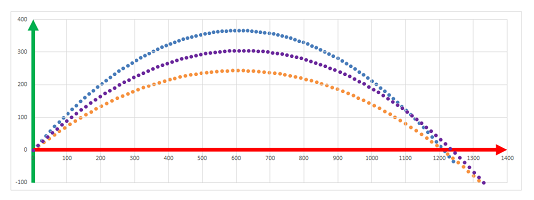
Example. In Chapter 7, we confirmed -- numerically -- that it is really true that $45$ degree is the best angle to shoot for longer distance:
Let's apply the methods of calculus to prove this fact. Recall the dynamics of this motion. The horizontal coordinate and the vertical coordinate are given by: $$\begin{cases} x&=x_0&+v_0t,\\ y&=y_0&+u_0t&-\tfrac{1}{2}gt^2, \end{cases}$$ with the following initial conditions:
- $x_0$ is the initial depth,
- $v_0$ is the initial horizontal component of velocity,
- $y_0$ is the initial height, and
- $u_0$ is the initial vertical component of velocity.
We shoot from the ground at zero depth: $x_0=y_0=0$. We assume that the initial speed is $1$ and that we shoot under angle $\alpha$. Then, $$\begin{cases} v_0&=&\cos \alpha,\\ u_0&=&\sin \alpha. \end{cases}$$ We substitute: $$\begin{cases} x&=&\cos \alpha\cdot t,\\ y&=&\sin \alpha\cdot t&-\tfrac{1}{2}gt^2. \end{cases}$$ The ground is reached at the moment $t$ when $y=0$, or $$\sin \alpha\cdot t-\tfrac{1}{2}gt^2=0.$$ We discard the starting moment, $t=0$, and end up with: $$\sin \alpha-\tfrac{1}{2}gt=0.$$ We solve for $t$, $$t=\frac{2}{g}\sin\alpha,$$ and substitute into the equation for $x$: $$x=\cos \alpha\cdot t=\cos \alpha\cdot \frac{2}{g}\sin\alpha.$$ This is the final distance, the depth of the shot: $$D(\alpha)=\frac{2}{g}\sin\alpha\cos \alpha.$$ We need to find the value of $\alpha$ that maximizes $D$. Since $D(0)=D(\pi/2)=0$, the answer lies within this interval. We differentiate: $$D'(\alpha)=\frac{2}{g}\big(\cos\alpha\cos \alpha+\sin\alpha(-\sin\alpha)\big)=\frac{2}{g}(\cos^2\alpha-\sin^2\alpha).$$ We set it equal to $0$ and conclude: $$D'(\alpha)=0\ \Longrightarrow\ \cos^2\alpha=\sin^2\alpha\ \Longrightarrow\ \cos\alpha=\sin\alpha\ \Longrightarrow\ \alpha=\frac{\pi}{4}.$$ $\square$
Exercise. Use a trigonometric formula to finish the solution without differentiation.
Exercise. What if we shoot from a hill?
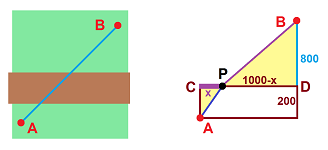
Example (laying a pipe). Suppose we are to lay a pipe from point $A$ to point $B$ located one kilometer east and one kilometer north of $A$. The cost of laying a pipe is normally $\$50$ per meter, except for a rocky strip of land $200$ meters wide that goes east-west; here the price is $\$100$ per meter. What is the lowest cost to lay this pipe?
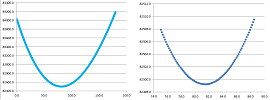
First we discover that it doesn't matter where the patch is located and assume that we have to cross it first. We proceed from $A$ to point $P$ on the other side of the patch and then to $B$. Then the cost $C$ is $$C=|AP|\cdot 100+|PB|\cdot 50.$$ We next denote by $x$ the distance from $P$ to the point directly across from $A$. Then $$|AP|=\sqrt{200^2+x^2} \text{ and } |PB|=\sqrt{(1000-x)^2+800^2}.$$ Therefore, we are to minimize the cost function: $$C(x)=\sqrt{200^2+x^2}\cdot 100+\sqrt{(1000-x)^2+800^2}\cdot 50.$$ Now, we convert this formula into a spreadsheet formula: $$\texttt{=sqrt(200^2+RC[-1]^2)*100+sqrt((1000-RC[-1])^2+800^2)*50.}$$ Plotting the curve, and then zooming in, suggests that the optimal choice for $x$ is about $81.5$ meters with the cost about $\$82,498.50$:
Let's confirm the result with calculus. Differentiate: $$\begin{array}{lll} C'(x)&=\left( \sqrt{200^2+x^2}\cdot 100+\sqrt{(1000-x)^2+800^2}\cdot 50\right)'\\ &=\frac{2x}{2\sqrt{200^2+x^2}}\cdot 100+\frac{-2(1000-x)}{2\sqrt{(1000-x)^2+800^2}}\cdot 50. \end{array}$$ The equation $C'(x)=0$ proves itself too complex to be solved exactly. Instead, we look back at the picture to recognize the terms in this expression as fractions of sides of these two triangles: $$C'(x)=\cos\widehat{APC}\cdot 100-\cos\widehat{BPD}\cdot 50.$$ Then, $C'=0$ if and only if $$\frac{\cos\widehat{APC}}{\cos\widehat{BPD}} =\frac{50}{100}.$$ In other words, the optimal price is reached when the ratio of the cosines of the two angles at $P$ are equal to the ratio of the two prices. In particular, making the price of laying the pipe across the patch more expensive will make this part of the path to cross more directly. Since cosine is a decreasing function on $(0,\pi/2)$, we conclude that $\widehat{BPD}$ is expressed uniquely in terms of $\widehat{APC}$. $\square$
Exercise. Show that, indeed, the location of the strip doesn't matter. Hint: geometry.
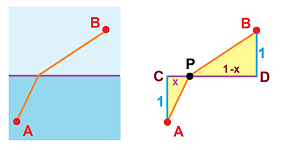
Example (refraction). Suppose light is passing from one medium to another. It is known that the speed of light through the first is $v_1$ and through the second $v_2$. We rely on the principle that light follows the path of fastest speed and find the angle of refraction. A similar but simpler set-up:
Let $x$ be the parameter, then the time it takes to get from $A$ to $B$ is: $$\begin{array}{lll} T(x)&= \frac{|AP|}{v_1}+\frac{|AP|}{v_2}\\ &= \frac{\sqrt{1+x^2}}{v_1}+\frac{\sqrt{1+(1-x)^2}}{v_2}. \end{array}$$ We differentiate just as in the last example: $$\begin{array}{lll} T'(x)&=\frac{1}{v_1}\frac{x}{\sqrt{1+x^2}}+\frac{1}{v_2}\frac{-(1-x)}{\sqrt{1+(1-x)^2}}\\ &=\frac{1}{v_1}\cos\widehat{APC}-\frac{1}{v_2}\cos\widehat{BPD}. \end{array}$$ And $T'=0$ if and only if $$\frac{\cos\widehat{APC}}{\cos\widehat{BPD}} =\frac{v_1}{v_2}.$$ Therefore, light follows the path with the ratio of the cosines of the two angles at $P$ equal to the ratio of the two propagation speeds. $\square$
Exercise. Find the distance from the point $(1,1)$ to the parabola $y=-x^2$ by two methods: (a) find the minimal distance between the point and the curve, and (b) find the line perpendicular to the curve and its length.
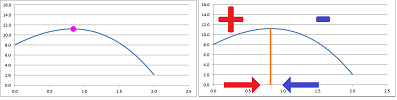
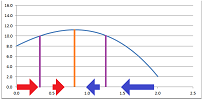
Example (numerical optimization). The differentiation might produce a function so complex that solving the equation $f'=0$ analytically is impossible. In that case we can apply one of the iterative processes of solving equation discussed earlier in this chapter. Alternatively, we design a process that follows the direction of the derivative as it always points at the nearest maximum.
In other words, we move along the $x$-axis and
- we step right when $f'>0$, and
- we step left when $f'<0$.
We reverse the direction when we look for a minimum. We make a step proportional to the derivative so that its magnitude also matters; we move faster when it's higher.
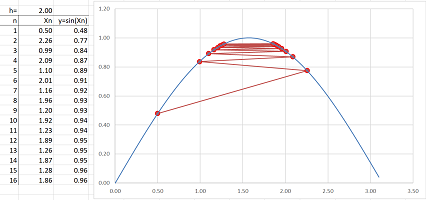
As you can see, the motion will slow down as we are get closer to the destination, which is convenient. So, we build a sequence of approximations recursively: $$x_{n+1}=x_n+h\cdot f'(x_n),$$ where $h$ is the coefficient of proportionality. For example, for $f(x)=\sin x$, we have $$x_{n+1}=x_n+h\cdot \cos(x_n).$$ The spreadsheet formula is: $$\texttt{=R[-1]C+R2C*COS(R[-1]C)}.$$
Especially for functions of several variables (Chapter 18), the method is called the gradient descent or ascent. $\square$
Example (line fitting). What is the best linear approximation of a sequence of points? The idea is to minimize the sum of the distances -- vertical distances -- from the line to the points.
In other words, if we have a sequence of $n$ points on the plane: $$(x_1,y_1),(x_2,y_2),...,(x_n,y_n),$$ we are to find such number $m$ (the slope) that the following function reaches its minimum: $$R(m)=\sum_{k=1}^n|mx_k-y_k|.$$ We suddenly realize that this function is non-differentiable and, therefore, none of the method that we have available applies!
$\square$