Triangulations of surfaces

Redirect to:

• Manifolds#Manifolds and manifolds with boundary

Recall that every point in a surface (without boundary) has a neighborhood homeomorphic to ${\bf R}^2$.

Suppose we have a $2$-dimensional simplicial complex $K$. How do we know that the realization of $K$ is a surface?

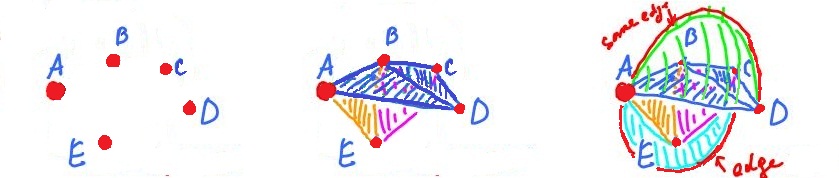
For example, consider of the complex $$ABD, BCD, ACD, ABE, BCE, ACE.$$ If we start attaching cells to each other:

we discover that its realization is homeomorphic to the sphere.

Can we answer the question by examining the list of simplices? The answer is Yes.

The first requirement a complex has to satisfy to be a surface is:

• (a) each edge is shared by exactly two faces.

This condition can fail in two ways:

1. an edge is contained in exactly one face,
2. an edge is shared by more than two faces.

In the first case we have, possibly, a surface with boundary. In the second, a point on this edge does not have a neighborhood homeomorphic to the disk.

Now, how do we restate this condition combinatorially for a given simplicial complex $K$ given by a list of subsets of ${A,B,C,...}$?

In terms of sets, every face is a triple, such as $ABC$, and every edge is a double, such as $AB$. Condition (a) can then be restated in term of subsets of ${A,B,C,...}$ as:

• (A) if $AB∈K$ then there are exactly two $C,D∈K$ satisfying

$$ABC, ABD∈K.$$

This condition does not guarantee that the realization of $K$ is a surface, as the image below shows.

Indeed, condition (A) is satisfied here but the vertex in the middle does not have a neighborhood homeomorphic to the disk.

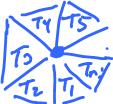
Then, we have to require that the faces around each vertex are arranged in a circular fashion to form a disk-like surface.

Given a vertex $A$ the faces (triangles) that contain $A$ have to form a "cycle":

$T_0$ glued to $T_1$ glued to $T_2$ ... $T_n$ glued to $T_0$.

We can state this as a condition on faces:

• (b) for each vertex $A$, if
  • all edges that contain $A$ are $E_0, E_1, ..., E_n$ and
  • all triangles that contain $A$ are $T_0, T_1, ..., T_n$,
• then they can be re-indexed in such a way that:
  • $E_0$ is shared by $T_0, T_1$;
  • $E_2$ is shared by $T_1, T_2$;
  • ...
  • $E_n$ is shared by $T_n, T_0$.

Note: This collection of simplices is called the star of vertex $A$. For a related construction see Nerve of cover.

Restated in terms of subsets of ${A, B, C, ...}$, condition (b) will take the following form:

• (B) for each $A∈K$, the set ${B∈K: AB∈K}$ can be represented as ${B_0, B_1, ..., B_n}$ with

$$AB_0B_1, AB_1B_2, ..., AB_nB_0∈K.$$

Theorem. If a simplicial complex $K$ satisfies conditions (A) and (B) then its realization $|K|$ is a surface.