This site is being phased out.
Quotients of manifolds
Redirect to:
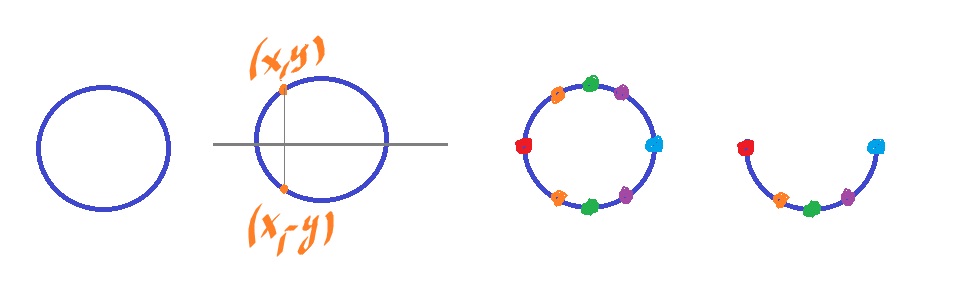
Example. Let consider the quotient of the circle ${\bf S}^1/_{\sim}$ with two different equivalence relations. The circle has neighborhoods of each point homeomorphic to ${\bf R}$, i.e., it's a $1$-dimensional manifold. Now we want to see the effect of gluing on its structure.
Suppose the circle is centered at $0$ on the $xy$-plane.
Firstly, suppose $$(x,y) \sim (x,-y).$$
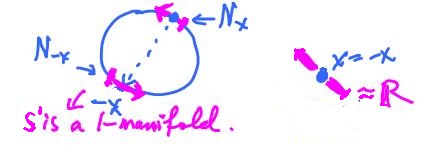
In other words, each point is identified with the one symmetric with respect to the $x$-axis. Then $$X = {\bf S}^1/_{\sim} $$ is not a $1$-manifold because $(1,0)$ and $(-1,0)$ don't have neighborhoods homeomorphic to ${\bf R}$ anymore. Indeed, they are homeomorphic to the ray ${\bf R}^+$.
In fact, $X$ is simply the half circle: $${\bf S}^1/_{\sim} = {\bf I} = [0,1].$$
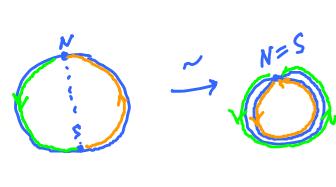
Example. Secondly, suppose $$(x,y) \sim (-x,-y). $$
In other words, each point is identified with the one symmetric with respect the origin (the antipodal point). Then $X = {\bf S}^1/_{\sim}$ is still a $1$-manifold as the image shows.
What is it? It's another circle: $${\bf S}^1/_{\sim} = {\bf S}^1.$$
Exercise. Consider this kind of antipodal equivalence relation for the spheres ${\bf S}^2/_{\sim}$, ..., ${\bf S}^n/_{\sim}$ with $x \sim -x$.
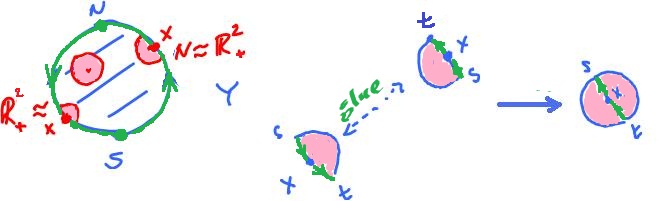
Example. Next, let's consider a certain quotient of the disk: $$Y = {\bf B}^2/_{\sim}.$$
First, observe that $${\partial}{\bf B}^2 = {\bf S}_1,$$ therefore the identification considered above applies:
In other words, the edge of the disk is glued to itself, with a twist.
Observe that even though the disk has a boundary, $Y$ is a surface without boundary. Indeed, a point $x$ on the edge has a neighborhood homeomorphic to half-disk but, when it's glued to its antipodal point, the two half-disks form a whole disk.
The end result is called the projective plane ${\bf P}^2$.
Why isn't it, say, the sphere? Because it contains the Mobius band:
Such surfaces are called one-sided, or non-orientable.
See also Examples of cell complexes and Connected sum.